Java应用实例:三角形判断(向量叉积、海伦公式)、分数序列求和
一、三角形判断
1.题目
在数学中,如果知道了三个点的坐标,我们就可以判断这三个点能否组成一个三角形;如果可以组成三角形,那么我们还可以求出这个三角形的面积。作为一个大学生,如果给你三个点的坐标,你能快速判断出这三个点能组成一个三角形吗?如果可以组成三角形,你能快速求出三角形的面积吗?
要求:第一行输入一个整数N(1 ≤ N ≤ 100),表示有N组测试数据。
接下来有N行,每行包括六个数x1,y1,x2,y2,x3,y3,分别代表三个点的坐标(可能是小数)。
(0 ≤ x1,y1,x2,y2,x3,y3 ≤ 15)
根据点的坐标判断这三个点能不能组成一个三角形,如果可以组成三角形,输出这个三角形的面积,结果保留3位小数;否则,输出“ Can not form a triangle.”。
2.题解
这里就略过输入等基础操作了,主要讲解算法方面
1)方法一(向量叉积公式)
假设我们有三角形的三个顶点:
-
A(x₁, y₁)
-
B(x₂, y₂)
-
C(x₃, y₃)
步骤1:构造两个边向量
从同一个顶点出发,构造两个边向量:
-
向量 AB = (x₂ - x₁, y₂ - y₁)
-
向量 AC = (x₃ - x₁, y₃ - y₁)
步骤2:计算叉积
AB × AC = (x₂ - x₁)(y₃ - y₁) - (y₂ - y₁)(x₃ - x₁)步骤3:取绝对值并除以2
由于叉积给出的是平行四边形的面积,而三角形是平行四边形的一半:
三角形面积 = |AB × AC| / 2*步骤4:展开公式
将叉积公式展开并整理,得到常用的三角形面积公式:
面积 = |x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)| / 2实际计算示例
假设三角形顶点为:
-
A(0, 0)
-
B(4, 0)
-
C(0, 3)
计算过程:
-
构造向量:
-
AB = (4-0, 0-0) = (4, 0)
-
AC = (0-0, 3-0) = (0, 3)
-
-
计算叉积:
-
AB × AC = 4×3 - 0×0 = 12
-
-
计算面积:
-
面积 = |12| / 2 = 6
-
这正是直角边长为3和4的直角三角形的正确面积(3×4/2=6)。
代码实现
double s = Math.abs((x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)) / 2.0);2)海伦公式
假设在平面内有一个三角形,三边边长分别为a、b、c,则SΔ可由三边的边长求得
海伦公式表述为:
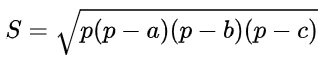
其中p为半周长(三角形周长的一半):
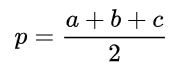
在《度量论》(Metrica)手抄本中用作为半周长,所以三角形面积也可表示为:
实际情况中p多用作为半周长。
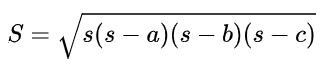
秦九韶公式表述为:
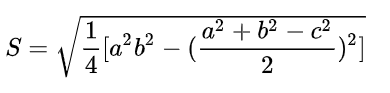
海伦公式和秦九韶公式本质是一样的,两个公式可相互转换,因此通常称海伦公式为海伦-秦九韶公式。
代码实现
// 使用海伦公式计算面积double p = (arr[0] + arr[1] + arr[2]) / 2; // 半周长double s = Math.sqrt(p * (p - arr[0]) * (p - arr[1]) * (p - arr[2]));3.完整代码
1)方法一(向量叉积公式)
import java.util.Scanner;
import java.util.Arrays;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt();double[] arr = new double[3];for (int i = 0; i < N; i++) {double x1 = sc.nextDouble();double y1 = sc.nextDouble();double x2 = sc.nextDouble();double y2 = sc.nextDouble();double x3 = sc.nextDouble();double y3 = sc.nextDouble();arr[0] = Math.sqrt(Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2));arr[1] = Math.sqrt(Math.pow(x1 - x3, 2) + Math.pow(y1 - y3, 2));arr[2] = Math.sqrt(Math.pow(x2 - x3, 2) + Math.pow(y2 - y3, 2));Arrays.sort(arr);if (arr[0] + arr[1] <= arr[2]) {System.out.println("Can not form a triangle.");} else {double s = Math.abs((x1*(y2-y3) + x2*(y3-y1) + x3*(y1-y2)) / 2.0);System.out.printf("%.3f\n", s);}}}
}2)方法二(海伦公式)
import java.util.Scanner;
import java.util.Arrays;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt();double[] arr = new double[3];for (int i = 0; i < N; i++) {double x1 = sc.nextDouble();double y1 = sc.nextDouble();double x2 = sc.nextDouble();double y2 = sc.nextDouble();double x3 = sc.nextDouble();double y3 = sc.nextDouble();// 计算三边长度arr[0] = Math.sqrt(Math.pow(x1 - x2, 2) + Math.pow(y1 - y2, 2));arr[1] = Math.sqrt(Math.pow(x1 - x3, 2) + Math.pow(y1 - y3, 2));arr[2] = Math.sqrt(Math.pow(x2 - x3, 2) + Math.pow(y2 - y3, 2));Arrays.sort(arr);if (arr[0] + arr[1] <= arr[2]) {System.out.println("Can not form a triangle.");} else {// 使用海伦公式计算面积double p = (arr[0] + arr[1] + arr[2]) / 2; // 半周长double s = Math.sqrt(p * (p - arr[0]) * (p - arr[1]) * (p - arr[2]));System.out.printf("%.3f\n", s);}}}
}二、分数序列求和
1.题目
有一分数序列: 2/1、3/2、5/3、8/5、13/8、21/13…
求出这个数列的前N项之和,保留两位小数。
要求:输入为一行,输入正整数N。(1<N<=1000)
输出为一行,输出数列前N项和,保留2位小数。
2.题解
-
输入处理:使用
Scanner读取输入的整数N,表示需要计算的项数。 -
初始化变量:
a和b分别初始化为2.0和1.0,代表序列第一项的分子和分母。sum初始化为0,用于累加各项的和。 -
循环计算:通过循环N次,每次计算当前项的值
a/b并累加到sum中。然后更新分子a为a + b,分母b为原来的分子a,为下一次迭代做准备。 -
输出结果:使用
printf格式化输出结果,保留两位小数。
3.完整代码
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int N = scanner.nextInt();double sum = 0;double a = 2.0; // 分子double b = 1.0; // 分母for (int i = 0; i < N; i++) {sum += a / b;double nextA = a + b;double nextB = a;a = nextA;b = nextB;}System.out.printf("%.2f", sum);}
}