概率统计中的数学语言与术语1

概率统计里有一套非常专门的数学语言和术语，如果你是初学者，很容易被符号和定义绕晕。按常见分类整理一下，方便理解和记忆：

---

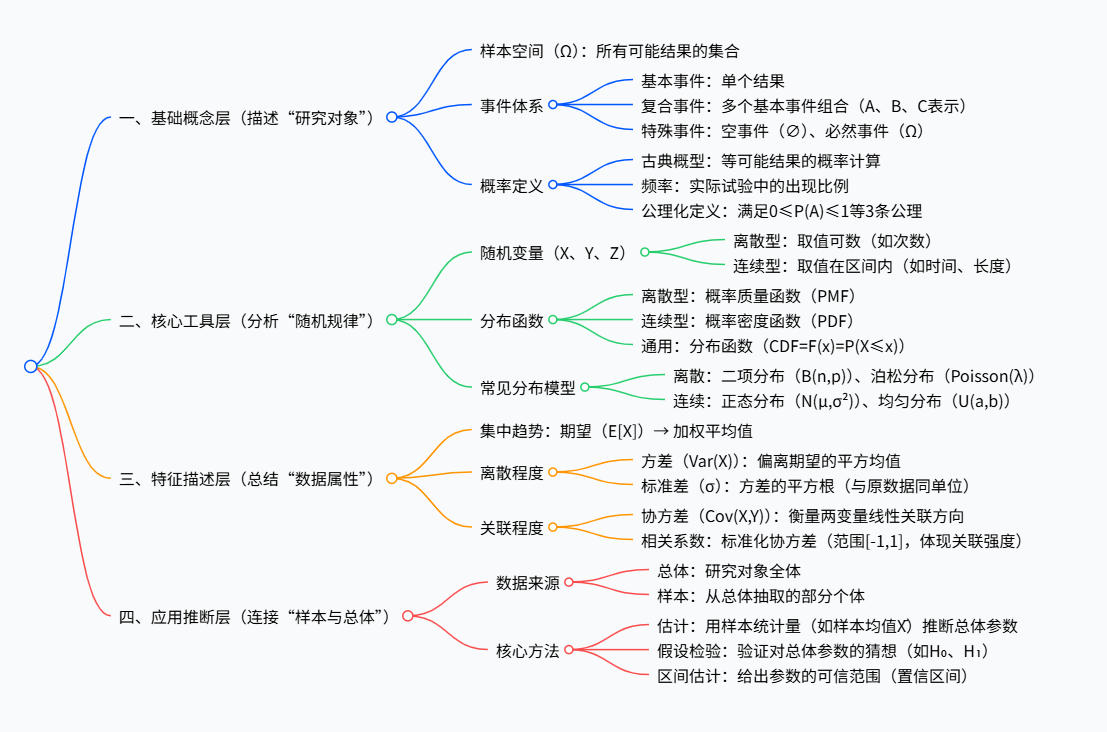
一、基础集合与事件语言

• 样本空间（Sample Space）：所有可能结果的集合，记作 $\Omega$。
• 事件（Event）：样本空间的子集，常用大写字母 $A,B,C$ 表示。
• 基本事件（Elementary Event）：只包含一个结果的事件。
• 空事件（Impossible Event）：记作 $\varnothing$，不可能发生的事件。
• 必然事件（Certain Event）：记作 $\Omega$，一定会发生的事件。

---

二、概率的基本概念

• 概率（Probability）：事件发生的可能性大小，记作 $P(A)$，满足 $0\le P(A)\le 1$。
• 古典概型（Classical Probability）：所有基本事件等可能发生的概率模型。
• 频率（Frequency）：在多次重复试验中事件出现的次数比例。
• 条件概率（Conditional Probability）：在已知事件 $B$ 发生的条件下，事件 $A$ 发生的概率，记作 $P(A|B)$。
• 独立性（Independence）：若 $P(A\cap B)=P(A)P(B)$，则称事件 $A$ 与 $B$ 独立。

---

三、随机变量与分布

• 随机变量（Random Variable）：把样本空间的结果映射为实数的函数，常用大写字母 $X,Y,Z$ 表示。
• 离散型随机变量（Discrete Random Variable）：取值有限或可数的随机变量。
• 连续型随机变量（Continuous Random Variable）：取值充满某个区间的随机变量。
• 概率分布（Probability Distribution）：描述随机变量取值概率规律的函数。
• 离散型：概率质量函数（PMF）
• 连续型：概率密度函数（PDF）
• 分布函数（CDF）：$F(x)=P(X\le x)$，表示随机变量小于等于 $x$ 的概率。

---

四、常见分布名称

• 离散分布：二项分布 $B(n,p)$、泊松分布 $\text{Poisson}(\lambda )$、几何分布等。
• 连续分布：正态分布 $N(\mu ,{\sigma }^2)$、均匀分布 $U(a,b)$、指数分布 $\text{Exp}(\lambda )$、伽马分布等。

---

五、期望、方差与矩

• 期望（Expected Value）：随机变量的加权平均值，记作 $E[X]$。
• 方差（Variance）：衡量随机变量取值分散程度，记作 $\text{Var}(X)$。
• 标准差（Standard Deviation）：方差的平方根，记作 $\sigma$。
• 协方差（Covariance）：衡量两个随机变量的线性关系程度，记作 $\text{Cov}(X,Y)$。
• 相关系数（Correlation Coefficient）：标准化的协方差，范围 $[-1,1]$。

---

六、统计推断常用术语

• 总体（Population）：研究对象的全体。
• 样本（Sample）：从总体中抽取的部分个体。
• 统计量（Statistic）：由样本计算出的量，如样本均值 $\bar{X}$、样本方差 $S^2$。
• 估计（Estimation）：用样本统计量推断总体参数。
• 假设检验（Hypothesis Testing）：对总体参数提出假设并进行检验。
• 置信区间（Confidence Interval）：参数真值可能落入的区间估计。

---

• 置信区间（Confidence Interval）：参数真值可能落入的区间估计。

---