AI 基础知识二 神经网络概述
加权求和
经过之前的学习基本上知道神经网络是如何计算的,神经网络结构如图
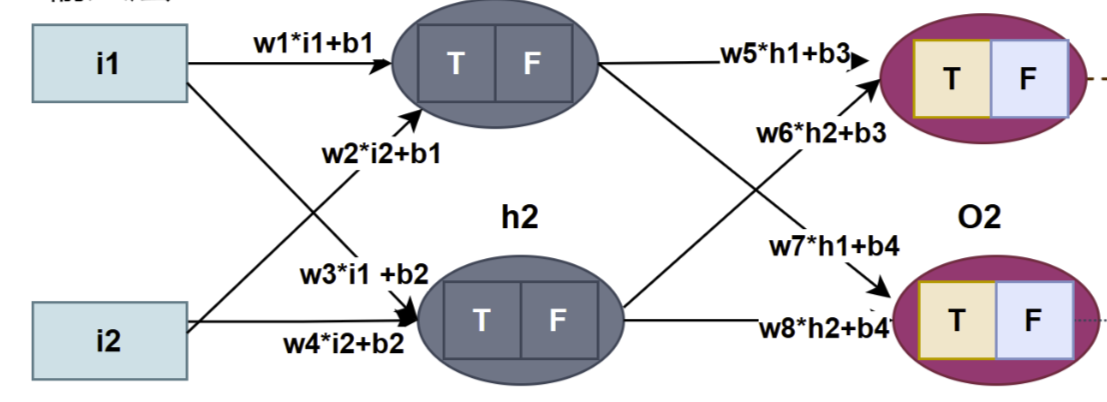
假如现在要在隐藏层增加两个神经元,程序中要增加8个权重(4个连输入层和4个连输出层)和2 个偏置量,这时要追加10个变量代码变得不易理解和维护,可见这不是一个好的程序设计,从数学公式上看也不够简洁。神经网络结构按层为单位,分析总结一下:每层至少有一个神经元,每个神经元有一个值(经过激活函数)和多个关连的权重(与上一层所有神经元连接的权重),每层神经元的值用一维数组存储(向量),偏置量也用一维数组存储(向量),权重用二维数组存储(矩阵) ,神经网络结构公式:
σ 为激活函数,神经元的值
神经元加权求和结果
权重矩阵,
上一层神经元的向量,
偏置量
轱辘输入层没有连接权重,所以从隐藏层开始那么它的加权求和数学表达示 或
如果隐藏层有4个四神经元它数学表达示
同理 可以推出输出层的数学表达示,神经网络的加权求和计算问题就可以转换为线性代数计算问题,把每层所有神经元当成一个向量,然后乘以矩阵的得到一个新的向量,向量乘以矩阵它的几何意义是对向量做某种变换(如平移、缩放、旋转)。
如对向量、矩阵运算 还不清楚的,或可参考DirectX12(D3D12)基础教程三 线性代数与3D世界空间_3d线性代数-CSDN博客
常见的激活函数
| 函数名称 | 输出范围 | 应用场景 | 优点 | 缺点 |
| Sigmoid | (0,1) | 1. 二分类问题 2. 概率值预测 3.通常用于输出层 | 1. 将值压缩到(0,1) 2. 适合概率输出 | 1.梯度消失问题 2.不适合深层网络 |
| Tanh 双曲正切函数 | (-1,1) | 中间隐藏层 | 1.输出值范围中心化在 0 附近 2.适合深度网络 | 1.极端值梯度消失 |
| ReLU 线性修正单元 | [0, | 隐藏层(卷积神经网络) | 1. 计算简单,收敛速度快 2 . 免了梯度消失 | 1.死亡神经元问题,输入为负值,其梯度始终为0 |
| Softmax | (0,1)且所有输出加和为1 | 多分类问题的输出层 | 1将输入值转化为概率分布,适合分类问题 | 对大输入值可能不稳定,需要归一化 |
| ELU | (−α,∞) | 隐藏层 | 解决ReLU神经元死亡问题 | |
| Swish | (−∞,∞) | 深层网络 | 平滑性较好,收敛速度快 | 计算稍复杂 |
| GELU高斯误差线性单元 | (−∞,∞) | Transformer 和 NLP 模型 | 1.表现平滑,计算效率高。 2.对小值保留小梯度,大值快速激活 | 计算复杂度高,实现复杂 |
| Maxout | (−∞,∞) | 高级模型的隐藏层 | 增加了模型的表达能力 | 参数较多,容易过拟合 |
常见的损失函数
| 函数名称 | 功能说明/应用场景 |
| CrossEntropyLoss交叉熵损失 | 多类别分类 、图像分类任务 |
| HingeLoss | 用于分类任务的损失函数,尤其在支持向量机(SVM)中被广泛应用,它的核心思想是最大化分类间隔,对正确分类且远离决策边界的样本惩罚较小,对错误分类或接近决策边界的样本惩罚较大。 |
| FocalLoss焦点损失 | 是为解决类别不平衡问题而设计的损失函数,尤其在目标检测等领域表现优异。它通过对交叉熵损失进行改进,降低了易分类样本的权重,聚焦于难分类样本(如稀有类别、模糊目标、小目标等),从而提升模型对少数类别的识别能力。 |
| KullbackLeiblerDivergence(KL 散度,也称为相对熵) | 概率模型评估与选择 |
| MSE, L2 Loss 均方误差 | 回归任务中最常用的损失函数之一。它通过计算模型预测值与真实值之间差值的平方的平均值来衡量预测误差。 |
| MAE, L1 Loss 平均绝对误差 | 回归任务中核心的损失函数之一,通过计算模型预测值与真实值之间绝对差值的平均值来衡量预测误差,对异常值的敏感度低于 MSE(L2 损失) |
| Huber Loss 胡贝尔损失 | 是一种结合了 MAE(L1 损失)和 MSE(L2 损失)优点的损失函数,它在误差较小时表现类似 MSE(平方误差),在误差较大时表现类似 MAE(绝对误差),从而兼顾了稳健性(对异常值不敏感)和优化效率(梯度平滑)。 |
| Quantile Loss分位数损失 | 预测区间(可能的最小值” 和 “可能的最大值”) |
| Dice Loss骰子损失 | 最初用于医学影像分割任务,尤其擅长处理类别极度不平衡的场景。它通过衡量预测结果与真实标签之间的重叠程度来计算损失,对小目标和稀疏类别更为敏感。 |
学习率
学习率(Learning Rate,简称 LR)是机器学习和深度学习中最关键的超参数之一,它控制模型在训练过程中通过梯度下降更新参数时的 “步长”。学习率的本质是在 “快速探索参数空间” 和 “精准逼近最优解” 之间寻找平衡,步长过大,可能跳过损失函数的局部最小值或全局最优解。步长过小,参数更新缓慢,训练收敛速度极慢,可能在有限迭代次数内无法达到最优解。常见学习率设置策略:
1.固定学习率
2.学习率衰减,前期快更,后期微调
3. 自适应学习率优化器,不依赖人工预设衰减规则,动态调整每个参数的学习率
4.循环学习率, 学习率在预设的 “最小值” 和 “最大值” 之间周期性波动
训练
若训练集包含 1000 个样本,模型逐一对这 1000 个样本进行了前向计算和反向传播,称为一个Epoch(轮次),假如1000 个样本无法一次性全部输入模型(受内存 / 显存限制),因此将数据集分割成若干个小部分,每个小部分称为一个 Batch(批次样本),如每批 按100 个样本分割,则可分成 10 个 Batch(相对于Iteration它是静态),Batch size(批次大小)是100。
模型每处理一个 Batch 的数据,并完成一次参数更新(前向计算 + 反向传播 + 梯度下降),称为一次 Iteration(迭代)(数值上与Batch相等,相对于Batch它是动态过程)。
总结
其实第一章用代码实现了一神经网络的核心功能,本章补充一些概念,总结一下训练神经网络模型过程是
1.前向计算传播
1.1加权求和
2.2激活函数
2.3向下一层传送,直到输出层
2. 计算损失函数
3. 反向传播,设置学习率策略,梯度下降
目前我们用代码实现一个简单样例,如果网络层数增多、更换算法,再比如需要硬件加速计算(GPU)等等,从0开始实现是一件低效率的事,因此要寻找到好用的开源库。
PyTorch 是由 Meta(原 Facebook)开发的一款开源深度学习框架,以其动态计算图、简洁易用的 API ,尤其在学术研究和快速原型开发中应用广泛。 PyTorch框架主流开发语言是python,容易上手。不过这里介绍c++加 libtorch的使用,下一章讲解libtorch环境配置和使用libtorch构建上一章的神经网络。
感谢大家的支持,如要问题欢迎提问指正。
