CS50ai: week2 Uncertainty我的笔记B版——当 AI 开始“承认不确定”
前言:当 AI 开始“承认不确定”
我们总想让 AI 像数学证明一样给出“确定”的答案,可现实世界处处充满不确定:传感器有噪声、天气会变脸、骰子看心情。于是,概率登场了。它允许我们“在不确定里做确定的事”——用数字表达“有多大可能”,再用推理把这些可能性转成可靠判断。本篇带你从零走到能看懂贝叶斯网络与隐马尔可夫模型(HMM)的入门级实战思维。保证好懂,偶尔俏皮,但公式绝不含糊。
一、概率的“可能世界”视角
- 可能世界 Ω 与事件 ω
- 把一次随机过程(掷骰子、明天下雨与否)看作从“所有可能世界”Ω 中挑一个世界 ω。
- 基本公理:
- 0≤P(ω)≤10≤P(ω)≤1
- ∑ω∈ΩP(ω)=1∑ω∈ΩP(ω)=1
这俩公理是“概率不会超界,所有可能性加总必为 1”的数学化表达。
二、无条件概率与条件概率:知道与“已知”
- 无条件概率(unconditional):没有任何证据时的信念程度。
- 条件概率(conditional):在已知证据 b 的前提下,a 成立的概率。
- 记法:P(a∣b)P(a∣b),“a given b”
- 定义与等价式:
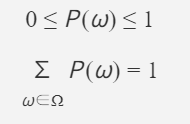
一句人话:在 b 的世界里,a 占的比例,就是 P(a∣b)P(a∣b)。
三、随机变量与概率分布:把“可能状态”列表化
- 随机变量(Random Variable):变量的取值来自一个离散集合(域)。
- 例:Weather ∈ {sun, cloud, rain, wind, snow}
- 例:Flight ∈ {on time, delayed, cancelled}
- 概率分布:给每个可能值一个概率:
- 例:Flight 的分布
- P(on time)=0.6P(on time)=0.6, P(delayed)=0.3P(delayed)=0.3, P(cancelled)=0.1P(cancelled)=0.1
- 向量记法:P(Flight)=⟨0.6,0.3,0.1⟩P(Flight)=⟨0.6,0.3,0.1⟩(顺序很重要)
四、独立与“不独立”:别把“云”和“雨”当陌生人
- 独立(Independence):知道一个事件发生,不改变另一个的概率。
- 若独立:
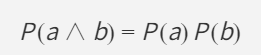
- 骰子红蓝两颗是独立的;“多云”和“下雨”显然常常不是独立。
独立≠永远,建模要靠常识与数据判断。
五、贝叶斯公式:交换条件的魔法
- 贝叶斯规则:
P(b∣a)=P(a∣b)P(b)/P(a)
- 小例子(“早上多云→下午下雨?”):
- 已知:80% 的“下午下雨”日有“早上多云”;40% 天“早上多云”;10% 天“下午下雨”。
- 直觉翻译:知道“效应|原因”,就能算“原因|效应”。医学检测、欺诈识别常用这招。
六、联合概率与常用规则:四个“口袋公式”
- 联合概率:多个事件同时发生的概率,写作 P(a,b)P(a,b) 或 P(a∧b)P(a∧b)。
- 否定:P(¬a)=1−P(a)P(¬a)=1−P(a)
- 容斥(并集):P(a∨b)=P(a)+P(b)−P(a∧b)P(a∨b)=P(a)+P(b)−P(a∧b)
- 边缘化(求和外变量):
- 二元布尔版:P(a)=P(a,b)+P(a,¬b)P(a)=P(a,b)+P(a,¬b)
- 多值版:对另一个随机变量的所有取值求和。
- 条件化:P(a)=P(a∣b)P(b)+P(a∣¬b)P(¬b)P(a)=P(a∣b)P(b)+P(a∣¬b)P(¬b)
这些是做题“随手掏”的工具箱。
七、从“联合变条件”:比例与归一化的技巧
当我们要算 P(C∣rain)P(C∣rain),常用“成比例再归一化”的办法:
P(C∣rain)=αP(C,rain)P(C∣rain)=αP(C,rain)

若已知 P(C,rain)=⟨0.08,0.02⟩P(C,rain)=⟨0.08,0.02⟩(对应“多云/不多云”),把它按比例缩放到和为 1:
α⟨0.08,0.02⟩=⟨0.8,0.2⟩α⟨0.08,0.02⟩=⟨0.8,0.2⟩
这就是“先算分子,再除以分母”的简写法(分母是常数,最后统一归一化)。
八、贝叶斯网络:把依赖“画出来”
- 定义:一种有向图结构,节点是随机变量,边表示依赖;每个节点有局部分布:
P(X∣Parents(X))P(X∣Parents(X))
- 直观理解:父节点像“原因”,孩子像“结果”。只需给出每个节点“看着父母”的条件分布,整个网络的联合分布就确定了。
- 计算联合概率(例):
P(Appointment | light, no) = α * P(Appointment, light, no)
P(Appointment, light, no) = P(Appointment, light, no, on time) + P(Appointment, light, no, delayed)
等于四个节点各自“看着父母”的概率连乘。
- 枚举推断(Inference by Enumeration):
P(X∣e)=α∑yP(X,e,y)P(X∣e)=αy∑P(X,e,y)
- X:查询变量;e:已知证据;y:所有隐藏变量的取值组合;α:归一化常数。
- 一句话:把未知的都“枚举求和”,把已知的“代进去”,最后“归一化”。
小提示:实际工程里会用库(如 pomegranate)构图、填表、做推断,避免手算崩溃。
九、近似推断:不会“精确”,那就“足够好”
当网络变大、变量变多,精确枚举就吃不消了。采样来救场。
- 直接采样(Prior Sampling):按拓扑序,从根到叶“按条件分布抽签”,得到一个完整样本。抽很多次,用样本频率近似概率。
- 拒绝采样(Rejection Sampling):只保留与证据匹配的样本,不匹配就丢掉。证据稀有时效率很低(丢太多)。
- 似然加权(Likelihood Weighting):
- 固定证据变量(不再抽它们)。
- 对非证据变量继续条件采样。
- 每个样本赋权重 = “证据出现的似然”(对应条件表里的概率)。
- 用“带权频率”估计目标分布。比拒绝采样稳很多。
选型口诀:证据稀有 → 少用拒绝采样;想稳妥 → 试试似然加权。
十、马尔可夫假设与马尔可夫链:时间上的“只记昨天”
- 马尔可夫假设:当前状态只依赖有限个前态(最常用:只依赖“上一时刻”)。
- 马尔可夫链(MC):满足马尔可夫假设的一串状态变量:
- 转移模型(例如天气):
- 若今天晴,明天晴 0.80.8,明天雨 0.20.2
- 若今天雨,明天雨 0.70.7,明天晴 0.30.3
- 你可以用它来“滚动预测”未来若干步,或做长期行为分析。
十一、传感器模型与隐马尔可夫模型(HMM)
现实中,真实状态常常“看不见”(hidden),我们只有“能观测”的信号(observation)。
- 传感器/发射模型(Emission):状态如何“产生”观测的概率。
- 例:若下雨,带伞概率高;若晴天,带伞概率低但不为 0。
- HMM = 马尔可夫链 + 发射模型:
- 上层:隐状态链(天气)按转移矩阵演化。
- 下层:每个隐状态“发射”一个观测(带伞/不带伞)。
- 经典任务(都基于条件概率的组合运算):
- Filtering:已观测到现在,求“当前状态分布”
- Prediction:已观测到现在,求“未来状态分布”
- Smoothing:已观测到现在,求“过去某时刻状态分布”
- Most Likely Explanation(Viterbi):给一串观测,求“最可能的状态序列”
思维要点:观测不是“真相”,但它与真相“有概率关系”。我们用这个关系“反推真相”。
十二、把它们串起来:从点到线,从静到动
- 静态世界:贝叶斯网络擅长建模“变量之间”的因果与依赖。
- 动态世界:马尔可夫链与 HMM 把“随时间变化”考虑进来,兼顾“不可见的真实状态”和“可见的观测”。
当你的问题“像一张网”,用贝叶斯网络;当你的问题“像一条时间线”,用马尔可夫链/HMM。遇到大模型或实时需求,用近似推断(采样)加速。
公式一览(收藏型)
- 0≤P(ω)≤10≤P(ω)≤1,∑ω∈ΩP(ω)=1∑ω∈ΩP(ω)=1
- 条件概率:P(a∣b)=P(a,b)P(b)P(a∣b)=P(b)P(a,b)
- 贝叶斯:P(b∣a)=P(a∣b)P(b)P(a)P(b∣a)=P(a)P(a∣b)P(b)
- 独立:P(a,b)=P(a)P(b)P(a,b)=P(a)P(b)
- 否定:P(¬a)=1−P(a)P(¬a)=1−P(a)
- 容斥:P(a∨b)=P(a)+P(b)−P(a,b)P(a∨b)=P(a)+P(b)−P(a,b)
- 边缘化:P(a)=∑bP(a,b)P(a)=∑bP(a,b)
- 条件化:P(a)=P(a∣b)P(b)+P(a∣¬b)P(¬b)P(a)=P(a∣b)P(b)+P(a∣¬b)P(¬b)
- 枚举推断:P(X∣e)=α∑yP(X,e,y)P(X∣e)=α∑yP(X,e,y)
- 采样派:直接采样 / 拒绝采样 / 似然加权
- 时间派:马尔可夫链(转移模型)、HMM(转移 + 发射)
结语:不确定中的“确定性工程”
AI 不需要“无所不知”才能靠谱,它需要的是:承认不确定 + 有据可依地计算不确定。本篇带你从概率公理、条件概率、贝叶斯法则,到贝叶斯网络、近似推断、马尔可夫链与 HMM,搭起一条从“静态推理”到“动态推理”的入门捷径。理解了这些,你就拿到了用概率驾驭现实世界的钥匙。
注意:该文章为ai根据cs50ai视频与我的笔记生成,因逻辑清晰且更具阅读性而发布,仅供学习参考
