排序算法汇总,堆排序,归并排序,冒泡排序,插入排序
215.数组中的第K个最大元素
1. 堆排序
复杂度分析:
- 建堆过程时间复杂度为O(n),堆排序过程时间复杂度为O(nlogn)

实现思路:
- 堆的排序过程实际上就是一颗完全二叉树,根据你输入的元素对该二叉树进行调整。以最小堆为例子,最终实现的效果就是越靠近根节点(上层节点)的其值越小,越靠近叶子节点(下层节点)的其值越大。
- 如输入数组为[3,2,1,5,6,4]时,此时这个最小堆二叉树为
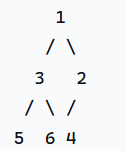
Code实现(使用python自带的堆进行实现)
import heapqclass Solution:def findKthLargest(self, nums: List[int], k: int) -> int:queue = []for ele in nums: ### 遍历过程:O(n)时间复杂度heapq.heappush(queue, ele) ### 排序过程:O(nlogn)时间复杂度result = []for _ in range(len(queue)):min_ele = heapq.heappop(queue)result.append(min_ele)return result[-k]2. 归并排序
复杂度分析:
- 归并排序是在递归的后序位置进行自底向上的排序,会有logn次的“并”,每次“并”的时间复杂度是O(n),所以整体时间复杂度为O(nlogn)
实现思路:
- 先划分再合并,类似的题目参考23. 合并 K 个升序链表,也是采用归并排序的做法
- 思路其实就是总-分-总,将大数组切割成小数组,当小数组长度为1时,此时就是最小数组单元。后续对两个最小数组单元进行排序,来得到一个稍微大点的有序数组,如此往复,就不断将多个有序数组进行合并后来得到整个的有序数组。
Code
class Solution:def findKthLargest(self, nums: List[int], k: int) -> int:result = self.merge_sort(nums)return result[-k]def merge_sort(self, nums): ### 分割数组if len(nums) <= 1:return numsmiddle = len(nums) // 2nums_left = nums[:middle]nums_right = nums[middle:]left = self.merge_sort(nums_left)right = self.merge_sort(nums_right)return self.merge(left, right) ## 左边和右边数组继续切割,切割完后进行merge操作def merge(self, nums_1, nums_2): ### 合并数组merge = []i=j=0while i < len(nums_1) and j < len(nums_2):if nums_1[i] <= nums_2[j]: ## nums_1 此时对比的元素更小merge.append(nums_1[i])i += 1else: ## nums_2 此时对比的元素更小 merge.append(nums_2[j])j += 1if i < len(nums_1):merge.extend(nums_1[i:])if j < len(nums_2):merge.extend(nums_2[j:])return merge3. 冒泡排序
复杂度分析:
-
最坏情况时间复杂度:O(n²),即每一次遍历元素都需要进冒泡; 最好情况时间复杂度:O(n),即每一次遍历时不需要进行冒泡,但需要对每个元素都进行遍历操作。平均情况时间复杂度:O(n²)
实现思路:
- 两个循环,一个循环对每个元素进行遍历。一个循环进行冒泡操作。
- 冒泡操作需要当前元素与下一个元素进行对比,如果当前元素 > 下一个元素,则两个元素需要交换。(相邻元素的判断 + 是否需要交换)
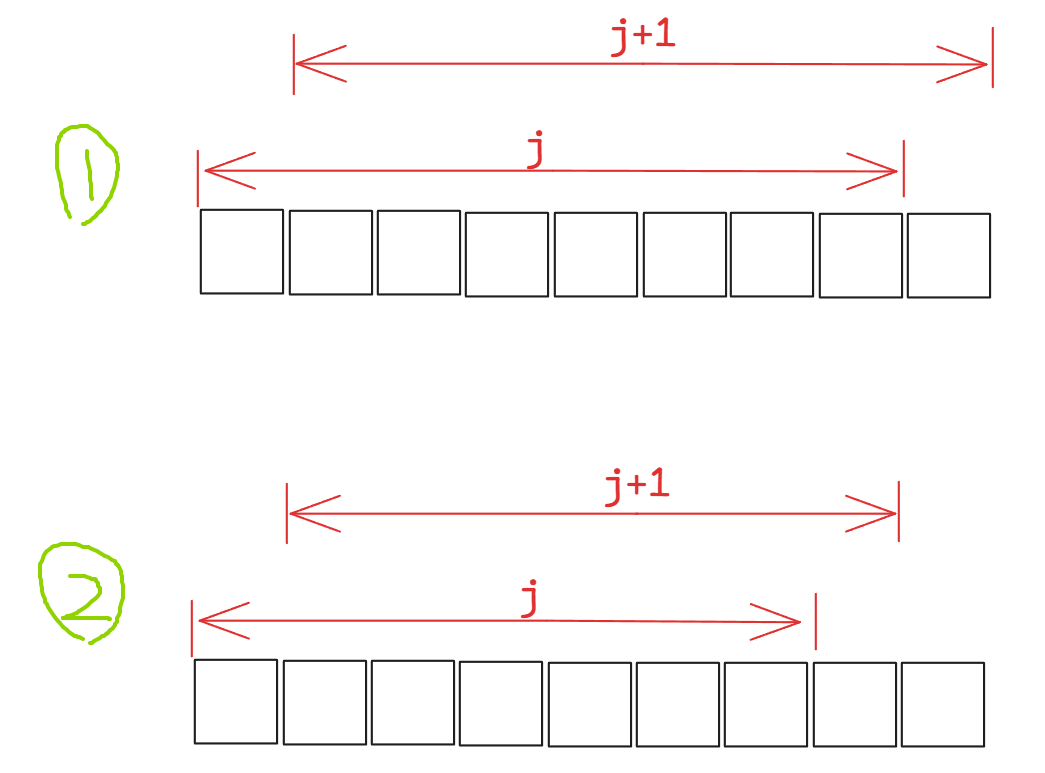
为什么第二个循环是length - 1 - i,为什么是length - 1 ,因为是跟下一个元素进行比较,因此这里是为了确保 j + 1不越界。而为什么还要减去 i 是因为每次冒后,后面的元素已经确定了,因此后续在进行冒泡时可以不用再比较这些元素了。如下,第一轮冒泡后最后一个元素已经确定是最大了,因此下一轮冒泡时就不用与最后一个元素进行比较了。
Code
class Solution:def findKthLargest(self, nums: List[int], k: int) -> int:result = self.bubble_sort(nums)return result[-k]def bubble_sort(self, nums):if len(nums) <= 1:return numslength = len(nums)for i in range(length): ### 确保每一个元素都经历了冒泡排序swapped = Falsefor j in range(length-1-i): ### 对每一个元素进行冒泡排序if nums[j] > nums[j+1]: ### 当前元素需要进行冒泡nums[j], nums[j+1] = nums[j+1], nums[j]swapped = True ### 记录有没有经过冒泡,表示当前数组还没排序好if not swapped: ### 如果swapped为False,表明不再需要进行冒泡了,数组已经排序好了breakreturn nums4. 插入排序
复杂度分析:
- 时间复杂度上:
- 最好情况:O(n) - 数组已经有序;最坏情况:O(n²) - 数组逆序,每次都要从头查找插入位置
- 平均情况:O(n²)
实现思路:
- 元素在插入到数组时,先与数组的最后一个元素对比,如果比这个元素大,那么就可以直接插入到数组的末尾处。
- 如果没比最后一个元素大,那就要重头开始进行判断操作,判断从左到右,数组中哪个元素刚好大于这个插入值,那就将插入值插入到这个位置,原本这个位置和这个位置之后的元素都同步右移一位。
Code
class Solution:def findKthLargest(self, nums: List[int], k: int) -> int:result = self.quick_sort(nums)return result[-k]def quick_sort(self, nums):if len(nums) <= 1:return numsresult = []for i in range(len(nums)):if not result:result.append(nums[i])else:pre_val = result[-1]cur_val = nums[i]if cur_val >= pre_val:result.append(cur_val)else:left = 0while result[left] < cur_val:left += 1result.insert(left, cur_val) ### 在result数组中的left下标添加cur_val这个元素return result