磁共振成像原理（理论）15：空间信息编码 (Spatial Information Encoding) -频率编码相位编码

在信号被选择性或非选择性射频脉冲激发后，空间信息可以在自由进动期间编码到信号中。由于激发的磁共振信号呈复指数形式，我们本质上可以通过两种方式编码空间信息：频率编码和相位编码。

频率编码

频率编码使激发的磁共振信号的振荡频率线性依赖于其空间位置。

考虑一个理想化的一维物体，其自旋分布为 $\rho (x)$。如果在激发后物体经历均匀主磁场 $B_0$ 叠加线性梯度场 $G_{x}x$，则位置 $x$ 处的拉莫尔频率为：
$$\omega (x)={\omega }_0+\gamma G_{x}x\text{\hspace{1em}(5.48)}$$

相应地，在点 $x$ 处无限小间隔 $dx$ 内的自旋产生的自由感应衰减信号（忽略横向弛豫效应）为：
$$dS(x,t)\propto \rho (x)dx{e}^{-i\gamma (B_0+G_{x}x)t}\text{\hspace{1em}(5.49)}$$

其中比例常数取决于翻转角、主磁场强度等因素。为简化符号，我们忽略这个缩放常数，将公式(5.49)重写为：
$$dS(x,t)=\rho (x)dx{e}^{-i\gamma (B_0+G_{x}x)t}\text{\hspace{1em}(5.50)}$$

公式(5.50)中的信号被称为频率编码信号，因为其振荡频率 $\omega (x)=\gamma (B_0+G_{x}x)$ 与空间位置线性相关。因此，在这个例子中，$G_x$ 被称为频率编码梯度。

$G_x$梯度场对磁共振信号频率的影响如下图所示：频率编码梯度场使得不同空间位置（$x$方向）的原子团具备不同的拉莫尔频率，随着时间的推进，这些信号逐渐失去相位一致性。因此，经过频率编码的接收信号预期将以比未编码信号更快的速率衰减。

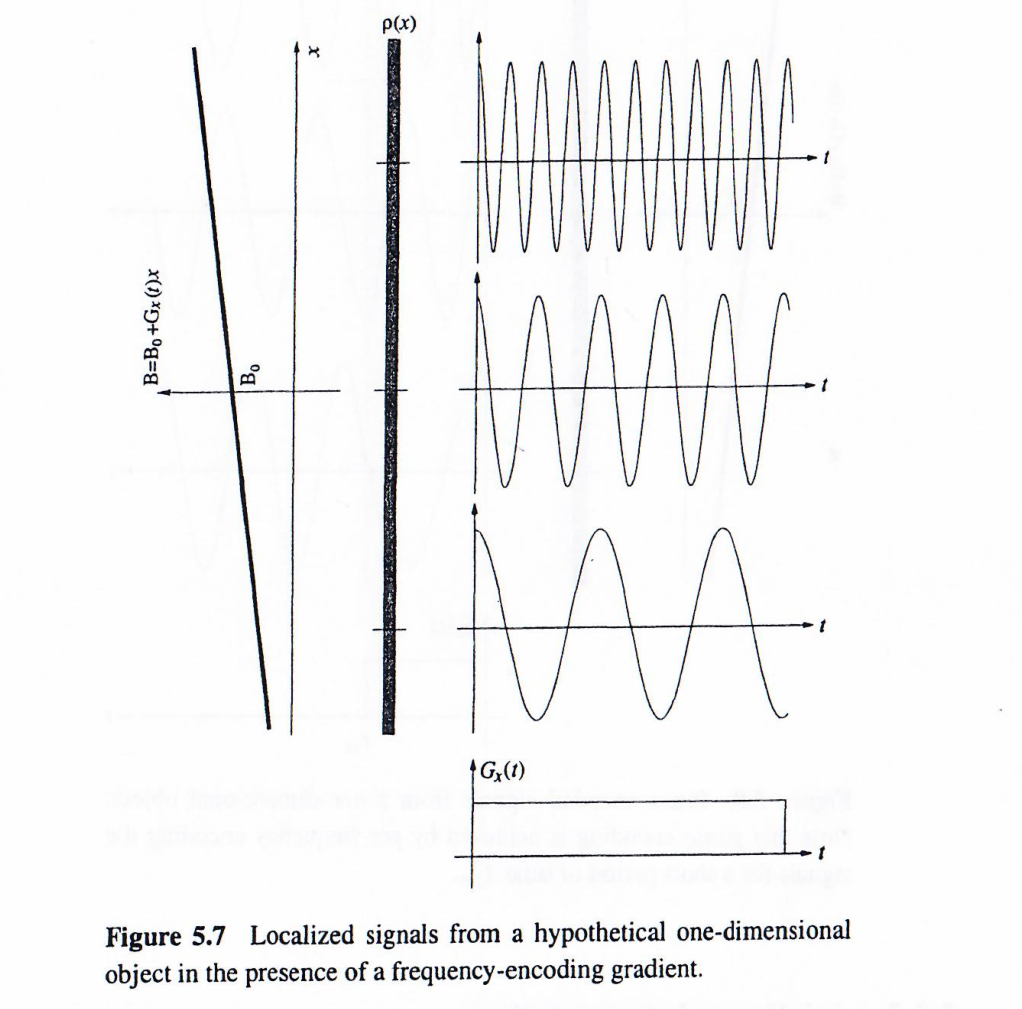
当存在此频率编码梯度时，从整个物体接收到的信号为：
$$\begin{array}{rl}S(t)={\int }_{\text{object}}dS(x,t)& ={\int }_{-\infty }^{\infty }\rho (x)e^{-i\gamma (B_0+G_{x}x)t}dx\\ & =[{\int }_{-\infty }^{\infty }\rho (x)e^{-i\gamma G_{x}xt}dx]e^{-i{\omega }_{0}t}\end{array}\text{\hspace{1em}(5.51)}$$

解调（即去除载波信号 $e^{-i{\omega }_{0}t}$）后，得到：
$$S(t)={\int }_{-\infty }^{\infty }\rho (x)e^{-i\gamma G_{x}xt}dx\text{\hspace{1em}(5.52)}$$

将分析推广到一般情况，解调后的频率编码自由感应衰减信号的一般表达式可表示为：
$$S(t)={\int }_{\text{object}}\rho (\mathbf{r})e^{-i\gamma {\mathbf{G}}_{\text{fe}}\cdot \mathbf{r}\cdot t}d\mathbf{r}\text{\hspace{1em}(5.53)}$$

其中 ${\mathbf{G}}_{\text{fe}}$ 是频率编码梯度（下标$fe$就是Frequency Encoding的缩写）定义为：

$${\mathbf{G}}_{\text{fe}}=(G_x,G_y,G_z)\text{\hspace{1em}(5.54)}$$

类似地，解调后的频率编码的回波信号的一般表达式可表示为：
$$S(t)={\int }_{\text{object}}\rho (\mathbf{r})e^{-i\gamma {\mathbf{G}}_{\text{fe}}\cdot \mathbf{r}(t-T_E)}d\mathbf{r}\text{\hspace{1em}(5.55)}$$

其中$T_E$是回波时间，当$t=T_E$时，回波达到最大值。

一个重要问题是：同时开启 $G_x$、$G_y$ 和 $G_z$ 是否能为每个空间点分配唯一频率？答案是否定的。设拉莫尔频率为常数：

$$\gamma {\mathbf{G}}_{\text{fe}}\cdot \mathbf{r}=c\text{\hspace{1em}(5.56)}$$

• 在二维情况下，公式(5.56)定义了一族等频率线，所有这些线都垂直于 ${\mathbf{G}}_{\text{fe}}$。
• 在三维情况下，公式(5.56)定义了一族等频率平面， ${\mathbf{G}}_{\text{fe}}$正是该平面的法线方向。

因此，对于固定的频率编码梯度矢量 ${\mathbf{G}}_{\text{fe}}$，空间信息仅沿梯度方向进行频率编码。

相位编码

理解频率编码的原理后，相位编码就很容易理解了。相位编码使激发的磁共振信号的振荡相位线性依赖于其空间位置。

为了说得更加明白一点，我们继续考虑一维情况，在射频脉冲后开启持续时间为$T_{\text{pe}}$的梯度$G_x$，然后关闭梯度，此时的信号为：
$$dS(x,t)=\{\begin{array}{ll}\rho (x)e^{-i\gamma (B_0+G_{x}x)t}& 0\le t\le T_{\text{pe}}\\ \rho (x)e^{-i\gamma G_{x}x{T}_{\text{pe}}}{e}^{-i\gamma B_{0}t}& T_{\text{pe}}\le t\end{array}\text{\hspace{1em}(5.57)}$$

在时间间隔 $T_{\text{pe}}$ 后，来自不同 $x$ 位置的信号积累了不同的相位角：
$$\varphi (x)=-\gamma G_{x}x{T}_{\text{pe}}\text{\hspace{1em}(5.58)}$$

由于 $\varphi (x)$ 与信号位置 $x$ 线性相关，我们称其为相位编码。 $G_x$被称为相位编码梯度，$T_{\text{pe}}$ 为相位编码间隔。

可以看到频率编码和相位编码的区别在于：频率编码一旦结束，不同位置的信号就会具备不同的相位角，这个相位角也是随空间位置不同而不同，就形成了相位编码，所以相位编码相当于给了不同位置的信号以不同的初态（初始相位角）。如下图所示：

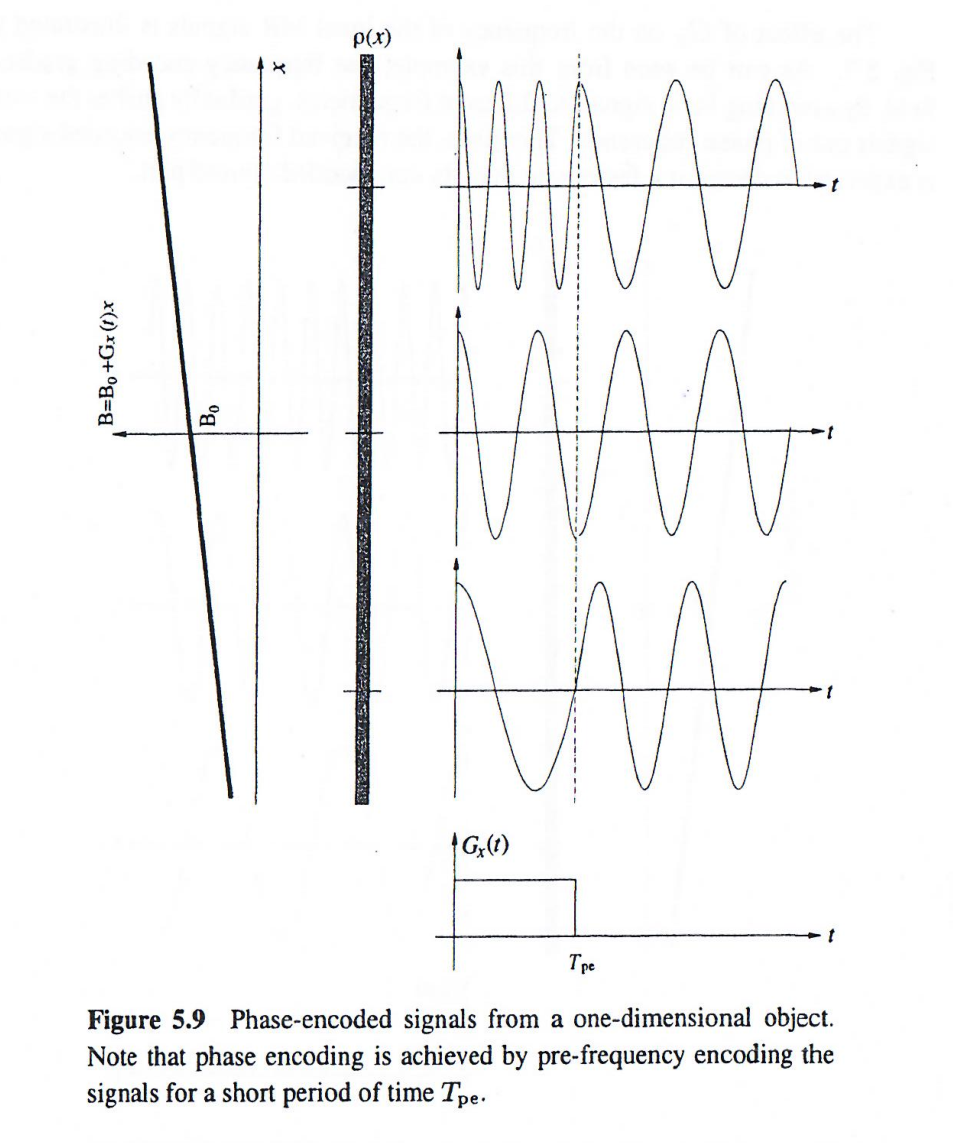
对于多维物体，通过同时在相位编码期间开启 $G_x$、$G_y$ 和 $G_z$ 可沿任意方向进行相位编码：
$${\mathbf{G}}_{\text{pe}}=(G_x,G_y,G_z),0\le t\le T_{\text{pe}}\text{\hspace{1em}(5.59)}$$

初始相位角为：
$$\varphi (\mathbf{r})=-\gamma {\mathbf{G}}_{\text{pe}}\cdot \mathbf{r}{T}_{\text{pe}}\text{\hspace{1em}(5.60)}$$

接收到的信号是所有局部相位编码信号之和：
$$S(t)={\int }_{\text{object}}dS(\mathbf{r},t)=\left[{\int }_{\text{object}}\rho (\mathbf{r})e^{-i\gamma {\mathbf{G}}_{\text{pe}}\cdot \mathbf{r}{T}_{\text{pe}}}d\mathbf{r}\right]e^{-i{\omega }_{0}t}\text{\hspace{1em}(5.61)}$$

解调（即去除载波信号 $e^{-i{\omega }_{0}t}$）后，得到
$$S(t)={\int }_{\text{object}}dS(\mathbf{r},t)={\int }_{\text{object}}\rho (\mathbf{r})e^{-i\gamma {\mathbf{G}}_{\text{pe}}\cdot \mathbf{r}{T}_{\text{pe}}}d\mathbf{r}$$