当前位置：首页 > news >正文

Leetcode+Java+图论+岛屿问题

news 2025/9/30 7:23:31

99.计数孤岛

题目描述
给定一个由 1（陆地）和 0（水）组成的矩阵，你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成，并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M，表示矩阵的行数和列数。
后续 N 行，每行包含 M 个数字，数字为 1 或者 0。
输出描述
输出一个整数，表示岛屿的数量。如果不存在岛屿，则输出 0。
输入示例
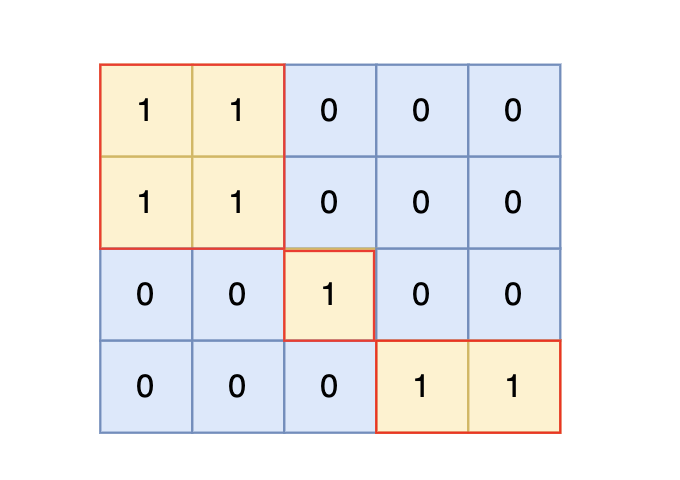
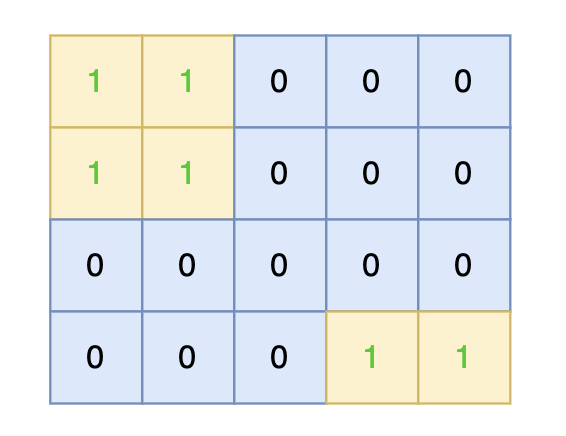
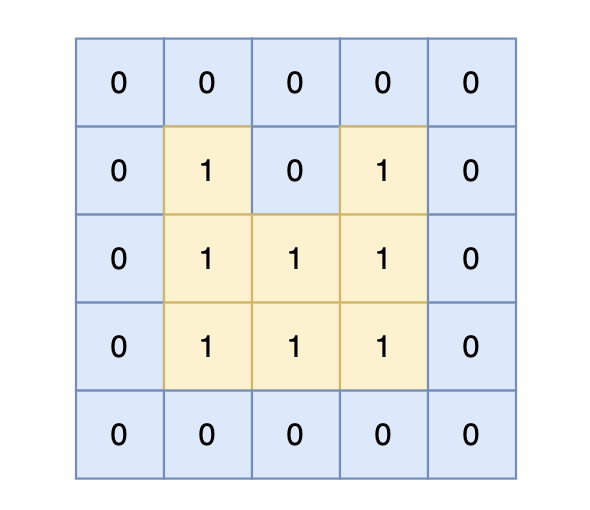
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
3
提示信息
根据测试案例中所展示，岛屿数量共有 3 个，所以输出 3。
数据范围：
1 <= N, M <= 50

原理

问题本质：
给定一个 N × M 的矩阵 graph，其中 1 表示陆地，0 表示水。
岛屿是由水平或垂直方向（上下左右）相连的 1 组成的区域。
需要计算矩阵中岛屿的数量。
每次找到一个未访问的陆地（graph[i][j] == 1），通过 BFS 或 DFS 将整个岛屿标记为已访问，并将岛屿计数加 1。
BFS 和 DFS 的核心思想：
BFS：使用队列，从起点开始逐层探索相邻的陆地（1），将所有相连的陆地标记为已访问，形成一个岛屿。
DFS：使用递归，从起点开始深度优先探索相邻的陆地，将所有相连的陆地标记为已访问，形成一个岛屿。
两种方法都通过 visited 数组避免重复访问，确保每个岛屿只计数一次。
为什么用 BFS/DFS？
BFS 和 DFS 适合处理图的连通性问题，能够高效遍历所有相连的陆地。
时间复杂度为 O(N × M)，因为每个格子最多访问一次；空间复杂度为 O(N × M)（visited 数组）或 O(min(N, M))（BFS 队列/DFS 递归栈）。
算法步骤：
初始化 visited 数组，标记所有格子为未访问。
遍历矩阵 graph：
如果遇到未访问的陆地（graph[i][j] == 1 && !visited[i][j]），岛屿计数加 1。
使用 BFS 或 DFS 遍历并标记整个岛屿（所有相连的 1）。
返回岛屿计数。

代码

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上static int result = 0; // 岛屿计数public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 初始化矩阵和访问标记数组int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];// 读取输入矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();// 遍历矩阵，寻找未访问的陆地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {result++; // 发现新岛屿，计数加 1bfs(graph, visited, n, m, i, j); // 使用 BFS 标记整个岛屿}}}System.out.print(result); // 输出岛屿数量}public static void bfs(int[][] graph, boolean[][] visited, int n, int m, int q, int p) {Queue<int[]> queue = new ArrayDeque<>();// 将起点加入队列并标记为已访问queue.add(new int[]{q, p});visited[q][p] = true; // 标记起点while (!queue.isEmpty()) {int[] temp = queue.poll();int curx = temp[0];int cury = temp[1];// 探索四个方向for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 检查边界和是否为未访问的陆地if (nextx < 0 || nexty < 0 || nextx >= n || nexty >= m) continue;if (!visited[nextx][nexty] && graph[nextx][nexty] == 1) {queue.add(new int[]{nextx, nexty});visited[nextx][nexty] = true; // 标记为已访问}}}}
}

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上static int result = 0; // 岛屿计数public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 初始化矩阵和访问标记数组int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];// 读取输入矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();// 遍历矩阵，寻找未访问的陆地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {result++; // 发现新岛屿，计数加 1dfs(i, j, visited, graph); // 使用 DFS 标记整个岛屿}}}System.out.print(result); // 输出岛屿数量}public static void dfs(int curx, int cury, boolean[][] visited, int[][] graph) {visited[curx][cury] = true; // 标记当前格子为已访问// 探索四个方向for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 检查边界和是否为未访问的陆地if (nextx < 0 || nexty < 0 || nextx >= graph.length || nexty >= graph[0].length) {continue;}if (graph[nextx][nexty] == 1 && !visited[nextx][nexty]) {dfs(nextx, nexty, visited, graph); // 递归探索}}}
}

100.最大岛屿的面积

题目描述
给定一个由 1（陆地）和 0（水）组成的矩阵，计算岛屿的最大面积。岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿由水平方向或垂直方向上相邻的陆地连接而成，并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M，表示矩阵的行数和列数。后续 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。
输出描述
输出一个整数，表示岛屿的最大面积。如果不存在岛屿，则输出 0。
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
4
提示信息
样例输入中，岛屿的最大面积为 4。
数据范围：
1 <= M, N <= 50。

原理

问题本质：
给定一个 N × M 的矩阵 graph，其中 1 表示陆地，0 表示水。
岛屿是由水平或垂直方向（上下左右）相连的 1 组成的区域。
需要计算所有岛屿中面积最大的那个，面积定义为岛屿中 1 的总数。
如果矩阵中没有岛屿（全是 0），返回 0。
BFS 和 DFS 的核心思想：
BFS：使用队列，从起点开始逐层探索相邻的陆地（1），统计连通区域的格子数（面积），并标记已访问。
DFS：使用递归，从起点开始深度优先探索相邻的陆地，统计连通区域的格子数，并标记已访问。
遍历矩阵，找到每个未访问的陆地格子，计算其岛屿面积，更新最大面积。
为什么用 BFS/DFS？
BFS 和 DFS 适合处理图的连通性问题，能够高效遍历所有相连的陆地格子，计算岛屿面积。
时间复杂度为 O(N × M)，因为每个格子最多访问一次；空间复杂度为 O(N × M)（visited 数组）或 O(min(N, M))（BFS 队列/DFS 递归栈）。
算法步骤：
初始化 visited 数组，标记所有格子为未访问。
初始化最大面积 max 为 0。
遍历矩阵 graph：
如果遇到未访问的陆地（graph[i][j] == 1 && !visited[i][j]），使用 BFS 或 DFS 计算该岛屿的面积。
更新最大面积 max。
返回最大面积 max。

代码

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 初始化矩阵和访问标记数组int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];// 读取输入矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();int maxArea = 0; // 最大岛屿面积// 遍历矩阵，寻找未访问的陆地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {int area = bfs(i, j, visited, graph); // 计算当前岛屿面积maxArea = Math.max(maxArea, area); // 更新最大面积}}}System.out.print(maxArea); // 输出最大面积}public static int bfs(int q, int p, boolean[][] visited, int[][] graph) {int area = 1; // 初始化当前岛屿面积Queue<int[]> queue = new ArrayDeque<>();queue.add(new int[]{q, p});visited[q][p] = true; // 标记起点while (!queue.isEmpty()) {int[] temp = queue.poll();int curx = temp[0];int cury = temp[1];// 探索四个方向for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 检查边界和是否为未访问的陆地if (nextx < 0 || nexty < 0 || nextx >= graph.length || nexty >= graph[0].length) {continue;}if (!visited[nextx][nexty] && graph[nextx][nexty] == 1) {area++; // 增加面积queue.add(new int[]{nextx, nexty});visited[nextx][nexty] = true; // 标记为已访问}}}return area; // 返回当前岛屿面积}
}

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();int[][] graph = new int[n][m];for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();int maxArea = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (graph[i][j] == 1) {int area = bfs(i, j, graph);maxArea = Math.max(maxArea, area);}}}System.out.print(maxArea);}public static int bfs(int q, int p, int[][] graph) {int area = 1;Queue<int[]> queue = new ArrayDeque<>();queue.add(new int[]{q, p});graph[q][p] = 0; // 标记为已访问while (!queue.isEmpty()) {int[] temp = queue.poll();int curx = temp[0];int cury = temp[1];for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];if (nextx < 0 || nexty < 0 || nextx >= graph.length || nexty >= graph[0].length) {continue;}if (graph[nextx][nexty] == 1) {area++;queue.add(new int[]{nextx, nexty});graph[nextx][nexty] = 0; // 标记为已访问}}}return area;}
}

101.孤岛的总面积

题目描述
给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域，且完全被陆地单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要计算所有孤岛的总面积，岛屿面积的计算方式为组成岛屿的陆地的总数。
输入描述
第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0。
输出描述
输出一个整数，表示所有孤岛的总面积，如果不存在孤岛，则输出 0。
输入示例
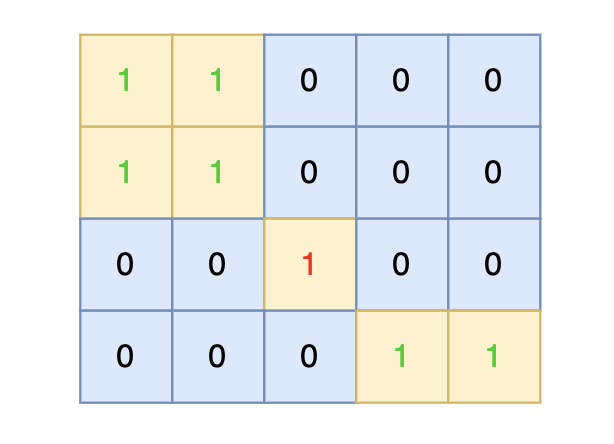
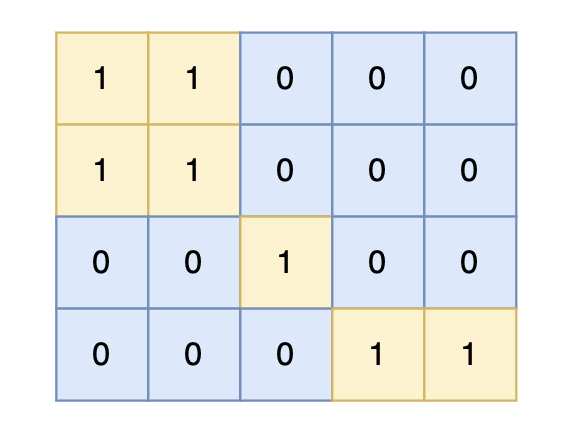
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
1
提示信息
在矩阵中心部分的岛屿，因为没有任何一个单元格接触到矩阵边缘，所以该岛屿属于孤岛，总面积为 1。
数据范围：
1 <= M, N <= 50。

原理

问题本质：
给定一个 N × M 的矩阵 graph，其中 1 表示陆地，0 表示水。
岛屿是由水平或垂直方向（上下左右）相连的 1 组成的区域。
孤岛是那些不接触矩阵边缘的岛屿，即岛屿中没有一个格子位于矩阵的边界（i == 0, i == N-1, j == 0, 或 j == M-1）。
需要计算所有孤岛的面积之和，面积为岛屿中 1 的总数。
如果没有孤岛，返回 0。
BFS 和 DFS 的核心思想：
BFS：使用队列，从起点开始逐层探索相连的陆地格子，统计面积，并检查是否接触边界。
DFS：使用递归，从起点开始深度优先探索相连的陆地格子，统计面积，并检查是否接触边界。
遍历矩阵，找到每个未访问的陆地格子，计算其岛屿面积，并判断是否为孤岛（不接触边界）。如果是孤岛，累加其面积。
为什么用 BFS/DFS？
BFS 和 DFS 适合处理图的连通性问题，能够高效遍历所有相连的陆地格子，计算岛屿面积并检查边界接触情况。
时间复杂度为 O(N × M)，每个格子最多访问一次；空间复杂度为 O(N × M)（visited 数组）或 O(min(N, M))（BFS 队列/DFS 递归栈）。
算法步骤：
初始化 visited 数组，标记所有格子为未访问。
初始化总面积 sum 为 0。
遍历矩阵 graph：
如果遇到未访问的陆地（graph[i][j] == 1 && !visited[i][j]），使用 BFS 或 DFS：
计算岛屿面积。
检查岛屿是否接触边界（若任一格子在边界上，则不是孤岛）。
如果是孤岛，累加面积到 sum。
返回总面积 sum。

代码

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 初始化矩阵和访问标记数组int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];// 读取输入矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();int totalArea = 0; // 所有孤岛的总面积// 遍历矩阵，寻找未访问的陆地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {int[] result = dfs(i, j, visited, graph, n, m); // 返回面积和是否为孤岛if (result[1] == 1) { // 如果是孤岛，累加面积totalArea += result[0];}}}}System.out.print(totalArea); // 输出总面积}public static int[] dfs(int curx, int cury, boolean[][] visited, int[][] graph, int n, int m) {visited[curx][cury] = true; // 标记当前格子为已访问int area = 1; // 初始化当前岛屿面积boolean isIsolated = (curx != 0 && curx != n - 1 && cury != 0 && cury != m - 1); // 检查是否在边界// 探索四个方向for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 如果接触边界，标记非孤岛if (nextx < 0 || nexty < 0 || nextx >= n || nexty >= m) {isIsolated = false;continue;}// 如果格子在边界上，标记非孤岛

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 初始化矩阵和访问标记数组int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];// 读取输入矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();int totalArea = 0; // 所有孤岛的总面积// 遍历矩阵，寻找未访问的陆地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {int[] result = bfs(i, j, visited, graph, n, m); // 返回面积和是否为孤岛if (result[1] == 1) { // 如果是孤岛，累加面积totalArea += result[0];}}}}System.out.print(totalArea); // 输出总面积}public static int[] bfs(int q, int p, boolean[][] visited, int[][] graph, int n, int m) {int area = 1; // 当前岛屿面积boolean isIsolated = (q != 0 && q != n - 1 && p != 0 && p != m - 1); // 检查起点是否在边界Queue<int[]> queue = new ArrayDeque<>();queue.add(new int[]{q, p});visited[q][p] = true;while (!queue.isEmpty()) {int[] temp = queue.poll();int curx = temp[0];int cury = temp[1];// 探索四个方向for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 如果接触边界，标记非孤岛if (nextx < 0 || nexty < 0 || nextx >= n || nexty >= m) {isIsolated = false;continue;}// 如果格子在边界上，标记非孤岛if (nextx == 0 || nextx == n - 1 || nexty == 0 || nexty == m - 1) {isIsolated = false;}// 如果是未访问的陆地，继续探索if (!visited[nextx][nexty] && graph[nextx][nexty] == 1) {area++;queue.add(new int[]{nextx, nexty});visited[nextx][nexty] = true;}}}return new int[]{area, isIsolated ? 1 : 0}; // 返回面积和是否为孤岛}
}

102.沉没孤岛

题目描述
给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域，且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要将所有孤岛“沉没”，即将孤岛中的所有陆地单元格（1）转变为水域单元格（0）。
输入描述
第一行包含两个整数 N, M，表示矩阵的行数和列数。
之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。
输出描述
输出将孤岛“沉没”之后的岛屿矩阵。注意：每个元素后面都有一个空格
输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
1 1 0 0 0
1 1 0 0 0
0 0 0 0 0
0 0 0 1 1
提示信息
将孤岛沉没。
数据范围：
1 <= M, N <= 50。

原理

问题本质：
给定一个 N × M 的矩阵 graph，其中 1 表示陆地，0 表示水。
岛屿是由水平或垂直方向（上下左右）相连的 1 组成的区域。
孤岛是那些不接触矩阵边缘的岛屿，即岛屿中没有一个格子位于边界（i == 0, i == N-1, j == 0, 或 j == M-1）。
需要将所有孤岛的陆地格子（1）改为水域格子（0），并输出修改后的矩阵。
输出格式要求每个元素后加空格，每行末尾换行。
BFS 和 DFS 的核心思想：
BFS：使用队列，从起点开始逐层探索相连的陆地格子，检查是否为孤岛（不接触边界），如果是孤岛，则将所有格子改为 0。
DFS：使用递归，从起点开始深度优先探索相连的陆地格子，检查是否为孤岛，如果是孤岛，则将所有格子改为 0。
遍历矩阵，找到每个未访问的陆地格子，判断其是否为孤岛，如果是孤岛，则修改矩阵。
为什么用 BFS/DFS？
BFS 和 DFS 适合处理图的连通性问题，能够高效遍历所有相连的陆地格子，判断是否为孤岛并修改格子。
时间复杂度为 O(N × M)，每个格子最多访问一次；空间复杂度为 O(N × M)（visited 数组）或 O(min(N, M))（BFS 队列/DFS 递归栈）。
算法步骤：
初始化 visited 数组，标记所有格子为未访问。
遍历矩阵 graph：
如果遇到未访问的陆地（graph[i][j] == 1 && !visited[i][j]），使用 BFS 或 DFS：
检查岛屿是否接触边界（若任一格子在边界上，则不是孤岛）。
如果是孤岛，将岛屿中的所有 1 改为 0。
输出修改后的矩阵。

代码

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 初始化矩阵和访问标记数组int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];// 读取输入矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();// 遍历矩阵，寻找未访问的陆地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {bfs(i, j, visited, graph, n, m); // 处理岛屿}}}// 输出修改后的矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {System.out.print(graph[i][j] + " ");}System.out.print("\n");}}public static void bfs(int q, int p, boolean[][] visited, int[][] graph, int n, int m) {boolean isIsolated = (q != 0 && q != n - 1 && p != 0 && p != m - 1); // 检查起点是否在边界List<int[]> islandCells = new ArrayList<>(); // 存储岛屿格子islandCells.add(new int[]{q, p}); // 添加起点visited[q][p] = true;Queue<int[]> queue = new ArrayDeque<>();queue.add(new int[]{q, p});while (!queue.isEmpty()) {int[] temp = queue.poll();int curx = temp[0];int cury = temp[1];// 探索四个方向for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 如果接触边界，标记非孤岛if (nextx < 0 || nexty < 0 || nextx >= n || nexty >= m) {isIsolated = false;continue;}// 如果格子在边界上，标记非孤岛if (nextx == 0 || nextx == n - 1 || nexty == 0 || nexty == m - 1) {isIsolated = false;}// 如果是未访问的陆地，继续探索if (!visited[nextx][nexty] && graph[nextx][nexty] == 1) {queue.add(new int[]{nextx, nexty});islandCells.add(new int[]{nextx, nexty}); // 记录格子visited[nextx][nexty] = true;}}}// 如果是孤岛，将所有格子改为 0if (isIsolated) {for (int[] cell : islandCells) {graph[cell[0]][cell[1]] = 0;}}}
}

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 初始化矩阵和访问标记数组int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];// 读取输入矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();// 遍历矩阵，寻找未访问的陆地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {dfs(i, j, visited, graph, n, m); // 处理岛屿}}}// 输出修改后的矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {System.out.print(graph[i][j] + " ");}System.out.print("\n");}}public static void dfs(int curx, int cury, boolean[][] visited, int[][] graph, int n, int m) {visited[curx][cury] = true;boolean isIsolated = (curx != 0 && curx != n - 1 && cury != 0 && cury != m - 1);List<int[]> islandCells = new ArrayList<>();islandCells.add(new int[]{curx, cury});// 探索四个方向for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 如果接触边界，标记非孤岛if (nextx < 0 || nexty < 0 || nextx >= n || nexty >= m) {isIsolated = false;continue;}// 如果格子在边界上，标记非孤岛if (nextx == 0 || nextx == n - 1 || nexty == 0 || nexty == m - 1) {isIsolated = false;}// 如果是未访问的陆地，继续递归if (!visited[nextx][nexty] && graph[nextx][nexty] == 1) {dfs(nextx, nexty, visited, graph, n, m);islandCells.add(new int[]{nextx, nexty});}}// 如果是孤岛，将所有格子改为 0if (isIsolated) {for (int[] cell : islandCells) {graph[cell[0]][cell[1]] = 0;}}}
}

103.高山流水

题目描述
现有一个 N × M 的矩阵，每个单元格包含一个数值，这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界，而矩阵的右边界和下边界被视为第二组边界。
矩阵模拟了一个地形，当雨水落在上面时，水会根据地形的倾斜向低处流动，但只能从较高或等高的地点流向较低或等高并且相邻（上下左右方向）的地点。我们的目标是确定那些单元格，从这些单元格出发的水可以达到第一组边界和第二组边界。
输入描述
第一行包含两个整数 N 和 M，分别表示矩阵的行数和列数。
后续 N 行，每行包含 M 个整数，表示矩阵中的每个单元格的高度。
输出描述
输出共有多行，每行输出两个整数，用一个空格隔开，表示可达第一组边界和第二组边界的单元格的坐标，输出顺序任意。
输入示例
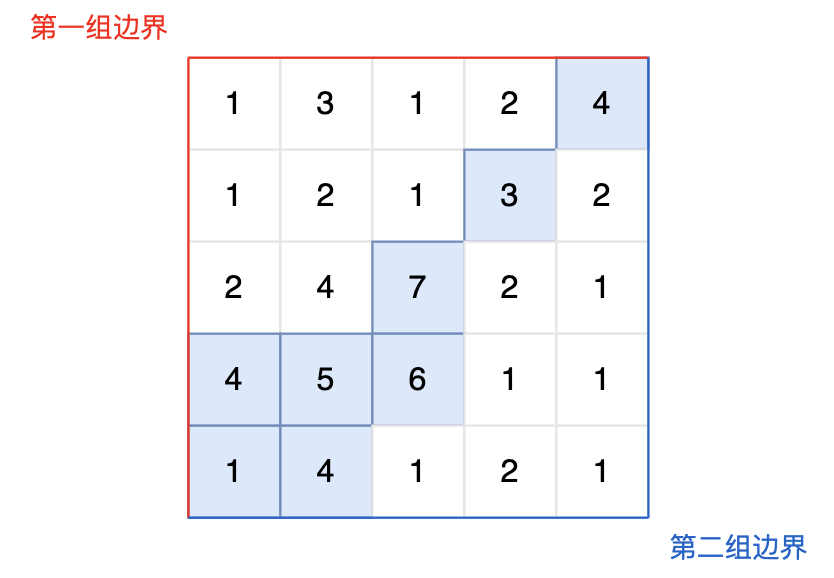
5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1
输出示例
0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1
提示信息
图中的蓝色方块上的雨水既能流向第一组边界，也能流向第二组边界。所以最终答案为所有蓝色方块的坐标。
数据范围：
1 <= M, N <= 100。

原理

问题本质：
给定一个 N × M 的矩阵 graph，每个格子包含一个整数表示高度。
雨水从一个格子出发，沿上下左右方向流动，只能流向高度小于或等于当前格子的相邻格子。
第一组边界：矩阵的左边界（j == 0）和上边界（i == 0）。
第二组边界：矩阵的右边界（j == M-1）和下边界（i == N-1）。
目标是找到所有既能流向第一组边界又能流向第二组边界的格子坐标。
BFS 和 DFS 的核心思想：
BFS：从第一组边界和第二组边界的格子分别开始，使用队列进行广度优先搜索，标记所有可以从这些边界逆向到达的格子（即雨水可以流向该边界的格子）。最终检查哪些格子同时被两组边界标记。
DFS：类似地，从边界格子开始，使用递归进行深度优先搜索，标记可达格子。
使用两个布尔数组 firEdge 和 secEdge 分别记录从第一组边界和第二组边界可达的格子。
最后输出同时出现在 firEdge 和 secEdge 中的格子坐标。
为什么用 BFS/DFS？
BFS 和 DFS 适合处理图的连通性问题，能够高效探索从边界出发的可达格子。
由于雨水流动是基于高度的单向约束（从高到低或等高），需要从边界逆向搜索（从低到高或等高），以找到所有可能的起点。
时间复杂度为 O(N × M)，每个格子最多访问一次；空间复杂度为 O(N × M)（标记数组）或 O(min(N, M))（BFS 队列/DFS 递归栈）。
算法步骤：
初始化两个布尔数组 firEdge 和 secEdge，标记从第一组边界和第二组边界可达的格子。
对第一组边界（左边界 j == 0 和上边界 i == 0）运行 BFS/DFS，标记可达格子。
对第二组边界（右边界 j == M-1 和下边界 i == N-1）运行 BFS/DFS，标记可达格子。
遍历矩阵，输出同时在 firEdge 和 secEdge 中标记为 true 的格子坐标。

代码

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 初始化矩阵int[][] graph = new int[n][m];boolean[][] firEdge = new boolean[n][m];boolean[][] secEdge = new boolean[n][m];// 读取输入矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();// 从第一组边界（左边界和上边界）进行 BFSfor (int i = 0; i < n; i++) {bfs(i, 0, firEdge, graph, n, m); // 左边界}for (int j = 0; j < m; j++) {bfs(0, j, firEdge, graph, n, m); // 上边界}// 从第二组边界（右边界和下边界）进行 BFSfor (int i = 0; i < n; i++) {bfs(i, m - 1, secEdge, graph, n, m); // 右边界}for (int j = 0; j < m; j++) {bfs(n - 1, j, secEdge, graph, n, m); // 下边界}// 输出同时可达第一组和第二组边界的格子坐标for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (firEdge[i][j] && secEdge[i][j]) {System.out.println(i + " " + j);}}}}public static void bfs(int curx, int cury, boolean[][] visited, int[][] graph, int n, int m) {Queue<int[]> queue = new ArrayDeque<>();queue.add(new int[]{curx, cury});visited[curx][cury] = true;while (!queue.isEmpty()) {int[] temp = queue.poll();curx = temp[0];cury = temp[1];// 探索四个方向for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 检查边界和已访问状态if (nextx < 0 || nexty < 0 || nextx >= n || nexty >= m || visited[nextx][nexty]) {continue;}// 雨水从高到低或等高流动，逆向搜索需从低到高或等高if (graph[nextx][nexty] >= graph[curx][cury]) {visited[nextx][nexty] = true;queue.add(new int[]{nextx, nexty});}}}}
}

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 初始化矩阵和访问标记数组int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];// 读取输入矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();// 遍历矩阵，寻找未访问的陆地for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {dfs(i, j, visited, graph, n, m); // 处理岛屿}}}// 输出修改后的矩阵for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {System.out.print(graph[i][j] + " ");}System.out.print("\n");}}public static void dfs(int curx, int cury, boolean[][] visited, int[][] graph, int n, int m) {visited[curx][cury] = true;boolean isIsolated = (curx != 0 && curx != n - 1 && cury != 0 && cury != m - 1);List<int[]> islandCells = new ArrayList<>();islandCells.add(new int[]{curx, cury});// 探索四个方向for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];// 如果接触边界，标记非孤岛if (nextx < 0 || nexty < 0 || nextx >= n || nexty >= m) {isIsolated = false;continue;}// 如果格子在边界上，标记非孤岛if (nextx == 0 || nextx == n - 1 || nexty == 0 || nexty == m - 1) {isIsolated = false;}// 如果是未访问的陆地，继续递归if (!visited[nextx][nexty] && graph[nextx][nexty] == 1) {dfs(nextx, nexty, visited, graph, n, m);islandCells.add(new int[]{nextx, nexty});}}// 如果是孤岛，将所有格子改为 0if (isIsolated) {for (int[] cell : islandCells) {graph[cell[0]][cell[1]] = 0;}}}
}

104.建造最大岛屿

题目描述
给定一个由 1（陆地）和 0（水）组成的矩阵，你最多可以将矩阵中的一格水变为一块陆地，在执行了此操作之后，矩阵中最大的岛屿面积是多少。
岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。
输出描述
输出一个整数，表示最大的岛屿面积。
输入示例
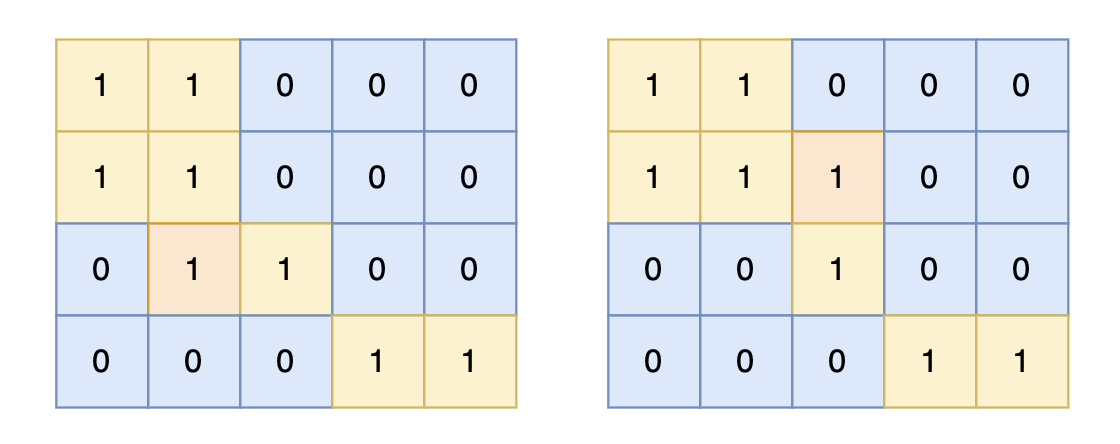
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1
输出示例
6
提示信息
对于上面的案例，有两个位置可将 0 变成 1，使得岛屿的面积最大，即 6。
数据范围：
1 <= M, N <= 50。

原理

问题本质：
给定一个 N × M 的矩阵 graph，其中 1 表示陆地，0 表示水。
岛屿是由水平或垂直方向（上下左右）相连的 1 组成的区域。
你可以选择一格水（0）变为陆地（1），可能合并多个岛屿或扩展现有岛屿。
目标是计算操作后可能的最大岛屿面积（即最大连通陆地格子数）。
输出一个整数，表示最大岛屿面积。
核心思路：
步骤 1：使用 DFS 或 BFS 遍历矩阵，识别所有现有岛屿，计算每个岛屿的面积，并为每个岛屿分配一个唯一标识（索引）。将岛屿索引和面积存储在 HashMap 中。
步骤 2：遍历每个水格子（0），检查其四个相邻格子（上下左右）。如果相邻格子属于不同岛屿，将水格子变为陆地可以合并这些岛屿，面积为 1（新陆地）加上相邻岛屿的面积之和。
步骤 3：使用 HashSet 去重，确保相邻的多个格子属于同一岛屿时只计算一次面积。
步骤 4：比较原始岛屿的最大面积和改变水格子后的最大面积，返回较大值。
为什么使用 DFS/BFS 和 HashSet？
DFS 和 BFS 适合处理网格中的连通性问题，能高效计算岛屿面积并标记岛屿。
HashSet 用于在检查水格子时去重相邻岛屿的索引，避免重复计算同一岛屿的面积。
时间复杂度：O(N × M)（遍历网格找岛屿）+ O(N × M)（检查水格子），总计 O(N × M)。
空间复杂度：O(N × M)（visited 数组或 islandMap）+ O(min(N, M))（DFS 递归栈或 BFS 队列）+ O(K)（HashMap 和 HashSet，K 为岛屿数量）。
算法步骤：
初始化 visited 数组或 islandMap 记录岛屿索引。
遍历矩阵，找到所有岛屿：
对每个未访问的陆地格子（graph[i][j] == 1），使用 DFS/BFS 计算面积，分配唯一索引，存储到 HashMap。
遍历矩阵，检查每个水格子（graph[i][j] == 0）：
检查四个相邻格子的岛屿索引，使用 HashSet 收集唯一索引。
计算潜在面积：1（新陆地）+ 相邻岛屿面积之和。
跟踪最大面积，考虑原始岛屿和改变水格子后的情况。
输出最大面积。

代码

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];int[][] islandMap = new int[n][m]; // 存储每个格子的岛屿索引Map<Integer, Integer> islandAreas = new HashMap<>(); // 存储岛屿索引到面积的映射for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();int islandIndex = 1; // 岛屿索引从 1 开始int maxArea = 0; // 原始岛屿的最大面积// 步骤 1：找到所有岛屿及其面积for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {int area = bfs(i, j, visited, graph, islandMap, islandIndex);islandAreas.put(islandIndex, area);maxArea = Math.max(maxArea, area);islandIndex++;}}}// 步骤 2：检查每个水格子for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (graph[i][j] == 0) {int sum = 1; // 新陆地的面积Set<Integer> adjacentIslands = new HashSet<>();// 检查四个相邻格子for (int k = 0; k < 4; k++) {int nextx = i + dir[k][0];int nexty = j + dir[k][1];if (nextx < 0 || nexty < 0 || nextx >= n || nexty >= m) continue;if (islandMap[nextx][nexty] > 0) { // 如果相邻格子属于某个岛屿adjacentIslands.add(islandMap[nextx][nexty]);}}// 累加唯一相邻岛屿的面积for (int idx : adjacentIslands) {sum += islandAreas.get(idx);}maxArea = Math.max(maxArea, sum);}}}System.out.print(maxArea);}public static int bfs(int curx, int cury, boolean[][] visited, int[][] graph, int[][] islandMap, int index) {int area = 1;Queue<int[]> queue = new ArrayDeque<>();queue.add(new int[]{curx, cury});visited[curx][cury] = true;islandMap[curx][cury] = index;while (!queue.isEmpty()) {int[] temp = queue.poll();curx = temp[0];cury = temp[1];for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];if (nextx < 0 || nexty < 0 || nextx >= graph.length || nexty >= graph[0].length) continue;if (!visited[nextx][nexty] && graph[nextx][nexty] == 1) {area++;visited[nextx][nexty] = true;islandMap[nextx][nexty] = index;queue.add(new int[]{nextx, nexty});}}}return area;}
}

import java.util.*;public class Main {static int[][] dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; // 四个方向：右、左、下、上public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();int[][] graph = new int[n][m];boolean[][] visited = new boolean[n][m];int[][] islandMap = new int[n][m]; // 存储每个格子的岛屿索引Map<Integer, Integer> islandAreas = new HashMap<>(); // 存储岛屿索引到面积的映射for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {graph[i][j] = scanner.nextInt();}}scanner.close();int islandIndex = 1; // 岛屿索引从 1 开始int maxArea = 0; // 原始岛屿的最大面积// 步骤 1：找到所有岛屿及其面积for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (!visited[i][j] && graph[i][j] == 1) {int area = dfs(i, j, visited, graph, islandMap, islandIndex);islandAreas.put(islandIndex, area);maxArea = Math.max(maxArea, area);islandIndex++;}}}// 步骤 2：检查每个水格子for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (graph[i][j] == 0) {int sum = 1; // 新陆地的面积Set<Integer> adjacentIslands = new HashSet<>();// 检查四个相邻格子for (int k = 0; k < 4; k++) {int nextx = i + dir[k][0];int nexty = j + dir[k][1];if (nextx < 0 || nexty < 0 || nextx >= n || nexty >= m) continue;if (islandMap[nextx][nexty] > 0) { // 如果相邻格子属于某个岛屿adjacentIslands.add(islandMap[nextx][nexty]);}}// 累加唯一相邻岛屿的面积for (int idx : adjacentIslands) {sum += islandAreas.get(idx);}maxArea = Math.max(maxArea, sum);}}}System.out.print(maxArea);}public static int dfs(int curx, int cury, boolean[][] visited, int[][] graph, int[][] islandMap, int index) {visited[curx][cury] = true;islandMap[curx][cury] = index;int area = 1;for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];if (nextx < 0 || nexty < 0 || nextx >= graph.length || nexty >= graph[0].length) continue;if (!visited[nextx][nexty] && graph[nextx][nexty] == 1) {area += dfs(nextx, nexty, visited, graph, islandMap, index);}}return area;}
}

106.海岸线计算

题目描述
给定一个由 1（陆地）和 0（水）组成的矩阵，岛屿是被水包围，并且通过水平方向或垂直方向上相邻的陆地连接而成的。
你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿，假设组成岛屿的陆地边长都为 1，请计算海岸线，即：岛屿的周长。岛屿内部没有水域。
输入描述
第一行包含两个整数 N, M，表示矩阵的行数和列数。之后 N 行，每行包含 M 个数字，数字为 1 或者 0，表示岛屿的单元格。
输出描述
输出一个整数，表示岛屿的周长。
输入示例
5 5
0 0 0 0 0 
0 1 0 1 0
0 1 1 1 0
0 1 1 1 0
0 0 0 0 0
输出示例
14
提示信息
岛屿的周长为 14。
数据范围：
1 <= M, N <= 50。

原理

问题本质：
给定一个 N × M 的矩阵 graph，其中 1 表示陆地，0 表示水。
矩阵中恰好有一个岛屿，由水平或垂直方向（上下左右）相连的 1 组成，内部无水域。
岛屿的周长是所有陆地格子与水格子或矩阵边界相邻的边的总数（每个陆地格子边长为 1）。
需要计算岛屿的周长，并输出一个整数。
假设矩阵外均为水，边界检查需考虑矩阵外。
核心思路：
方法 1（简单遍历）：遍历矩阵中的每个陆地格子（graph[i][j] == 1），检查其四个方向（上、下、左、右）是否为水（0）或超出矩阵边界。每发现一个水格子或边界，贡献 1 单位周长。
方法 2（BFS/DFS）：从任意水格子开始，探索所有相连的水域，统计与陆地格子相邻的边数作为周长。
题目保证只有一个岛屿，内部无水域，因此只需找到岛屿并计算其边界。
为什么使用 BFS/DFS？
BFS 和 DFS 适合处理网格的连通性问题，可以从水格子出发找到所有与岛屿接壤的边界。
然而，对于周长计算，直接遍历陆地格子更简单高效，因为只需检查每个陆地格子的四条边。
时间复杂度：O(N × M)（遍历网格），空间复杂度：O(N × M)（visited 数组）或 O(min(N, M))（BFS 队列/DFS 栈）。
算法步骤：
简单方法：
遍历矩阵，找到每个陆地格子（graph[i][j] == 1）。
检查四个方向（上、下、左、右），如果相邻格子是水（0）或超出边界，增加周长计数。
BFS/DFS 方法：
从矩阵边界的水格子（0）开始 BFS/DFS，探索所有相连的水域。
每次遇到陆地格子（1），增加周长计数。
使用 visited 数组避免重复访问水格子。
输出总周长。

代码

import java.util.*;public class Main {static int[][] dir={{0,1},{0,-1},{1,0},{-1,0}};static int sum=0;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 节点编号从1到n，所以申请 n+1 这么大的数组int[][] graph = new int[n+2][m+2];boolean[][] visited =new boolean[n+2][m+2];for (int i = 1; i <= n; i++) {for(int j=1;j<=m;j++){graph[i][j] = scanner.nextInt();}}scanner.close();for(int i=0;i<n+2;i++){for(int j=0;j<m+2;j++){if(!visited[i][j] && graph[i][j]==0){dfs(visited,graph,i,j);}}}System.out.print(sum);}public static void dfs(boolean[][] visited,int[][] graph,int curx,int cury){for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];if (nextx < 0 || nexty < 0 || nextx >= graph.length || nexty >= graph[0].length) continue;if(graph[nextx][nexty]==1) sum++;if (!visited[nextx][nexty] && graph[nextx][nexty] == 0) {visited[nextx][nexty]=true;dfs(visited,graph,nextx,nexty);}}}
}

import java.util.*;public class Main {static int[][] dir={{0,1},{0,-1},{1,0},{-1,0}};static int sum=0;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();// 节点编号从1到n，所以申请 n+1 这么大的数组int[][] graph = new int[n+2][m+2];boolean[][] visited =new boolean[n+2][m+2];for (int i = 1; i <= n; i++) {for(int j=1;j<=m;j++){graph[i][j] = scanner.nextInt();}}scanner.close();for(int i=0;i<n+2;i++){for(int j=0;j<m+2;j++){if(!visited[i][j] && graph[i][j]==0){bfs(visited,graph,i,j);}}}System.out.print(sum);}public static void bfs(boolean[][] visited,int[][] graph,int curx,int cury){visited[curx][cury]=true;Queue<int[]> queue=new ArrayDeque<>();queue.add(new int[]{curx,cury});while(!queue.isEmpty()) {int[] temp= queue.poll();curx=temp[0];cury=temp[1];for (int i = 0; i < 4; i++) {int nextx = curx + dir[i][0];int nexty = cury + dir[i][1];if (nextx < 0 || nexty < 0 || nextx >= graph.length || nexty >= graph[0].length) continue;if(graph[nextx][nexty]==1) sum++;if (!visited[nextx][nexty] && graph[nextx][nexty] == 0) {visited[nextx][nexty]=true;queue.add(new int[]{nextx,nexty});}}}}
}

查看全文

http://www.dtcms.com/a/422612.html