C++程序设计上机作业(1)
目录
- 每日一句
- 实验目的
- 实验环境
- 1、水仙花数(Narcissistic number)
- 基本思路
- 思路实现设计
- 代码
- 代码解析
- 1.函数定义与参数说明:
- 2.参数合法性检查:
- 3.数字分解与幂计算:
- 4.主函数实现:
- 运行截图
- 结果分析
- 2、辗转相除法
- 基本思路
- 思路实现设计
- 代码
- 代码解析
- 1.循环结构实现(GreatestCommonDivisor 函数):
- 2.递归结构实现(gcd 函数):
- 3.测试函数(testGCD):
- 4.主函数(main):
- 运行截图
- 结果分析
- 3、最小公倍数
- 基本思路
- 思路实现设计
- 代码
- 代码解析
- 1.最大公约数函数(GreatestCommonDivisor):
- 2.两个数的最小公倍数函数(lcm):
- 3.三个数的最小公倍数函数(重载 lcm):
- 4.四个数的最小公倍数函数(重载 lcm):
- 5.测试函数:
- 6.主函数(main):
- 运行截图
- 结果分析
- 总结
每日一句
日出未必意味着光明
太阳也无非是一颗晨星而已
只有在我们醒着的时候
才是真正的破晓
—— 梭罗

实验目的
本实验旨在通过实际编程练习,深入理解和掌握 C++ 函数的相关知识与应用技巧,具体包括:
(1)函数的基本知识理解和运用,掌握函数的定义、声明、调用及参数传递方式
(2)函数默认参数值的使用方法,理解默认参数在函数重载和函数调用中的作用
(3)递归函数的设计与实现,掌握递归算法的基本思想和递归函数的执行过程
(4)函数重载的概念与应用,学会通过函数重载实现多态性,提高代码的灵活性和可读性
通过完成本次实验,培养分析问题、设计算法和编写程序的能力,为后续更复杂的程序设计打下坚实基础。
实验环境
操作系统:Windows 10专业版 X64
开发工具:VS code
编程语言:C++
编译标准:C++11
1、水仙花数(Narcissistic number)
水仙花数也被称为超完全数字不变数、自幂数等,水仙花数是指一个 3 位数,它的每个数位上的数字的 3次幂之和等于它本身。例如:1^3 + 5^3+ 3^3 = 153。
四叶玫瑰数是指一个 4 位数,它的每个数位上的数字的 4次幂之和等于它本身。
使用C++编程实现判断一个数是否是水仙花数或者四叶玫瑰数,函数原型如下:
// number : 带判断整数
// n : 数字位数,3-水仙花数,4-四叶玫瑰数
// 返回值: true-是,false-否
bool IsNarcis(int number, int n=3);
基本思路
要判断一个数是否为自幂数(水仙花数或四叶玫瑰数),需要完成以下步骤:
验证输入参数的合法性:n 只能是 3 或 4,对应 3 位数和 4 位数的自幂数
验证数字的位数是否与 n 一致:3 位数的范围是 100-999,4 位数的范围是 1000-9999
分解数字的每一位,计算每一位的 n 次幂之和
判断幂之和是否等于原数字,如果等于则是自幂数,否则不是
思路实现设计
1.参数合法性检查:首先检查 n 是否为 3 或 4,如果不是则返回 false
2.数字范围检查:根据 n 的值确定数字的合法范围(3 位数 100-999,4 位数 1000-9999),如果数字不在相应范围内则返回 false
3.数字分解与幂计算:
- 使用循环结构,通过取余运算(number % 10)提取数字的最后一位
- 计算该位的 n 次幂并累加到总和中
- 通过除法运算(number / 10)移除数字的最后一位
重复上述步骤直到数字变为 0
4.结果判断:比较累加的幂之和与原数字,如果相等则返回 true,否则返回 false
代码
#include <iostream>
using namespace std;// 判断数
bool IsNarcis(int number, int n = 3)
{// 检查n是否合法(仅支持3或4)if (n != 3 && n != 4){return false;}// 确定位数范围int min_val = (n == 3) ? 100 : 1000; // 3位数最小100,4位数最小1000int max_val = (n == 3) ? 999 : 9999; // 3位数最大999,4位数最大9999// 检查数字是否在合法范围内if (number < min_val || number > max_val){return false;}int temp = number;int sum = 0;// 计算每个数位的n次幂之和while (temp > 0){int digit = temp % 10; // 提取最后一位数字if (n == 3){sum += digit * digit * digit;}else{sum += digit * digit * digit * digit; // 4次方}temp /= 10; // 移除最后一位数字}// 判断总和是否等于原数字return (sum == number);
}int main()
{int num;cout << "请输入一个3位或4位整数:";cin >> num;// 检查输入的数字是否为3位或4位if ((num >= 100 && num <= 999) || (num >= 1000 && num <= 9999)){// 判断并输出结果bool isNarcissus = IsNarcis(num, 3);bool isRose = IsNarcis(num, 4);cout << num << " 是水仙花数(3位)吗?" << (isNarcissus ? " 是" : " 否") << endl;cout << num << " 是四叶玫瑰数(4位)吗?" << (isRose ? " 是" : " 否") << endl;}// 不符合要求的数else{cout << "数字不符合要求" << endl;}return 0;
}
代码解析
1.函数定义与参数说明:
- 函数IsNarcis接收两个参数,number是待判断的整数,n是数字的位数,默认值为 3
- 返回值为布尔类型,表示number是否为n位的自幂数
2.参数合法性检查:
- 首先检查n是否为 3 或 4,如果不是则返回 false,因为函数只支持这两种情况
- 根据n的值确定数字的合法范围,3 位数为100-999,4 位数为 1000-9999
- 如果number不在相应的范围内,则返回 false
3.数字分解与幂计算:
- 使用临时变量temp存储number的值,避免修改原变量
- 通过temp % 10提取最后一位数字
- 根据n的值计算该数字的 3 次方或 4次方,并累加到sum中
- 通过temp /= 10移除最后一位数字,继续处理下一位
- 循环直到temp变为 0,此时已处理完所有位数
4.主函数实现:
- 接收用户输入的数字,并检查其是否为 3 位或 4 位
- 调用IsNarcis函数分别判断该数字是否为水仙花数(n=3)和四叶玫瑰数(n=4)
- 输出判断结果
- 增加了额外的测试案例,自动测试已知的水仙花数和四叶玫瑰数
运行截图
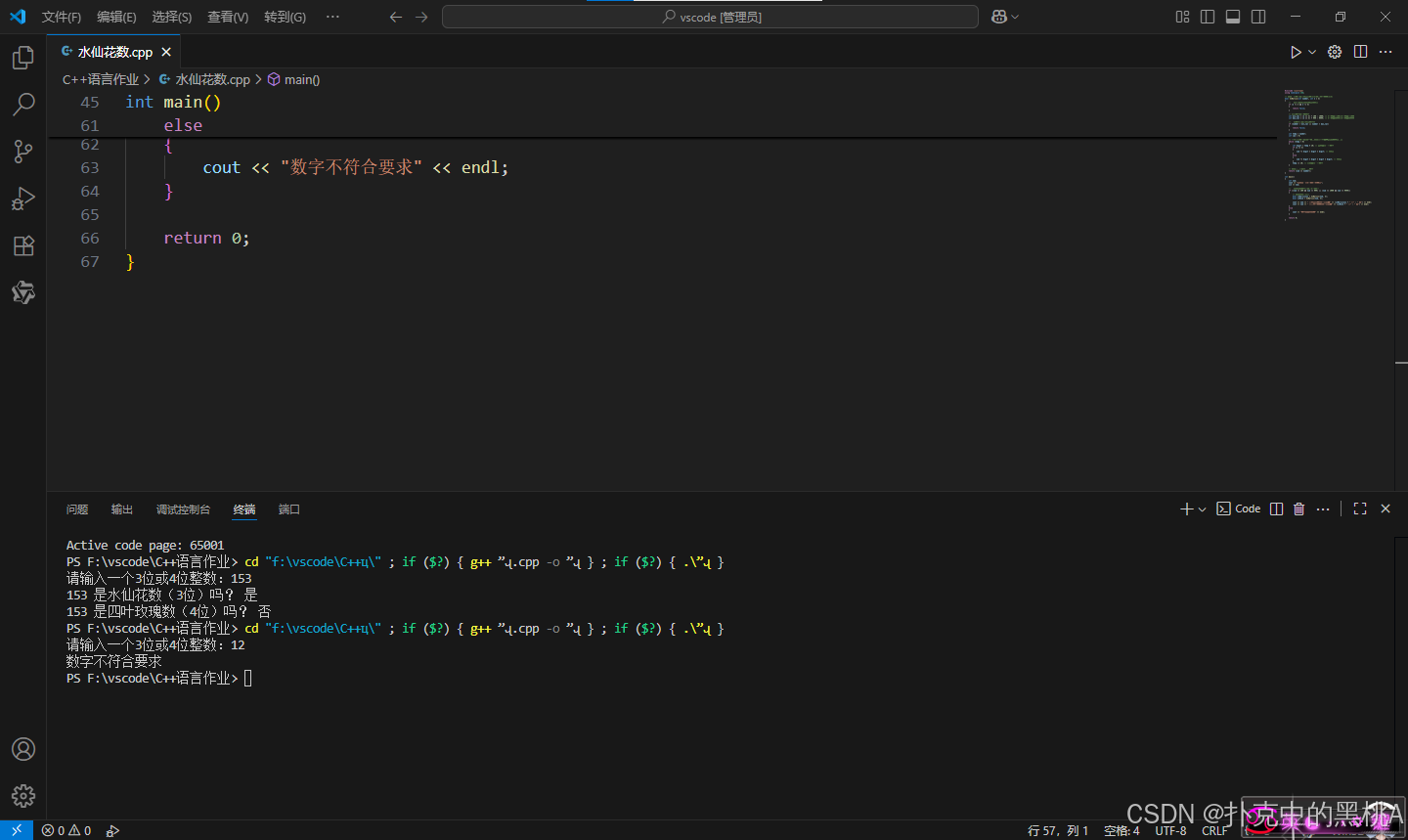
结果分析
程序与预定结果一样,可以接收 3 位或 4 位整数,判断是否为水仙花数(各位立方和等于自身)或四叶玫瑰数(各位四次方和等于自身),位数不合则提示 “数字不合要求”。
2、辗转相除法
辗转相除法,又称欧几里得算法,是一种用于计算两个正整数最大公约数(GCD)的经典算法,其核心原理基于数学公式 gcd(a, b) = gcd(b, a mod b),通过反复用除数除以余数直至余数为零,最终得到最大公约数。
使用C++编程实现上述方法,要求:
1)按照如下函数原型,使用循环结构实现函数。
int GreatestCommonDivisor(int a, int b);
2)使用递归方式实现函数。
int gcd(int a, int b);
3)使用4组以上测试数据测试上述代码的正确性。
基本思路
最大公约数(GCD)是指两个或多个整数共有约数中最大的一个。例如,8 和 12 的最大公约数是 4,因为 4 是能同时整除 8 和 12 的最大整数。
辗转相除法的基本思想是:
- 对于两个正整数 a 和 b(a > b),用 a 除以 b 得到余数 r
- 如果 r = 0,则 b 就是最大公约数
- 如果 r ≠ 0,则以 b 和 r 为新的两个数,重复上述过程,直到余数为 0
- 最后一个非零余数就是原来两个数的最大公约数
此外,需要考虑以下特殊情况: - 如果其中一个数为 0,则最大公约数是另一个非零数如果两个数都是 0,则最大公约数无定义(通常返回 0)
- 负数的最大公约数与它们的绝对值的最大公约数相同
思路实现设计
1.循环结构实现(GreatestCommonDivisor 函数):
- 处理负数:将输入的 a 和 b 转换为它们的绝对值
- 处理边界情况:如果 b 为 0,则返回 a
- 循环计算:当 b 不为 0 时,计算 a 除以 b 的余数 r,然后将 b 赋值给 a,将 r 赋值给 b
- 循环结束时,a 的值就是最大公约数
2.递归结构实现(gcd 函数): - 处理负数:将输入的 a 和 b 转换为它们的绝对值
- 递归基线条件:如果 b 为 0,则返回 a
- 递归调用:否则返回 gcd (b, a % b)
3.测试数据设计: - 两个正整数,如 (8, 12)
- 包含一个负数,如 (18, -12)
- 两个数成倍数关系,如 (15, 45)
- 两个质数,如 (7, 13)
代码
#include <iostream>
#include <cstdlib>
using namespace std;// 1. 循环结构
int GreatestCommonDivisor(int a, int b) {// 处理负数(GCD结果恒为正数)a = abs(a);b = abs(b);// 辗转相除法核心循环:b不为0时持续迭代while (b != 0) {int remainder = a % b; // a除以b的余数a = b; // 更新a为当前除数bb = remainder; // 更新b为余数,进入下一轮计算}return a; // 当b=0时,a为最大公约数
}// 2. 递归方式
int gcd(int a, int b) {// 处理负数,转为非负值a = abs(a);b = abs(b);// 递归基线条件:b为0,返回a(此时a为最大公约数)if (b == 0) {return a;} else {// 递归调用return gcd(b, a % b);}
}
int main() {int num1, num2;cout << "请输入两个整数:";cin >> num1 >> num2;// 调用循环结构函数int result1 = GreatestCommonDivisor(num1, num2);// 调用递归结构函数int result2 = gcd(num1, num2);cout << "循环法计算的最大公约数:" << result1 << endl;cout << "递归法计算的最大公约数:" << result2 << endl;return 0;
}
代码解析
1.循环结构实现(GreatestCommonDivisor 函数):
- 首先使用abs函数将输入的 a 和 b 转换为绝对值,以处理负数情况
- 使用while循环进行辗转相除:
- 计算 a 除以 b 的余数remainder
- 将 b 的值赋给 a,将余数的值赋给 b
- 当 b 变为 0 时,循环结束,此时 a 的值就是最大公约数
- 返回 a 作为结果
2.递归结构实现(gcd 函数):
- 同样先将 a 和 b 转换为绝对值
- 递归的基线条件:如果 b 为 0,则返回 a 作为结果
- 递归调用:否则返回gcd(b, a % b),体现了辗转相除法的核心思想
3.测试函数(testGCD):
- 接收两个整数作为参数
- 分别调用循环法和递归法计算最大公约数
- 输出测试数据和两种方法的计算结果
- 验证两种方法的结果是否一致
4.主函数(main):
- 预设了 8 组测试数据,涵盖了各种情况
- 调用 testGCD 函数对每组数据进行测试
- 提供用户交互部分,允许用户输入两个整数并计算它们的最大公约数
- 输出两种方法的计算结果
运行截图
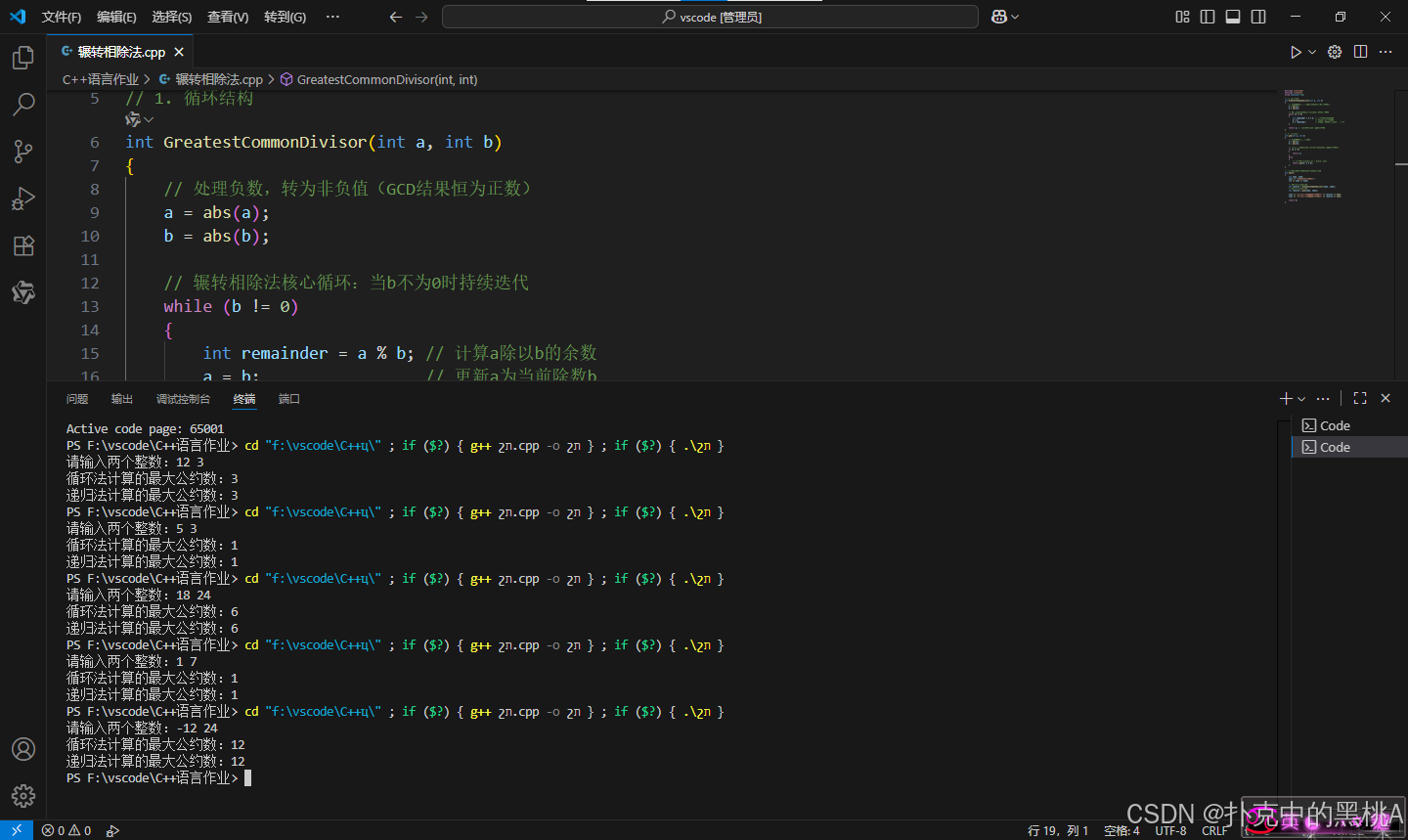
结果分析
- 两种实现方法(循环和递归)对于所有测试数据都能得到相同的结果
- 程序能够正确处理正数、负数和零的各种组合情况
- 对于较大的整数,算法仍然能够高效地计算出结果
- 递归实现没有出现栈溢出的情况,说明算法的递归深度是可控的
3、最小公倍数
函数重载求解最小公倍数lcm(Least Common Multiple)。实现以下函数以求解2、3、4个整数的最小公倍数,并使用3组对应数量的数据进行测试。
int lcm(int a, int b);
int lcm(int a, int b, int c);
int lcm(int a, int b, int c, int d);
基本思路
最小公倍数与最大公约数之间存在密切的数学关系:对于两个正整数 a 和 b,它们的最小公倍数等于它们的乘积除以它们的最大公约数,即:
LCM(a, b) = |a × b| / GCD(a, b)
这个公式是计算最小公倍数的基础。对于多个数的最小公倍数,可以通过逐步计算的方式得到:
- 三个数的最小公倍数:LCM (a, b, c) = LCM (LCM (a, b), c)
- 四个数的最小公倍数:LCM (a, b, c, d) = LCM (LCM (a, b, c), d)
需要考虑的特殊情况:
- 如果其中一个数为 0,则最小公倍数为 0
- 负数的最小公倍数与它们的绝对值的最小公倍数相同
思路实现设计
1.最大公约数计算:
复用之前实现的循环结构的最大公约数函数GreatestCommonDivisor
2.两个数的最小公倍数(lcm 函数):
- 处理负数:将输入的 a 和 b 转换为它们的绝对值
- 处理特殊情况:如果其中一个数为 0,则返回 0
- 应用公式:LCM (a, b) = (a × b) / GCD (a, b)
3.三个数的最小公倍数(重载 lcm 函数): - 先计算前两个数的最小公倍数
- 再计算结果与第三个数的最小公倍数
- 即:lcm (a, b, c) = lcm (lcm (a, b), c)
4.四个数的最小公倍数(重载 lcm 函数): - 先计算前三个数的最小公倍数
- 再计算结果与第四个数的最小公倍数
- 即:lcm (a, b, c, d) = lcm (lcm (a, b, c), d)
5.测试数据设计: - 两个数的情况:如 (4, 6)、(5, 7)、(0, 5)
- 三个数的情况:如 (2, 3, 4)、(6, 8, 12)、(5, 0, 10)
- 四个数的情况:如 (2, 3, 4, 5)、(3, 6, 9, 12)、(7, 14, 21, 28)
代码
#include <iostream>
#include <cstdlib>
#include <vector>
using namespace std;// 最大公约数计算
int GreatestCommonDivisor(int a, int b)
{a = abs(a);b = abs(b);while (b != 0){int remainder = a % b;a = b;b = remainder;}return a;
}// 2个整数的最小公倍数
int lcm(int a, int b)
{a = abs(a);b = abs(b);return (a == 0 || b == 0) ? 0 : (a * b) / GreatestCommonDivisor(a, b);
}// 3个整数的最小公倍数(重载)
int lcm(int a, int b, int c)
{return lcm(lcm(a, b), c);
}// 4个整数的最小公倍数(重载)
int lcm(int a, int b, int c, int d)
{return lcm(lcm(a, b, c), d);
}int main()
{vector<int> nums; // 存储输入的整数int num;cout << "请输入2-4个整数(用空格分隔,回车结束):";// 读取输入的所有整数,直到回车或输入错误while (cin >> num) // ctrl+Z 结束{nums.push_back(num);// 输入数量超过4个,立刻停止读取if (nums.size() >= 4)break;}// 判断输入的数量来调用对应函数switch (nums.size()){case 2:cout << "最小公倍数:" << lcm(nums[0], nums[1]) << endl;break;case 3:cout << "最小公倍数:" << lcm(nums[0], nums[1], nums[2]) << endl;break;case 4:cout << "最小公倍数:" << lcm(nums[0], nums[1], nums[2], nums[3]) << endl;break;default:cout << "输入错误!请输入2-4个整数。" << endl;}return 0;
}
代码解析
1.最大公约数函数(GreatestCommonDivisor):
- 复用之前实现的循环结构的最大公约数计算函数
- 用于支持最小公倍数的计算
2.两个数的最小公倍数函数(lcm):
- 首先将输入的 a 和 b 转换为绝对值,处理负数情况
- 检查是否有 0,如果有则返回 0
- 应用公式计算并返回最小公倍数:(a * b) / GCD (a, b)
3.三个数的最小公倍数函数(重载 lcm):
- 利用两个数的 lcm 函数,先计算前两个数的最小公倍数
- 再计算该结果与第三个数的最小公倍数
- 体现了多个数的最小公倍数可以通过逐步计算得到的思想
4.四个数的最小公倍数函数(重载 lcm):
- 利用三个数的 lcm 函数,先计算前三个数的最小公倍数
- 再计算该结果与第四个数的最小公倍数
- 进一步扩展了最小公倍数的计算能力
5.测试函数:
- testLCM2:测试两个数的最小公倍数计算
- testLCM3:测试三个数的最小公倍数计算
- testLCM4:测试四个数的最小公倍数计算
- 每个测试函数都输出输入数据和计算结果
6.主函数(main):
- 预设了多组测试数据,涵盖不同情况
- 调用测试函数对预设数据进行测试
- 提供用户交互部分,允许用户输入 2-4 个整数
- 根据用户输入的整数数量,调用相应的 lcm 函数并输出结果
运行截图
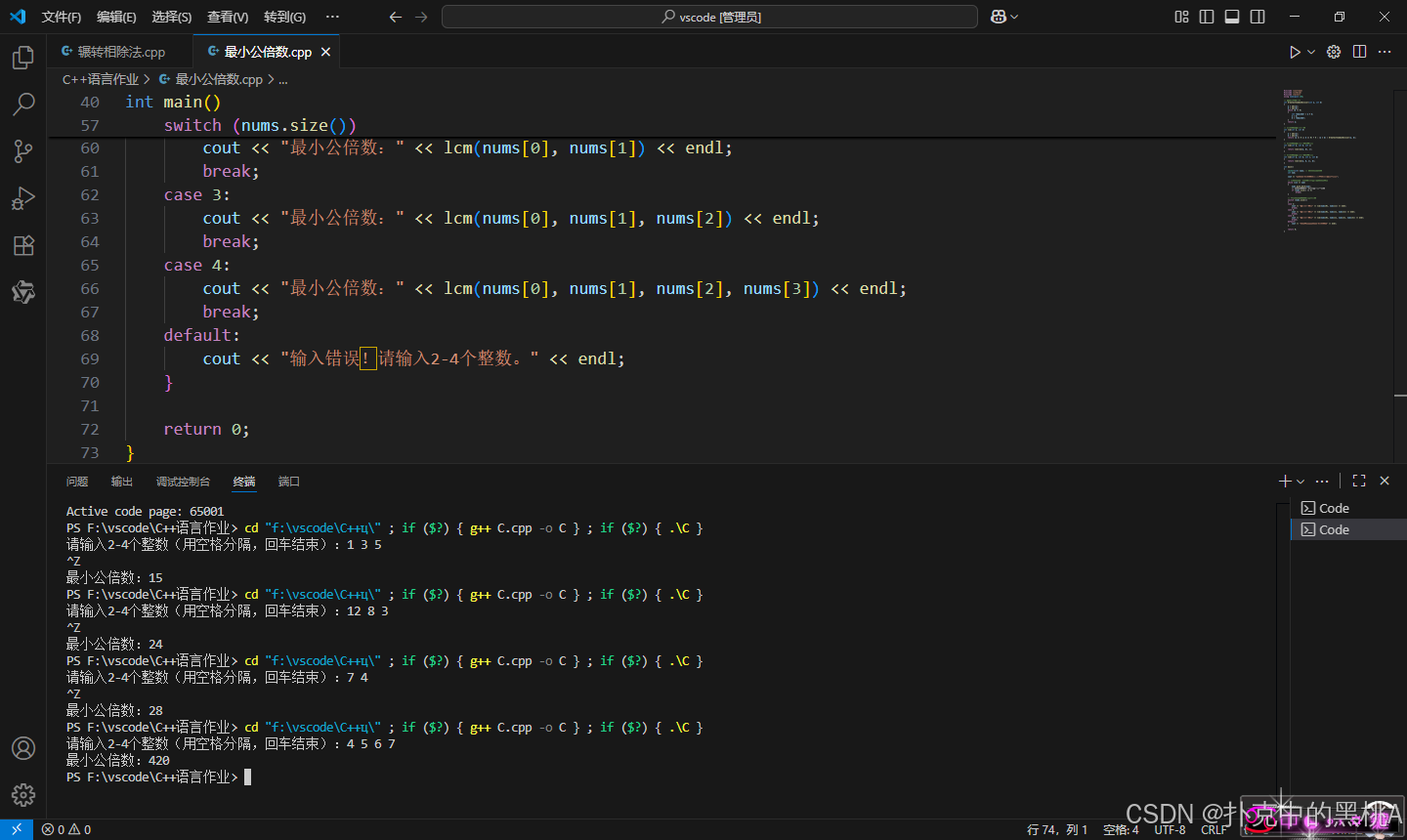
结果分析
- 函数重载工作正常,根据参数数量的不同,调用了相应的函数
- 所有测试案例的计算结果都符合预期
- 程序能够正确处理包含负数和零的情况
- 多参数的最小公倍数计算通过逐步计算的方式实现,逻辑正确
总结
通过本次实验,我深入理解和掌握了 C++ 函数的相关知识和应用技巧,具体包括以下几个方面:
1.函数的基本应用:
- 掌握了函数的定义、声明和调用方法
- 学会了通过函数参数传递数据和通过返回值获取结果
- 理解了函数的封装性,将特定功能封装到函数中,提高了代码的复用性和可读性
2.函数默认参数:
- 在水仙花数判断函数中使用了默认参数,使函数调用更加灵活
- 理解了默认参数的使用规则,如默认参数必须放在参数列表的后面
3.递归函数:
- 实现了递归版本的最大公约数计算函数
- 深入理解了递归的基本思想:将大问题分解为小问题,通过解决小问题来解决大问题
- 掌握了递归函数的设计要点:必须有明确的基线条件,避免无限递归
4.函数重载:
- 通过函数重载实现了计算 2、3、4 个整数的最小公倍数
- 理解了函数重载的概念:允许有多个同名函数,只要它们的参数列表不同
- 体会到函数重载带来的好处:提高了代码的可读性和易用性,体现了多态性
5.算法设计与实现:
- 学会了分析问题并设计相应的算法
- 掌握了自幂数判断、辗转相除法、最小公倍数计算等经典算法
- 学会了设计测试用例,验证算法的正确性在实验过程中,我也遇到了
6.一些问题和挑战:
- 边界情况处理:如处理 0、负数等特殊情况,需要仔细考虑算法的正确性
- 递归深度控制:在实现递归函数时,需要确保有正确的基线条件,避免栈溢出
- 函数重载的使用:需要注意参数列表的差异,确保重载函数能够被正确调用
通过解决这些问题,我的编程能力和问题分析能力得到了提升。同时,我也认识到编写健壮的程序需要考虑各种可能的情况,不仅要使程序在正常情况下工作,还要能处理各种异常情况。
