从零开始学二叉树(中):堆与完全二叉树的奥秘
目录
🌟 引言:从“家谱树”到“堆”——结构变了,效率高了
1️⃣ 二叉树:有序的“两孩家庭”
2️⃣ 满二叉树 vs 完全二叉树:名字只差一字,结构大不同
🔹 满二叉树(Full Binary Tree)
🔹 完全二叉树(Complete Binary Tree)
🤔 为什么完全二叉树这么重要?
3️⃣ 完全二叉树 + 数组 = 天作之合
神奇的索引公式(必须背!)
4️⃣ 堆:完全二叉树 + 特殊性质 = 高效优先队列
🔸 什么是堆?
🔸 堆的操作核心:调整算法
(1)向上调整(Insert 用)
(2)向下调整(Delete 用)
5️⃣ 建堆:向上 vs 向下,谁更快?
❓ 问题:给一个无序数组,如何快速建成堆?
📊 复杂度分析(关键!)
6️⃣ 堆的应用一:堆排序(Heap Sort)
🔸 思路
📝 C 代码实现(高效版):
7️⃣ 堆的应用二:Top-K 问题(面试高频!)
🔍 问题描述
🤯 为什么用“小堆”找“前 K 大”?
步骤:
📝 C 代码框架(简化版):
✅ 本篇小结
💡 思考题(动手更深刻!)
📢 下期预告:《从零开始学二叉树(下):链式二叉树与递归的终极修炼》
作者:一位曾把“小顶堆”写成“大顶堆”、调了两小时才意识到的计算机学生
目标读者:刚搞懂树基本概念、准备深入二叉树的大一/大二同学
一句话预告:为什么完全二叉树能用数组存?堆排序为什么快?Top-K 问题为何反直觉地用小堆?
🌟 引言:从“家谱树”到“堆”——结构变了,效率高了
上一篇,我们用文件系统理解了“树”的本质:层次 + 分支。
但如果你真用链表把每个文件夹、文件都连起来,内存开销大不说,找一个文件可能得遍历半天。
有没有一种结构规整、存储紧凑、操作高效的树?
有!它就是——完全二叉树,而它的明星应用,叫做 堆(Heap)。
今天,我们就揭开堆的神秘面纱:
- 为什么完全二叉树能用数组完美表示?
- 堆到底是个啥?为什么插入、删除只要 O(log n)?
- Top-K 问题中,“前 K 大用小堆”到底是什么反直觉操作?
- 为什么建堆用向下调整比向上调整更快?
别怕,我们一步步来,用生活例子 + C 代码 + 手动模拟,让你彻底搞懂!

1️⃣ 二叉树:有序的“两孩家庭”
先快速回顾:二叉树 ≠ 任意树。
它的两大特点:
- 每个结点最多两个孩子(左、右)
- 左右有严格顺序,不能互换 → 这是有序树
✅ 举个反例:
如果你把“左子树”和“右子树”位置随便换,那前序/中序遍历结果就变了!
所以——二叉树的结构信息藏在“左右顺序”里。
2️⃣ 满二叉树 vs 完全二叉树:名字只差一字,结构大不同
🔹 满二叉树(Full Binary Tree)
定义:每一层的结点数都达到最大值。
深度为 h 的满二叉树,总共有 2h−1 个结点。
比如深度为 3 的满二叉树:
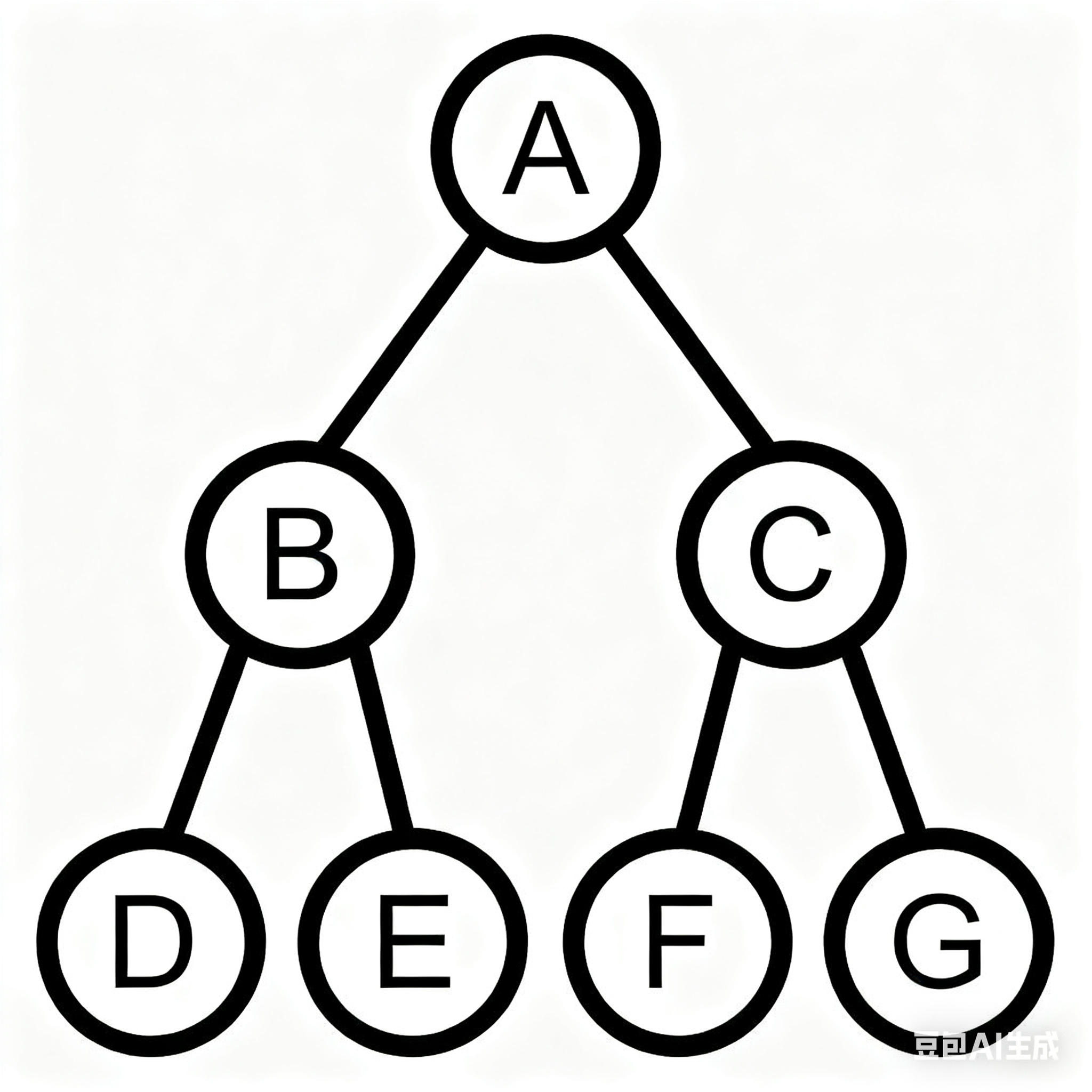
- 第 1 层:1 个(20 )
- 第 2 层:2 个(21 )
- 第 3 层:4 个(22 )
- 总结点:1+2+4 = 7 = 23−1
📌 特点:完美对称,没有“缺胳膊少腿”。
🔹 完全二叉树(Complete Binary Tree)
定义:
深度为 h 的树,前 h-1 层是满的,第 h 层结点“靠左连续排列”,中间不能有空缺。
✅ 正确例子(完全二叉树):
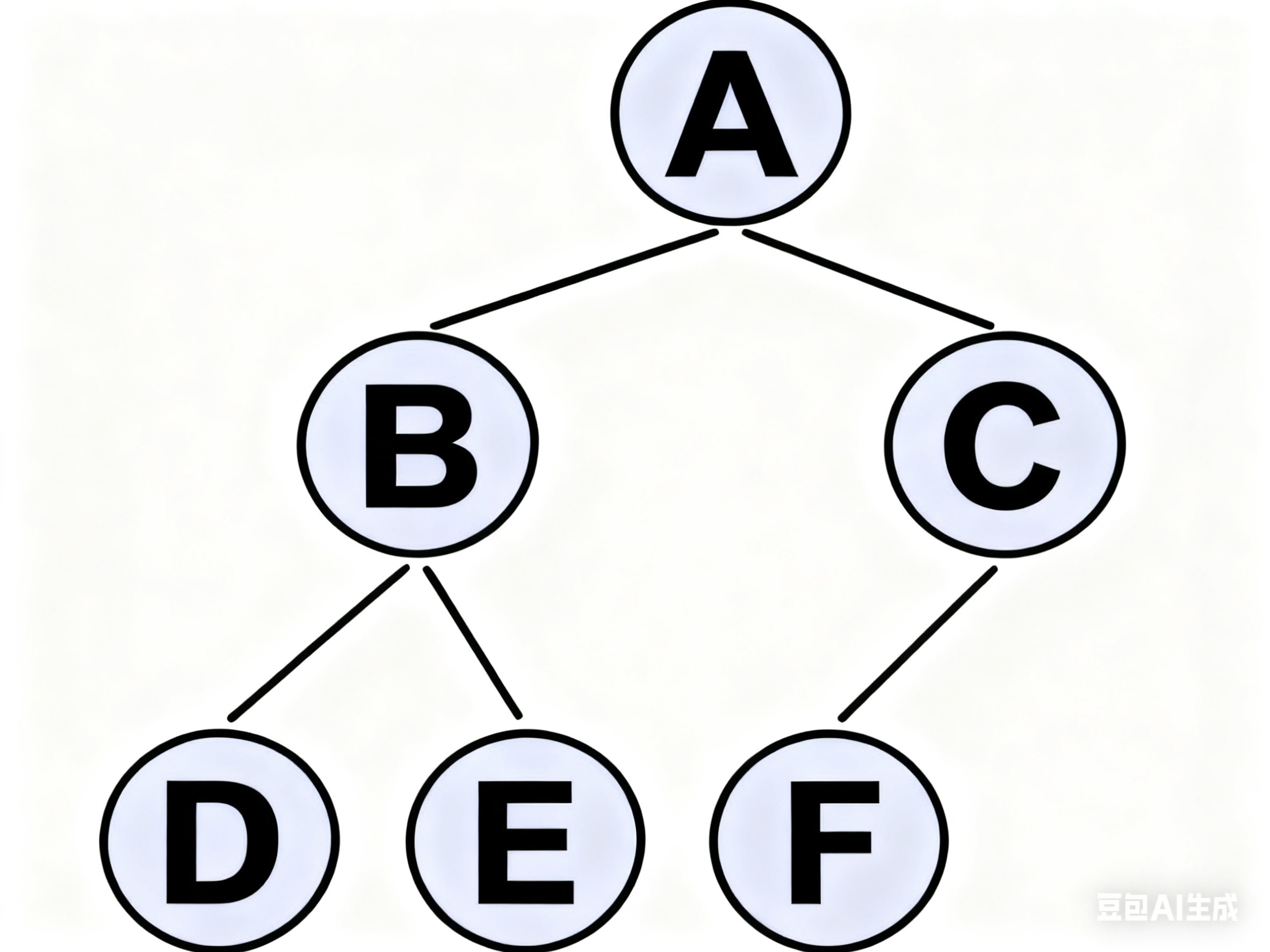
- 第 3 层:F 紧挨着 E,左边没有空
❌ 非完全二叉树:
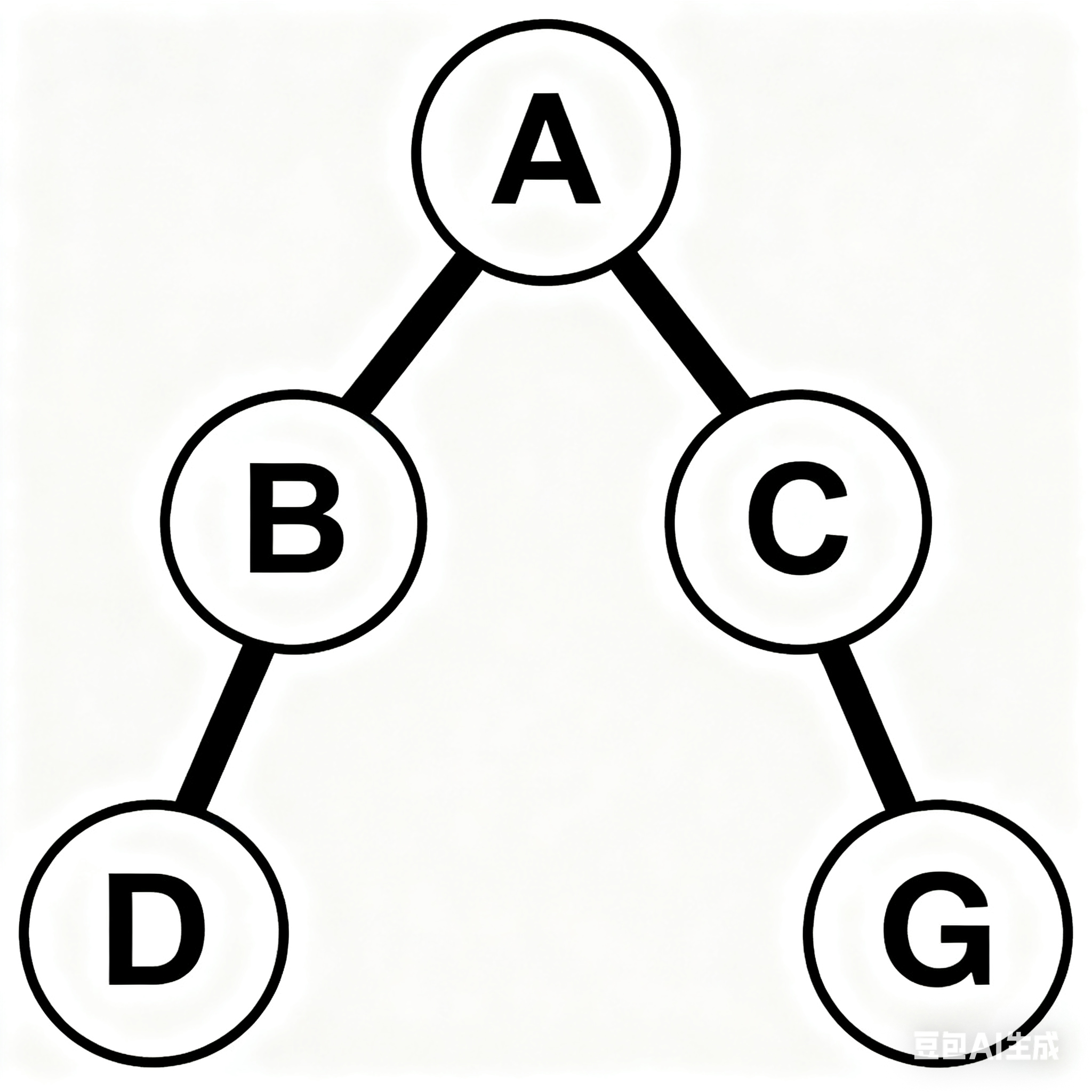
💡 关键理解:
“完全” = 尽可能满,且最后一层靠左。
→ 满二叉树是特殊的完全二叉树。
🤔 为什么完全二叉树这么重要?
因为它可以用数组高效存储!而普通二叉树用数组会浪费大量空间。
3️⃣ 完全二叉树 + 数组 = 天作之合
神奇的索引公式(必须背!)
假设我们用数组从 0 开始编号,存储一棵完全二叉树:
| i |
|
|
|
🔍 推导逻辑(理解比死记更重要):
- 根结点 i=0 → 父结点不存在(i=0 时
(0-1)/2是负数,忽略)- i=1(B) → 父 = (1-1)/2 = 0(A),左孩 = 2×1+1=3(D),右孩=4(E)
- i=2(C) → 父 = (2-1)/2 = 0(整除),左孩=5(F)
✅ 例子验证: 数组:[A, B, C, D, E, F]
对应树:
A(0)
/ \
B(1) C(2)
/ \ /
D(3) E(4) F(5)
完全匹配!
📌 重要结论:
只有完全二叉树才能用数组无浪费存储父子关系。
普通树用数组会有大量“空洞”,比如空指针占位。
4️⃣ 堆:完全二叉树 + 特殊性质 = 高效优先队列
🔸 什么是堆?
堆是一种特殊的完全二叉树,满足:
- 大根堆:任意结点 ≥ 其孩子 → 根最大
- 小根堆:任意结点 ≤ 其孩子 → 根最小
✅ 大根堆例子(数组表示):
数组:[90, 80, 70, 60, 50, 40]
树形:
90
/ \
80 70
/ \ /
60 50 40
- 90 ≥ 80, 70
- 80 ≥ 60, 50
- 70 ≥ 40
→ 满足大根堆性质!
🔸 堆的操作核心:调整算法
堆的插入/删除,本质是破坏堆性质 → 调整恢复。
(1)向上调整(Insert 用)
场景:在数组末尾插入一个新元素(比如插入 95 到大根堆)
步骤:
- 把 95 放到数组末尾 →
[90,80,70,60,50,40,95] - 95 的父 = (6-1)/2 = 2 → 70
- 95 > 70 → 交换 →
[90,80,95,60,50,40,70] - 新位置 i=2,父=(2-1)/2=0 → 90
- 95 > 90 → 交换 →
[95,80,90,60,50,40,70] - 到根了,停止!
✅ C 代码实现:
void AdjustUp(HPDataType* a, int child) {int parent = (child - 1) / 2;while (child > 0) {if (a[child] > a[parent]) { // 大根堆:孩子 > 父?Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;} else {break; // 已满足堆性质}}
}void HPPush(HP* php, HPDataType x) {// 数组扩容(略)php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1); // 从最后一个元素向上调整
}📌 时间复杂度:O(log n) —— 最多从叶子走到根,走树高。
(2)向下调整(Delete 用)
前提:左右子树已经是堆(插入不满足,但删除时满足!)
场景:删除堆顶(90),常规做法:
- 把最后一个元素(40)换到堆顶 →
[40,80,70,60,50] - 40 和左右孩子比:左=80,右=70 → 80 最大
- 40 < 80 → 交换 →
[80,40,70,60,50] - 新位置 i=1,左=60,右=50 → 60 最大
- 40 < 60 → 交换 →
[80,60,70,40,50] - 到叶子了,停止!
✅ C 代码实现:
void AdjustDown(HPDataType* a, int n, int parent) {int child = parent * 2 + 1; // 先假设左孩子while (child < n) {// 选左右孩子中更大的(大根堆)if (child + 1 < n && a[child + 1] > a[child]) {child++; // 右孩子更大}if (a[child] > a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;} else {break;}}
}void HPPop(HP* php) {Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a, php->size, 0); // 从根向下调整
}5️⃣ 建堆:向上 vs 向下,谁更快?
❓ 问题:给一个无序数组,如何快速建成堆?
两种思路:
| 逐个插入(向上调整) | 从空堆开始,一个个 HPPush | O(n log n) |
| 整体调整(向下调整) | 从最后一个非叶子结点开始,倒着 AdjustDown | O(n) |
✅ 为什么向下调整建堆更快?
📊 复杂度分析(关键!)
-
向上调整建堆:
向上调整算法建堆时间复杂度为:O(n ∗ log2 n) -
向下调整建堆:
- 底层结点多,但移动距离短(叶子不用调)
- 顶层结点少,但移动距离长
- 数学证明总和是 O(n)
💡 代码实现(向下建堆):
// 从最后一个非叶子结点开始调整
// 最后一个结点索引 = n-1 → 父 = (n-2)/2 = (n-1-1)/2
for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, n, i);
}📌 踩坑经历:
我第一次写堆排序,用的是“逐个插入建堆”,数据一多直接超时。
后来换成“向下调整建堆”,瞬间快了 10 倍!
记住:建堆用向下调整,别用插入!
6️⃣ 堆的应用一:堆排序(Heap Sort)
🔸 思路
- 建大根堆(升序)
- 把堆顶(最大值)和最后一个元素交换
- 堆大小减 1,对新堆顶向下调整
- 重复 2~3,直到堆只剩一个元素
✅ 原地排序:不需要额外数据结构,直接在原数组操作!
📝 C 代码实现(高效版):
void HeapSort(int* a, int n) {// 建大堆(O(n))for (int i = (n - 1 - 1) / 2; i >= 0; i--) {AdjustDown(a, n, i);}// 排序(O(n log n))int end = n - 1;while (end > 0) {Swap(&a[0], &a[end]); // 最大值放到末尾AdjustDown(a, end, 0); // 对 [0, end) 重新堆化end--;}
}✅ 时间复杂度:O(n) + O(n log2 n) = O(n log2 n)
✅ 空间复杂度:O(1) —— 原地排序!
7️⃣ 堆的应用二:Top-K 问题(面试高频!)
🔍 问题描述
从 100 万个数中,找出最大的前 10 个数。
❌ 暴力法:排序 → O(n log n),而且可能内存装不下!
✅ 堆解法:建小堆,存前 K 大!
🤯 为什么用“小堆”找“前 K 大”?
核心思想:
我们只关心“是不是比当前第 K 大的数更大”。
小堆的堆顶是最小值,正好代表“当前第 K 大的门槛”。
步骤:
- 取前 K 个数,建小根堆 → 堆顶是这 K 个中最小的
- 遍历剩下的 N-K 个数:
- 如果 x > 堆顶 → 说明 x 有资格进前 K
- 把堆顶换成 x,再向下调整
- 最终堆中就是前 K 大的数
✅ 优势:
- 内存只用存 K 个数(K << N)
- 时间复杂度:O(K) + O((N-K) log2 K) ≈ O(N log2 K)
📝 C 代码框架(简化版):
void TopK(int* data, int n, int k) {int* minheap = (int*)malloc(sizeof(int) * k);// 1. 取前k个,建小堆for (int i = 0; i < k; i++) minheap[i] = data[i];for (int i = (k - 2) / 2; i >= 0; i--) AdjustDownMin(minheap, k, i); // 注意:这里是小堆版 AdjustDown// 2. 遍历剩余元素for (int i = k; i < n; i++) {if (data[i] > minheap[0]) {minheap[0] = data[i];AdjustDownMin(minheap, k, 0);}}// 输出结果for (int i = 0; i < k; i++) printf("%d ", minheap[i]);free(minheap);
}💡 小堆 AdjustDown 需要改比较方向(孩子 < 父才交换)
✅ 本篇小结
| 完全二叉树 | 最后一层靠左连续,可用数组无浪费存储 |
| 父子索引公式 |
|
| 堆 | 完全二叉树 + 堆性质(大根/小根) |
| 向上调整 | 插入用,O(log n) |
| 向下调整 | 删除 & 建堆用,建堆总体 O(n) |
| 堆排序 | 建堆 + 首尾交换 + 向下调整 |
| Top-K | 前 K 大 → 小堆,内存省、效率高 |
💡 思考题(动手更深刻!)
- 画图:用数组
[10, 20, 15, 30, 40]画出对应的完全二叉树,并标出每个结点的父子关系。 - 手算:对数组
[3,1,4,1,5,9,2]执行“向下调整建大堆”,写出每一步调整后的数组。 - 反直觉挑战:为什么“前 K 小”要用大堆?试着用逻辑解释。
- 代码改错:下面这段小堆的
AdjustDown有什么问题?
if (child + 1 < n && a[child + 1] > a[child]) // 小堆用 >📢 下期预告:《从零开始学二叉树(下):链式二叉树与递归的终极修炼》
我们将深入:
- 链式二叉树如何手动构建?
- 前/中/后序遍历的递归本质是什么?(附栈帧图解)
- 如何根据遍历结果反推树结构?
- 层序遍历 + 判断完全二叉树的队列实现
- LeetCode 入门题思路引导:单值树、对称树…
🌟 终极目标:让你看到树,就想到递归;写递归,就想到树!
📣 小寄语:
堆不是“堆内存”,而是一种精巧的结构设计。
它告诉我们:规则带来效率,结构决定性能。
下次你在游戏里看到“战力排行榜前 10”,
就知道——背后很可能是一个小堆在默默工作!
欢迎在评论区晒出你的思考题答案,或分享你在堆排序/Top-K 上的踩坑经历!
👉 点赞 + 收藏 + 关注,三连不迷路!
感谢各位的观看




