锥优化介绍(2025年9月27日)
锥优化介绍(2025年9月27日)
本文节选自B站视频《第3讲-锥规划及其在能源系统优化中的应用 Part I》,鸣谢北交电气许老师。以下将本人理解部分写出,以供参考。
基本概念
凸集
集合内部任意两个点连成线段,线段上的点都在集合中。
对任意的x1x_1x1,x2∈Cx_2\in\mathbb{C}x2∈C 以及0≤θ≤10\leq\theta\leq10≤θ≤1,有θx1+(1−θ)x2∈C\theta x_1 + (1-\theta) x_2 \in \mathbb{C}θx1+(1−θ)x2∈C
举例:
- {x∣aTx=b},a∈Rn,a≠0,b∈R\{x|a^T x = b\}, a\in \mathbb{R}^n, a\neq0, b\in \mathbb{R}{x∣aTx=b},a∈Rn,a=0,b∈R 线性等式,是凸集
- {x∣aTx≤b},a∈Rn,a≠0,b∈R\{x|a^T x \leq b\}, a\in \mathbb{R}^n, a\neq0, b\in \mathbb{R}{x∣aTx≤b},a∈Rn,a=0,b∈R 半空间,是凸集
- {x∣(x−xc)TP−1(x−xc)≤1},P∈S++n\{x|(x-x_c)^T P^{-1}(x-x_c)\leq1\}, P\in S^n_{++}{x∣(x−xc)TP−1(x−xc)≤1},P∈S++n 椭球,正定,是凸集
- {x∣ajTx≤bj,j=1,⋯,m,cjTx=dj,j=1,⋯,p}\{x|a_j^T x \leq b_j, j=1,\cdots, m,c_j^T x = d_j, j=1,\cdots, p \}{x∣ajTx≤bj,j=1,⋯,m,cjTx=dj,j=1,⋯,p} 多面体,是凸集
- {Ax+b∣x∈S}\{A\mathbf{x}+b | \mathbf{x}\in \mathbf{S}\}{Ax+b∣x∈S} 其中,S\mathbf{S}S是凸集,为对S\mathbf{S}S做线性变换, 仍是凸集
- {x∣xTAX+bTx+c=0},A∈Sn,b∈Rn,A≠0\{x|x^TAX+b^Tx+c=0\}, A\in S^n, b\in R^n, A\neq0{x∣xTAX+bTx+c=0},A∈Sn,b∈Rn,A=0 不是凸集。非线性的等式约束都不是凸集
凸包
若集合不是凸集,则将所有最外围的点包络起来形成一个凸集的形状,称为凸包
锥
一个集合是一个锥,则对于任一点x∈Sx\in\mathbf{S}x∈S, 对θ≥0\theta\geq0θ≥0, 均有θx∈C\theta x \in \mathbf{C}θx∈C。锥中满足凸集条件的称为凸锥。
二阶锥
范数锥。满足条件:
{(x,t)∣∣∣x∣∣2≤t}={[xt][100−1][xt]≤0,t≤0,x∈Rn,t∈R}\{(x, t)|\left\lvert\lvert x\right\rvert\rvert_2\leq t\}=\left\{\left[ \begin{array}{l} x&t \end{array} \right] \left[ \begin{array}{c} 1&0\\ 0&-1 \end{array} \right] \left[ \begin{array}{c} x\\t \end{array} \right]\leq0, t\leq 0, x\in \mathbb{R}^n, t\in R \right\} {(x,t)∣∣∣x∣∣2≤t}={[xt][100−1][xt]≤0,t≤0,x∈Rn,t∈R}
即空间中,
[x1x2⋮xnt]\left[ \begin{array}{c} x_1\\x_2\\ \vdots \\ x_n \\ t \end{array} \right] x1x2⋮xnt
[x1x2⋮xn]\left[ \begin{array}{c} x_1\\x_2\\ \vdots \\ x_n \end{array} \right]x1x2⋮xn的范数小于ttt(在不在最后不重要)
值得注意的是,二阶锥是凸锥。其更常用的形式:
∥Ax+b∥2≤cTx+d⇔[AcT]x+[bd]∈{[ut]∣∥u∥2≤t}\left\lVert Ax+b\right \rVert_2\leq c^Tx+d \Leftrightarrow \left[\begin{array}{c} A\\c^T \end{array}\right]x + \left[\begin{array}{c} b\\d \end{array}\right]\in \{ \left[\begin{array}{c} u\\t \end{array}\right]\vert \left\Vert u \right\Vert_2\leq t \} ∥Ax+b∥2≤cTx+d⇔[AcT]x+[bd]∈{[ut]∣∥u∥2≤t}
二阶锥有两种形式。
第一种形式:x22+x32≤x1\sqrt{x_2^2 + x_3^2} \leq x_1x22+x32≤x1
第二种形式: x32≤2x1x2,x1,x2≥0x_3^2\leq 2x_1x_2, x_1, x_2 \geq 0x32≤2x1x2,x1,x2≥0
举例:
给定x∈Rn,y,z∈Rx\in R^n, y,z\in Rx∈Rn,y,z∈R验证x,y,zx, y, zx,y,z 满足:xTx≤yz,y≥0,z≥0x^Tx\leq yz, y\geq0, z\geq0xTx≤yz,y≥0,z≥0,当且仅当∥[2xy−z]∥2≤y+z,y≥0,z≥0\left\Vert\left[\begin{array}{c}2x\\y-z\end{array}\right]\right\Vert_2\leq y+z, y\geq0, z\geq0[2xy−z]2≤y+z,y≥0,z≥0
答案:可直接通过2范数的定义完成验证
凸优化
凸优化(Convex Optimization)
minf0(x)s.t.fi(x)≤0i=1,⋯,maiTx=bii=1,⋯,p\begin{equation} \begin{aligned} & \min \quad f_0(x)\\ &\begin{array}{l} s.t. & f_i(x) \leq 0 \quad i = 1, \cdots, m\\ & a^T_ix = b_i \quad i = 1, \cdots , p \\ \end{array} \end{aligned} \end{equation} minf0(x)s.t.fi(x)≤0i=1,⋯,maiTx=bii=1,⋯,p
其中,f0(x)f_0(x)f0(x)和fi(x)f_i(x)fi(x)均为凸函数;对于任何一个凸优化问题而言,其局部最优解已经是全局最优解。
二阶锥规划
二阶锥规划(Second Order Cone Programming)
minfTxs.t.∥Aix+bi∥≤ciTx+di,i=1,⋯,mFx=g\begin{equation} \begin{aligned} &\min \quad f^Tx\\ & \begin{array}{l} s.t. &\left\Vert A_ix+b_i\right\Vert \leq c_i^Tx+d_i, i=1,\cdots, m\\ & Fx=g \end{array} \end{aligned} \end{equation} minfTxs.t.∥Aix+bi∥≤ciTx+di,i=1,⋯,mFx=g
二阶锥规划为一个凸优化问题,可使用求解器解决。因此,如将物理系统建模为二阶锥规划问题,则问题可视为已解决。
应用案例
电力系统最优潮流
电力系统最优潮流(Optimal Power Flow)。给定电力系统的结构参数和负荷情况,调节可以利用的控制变量,如发电机输出功率、变压器分接头挡位、电容和电抗的接入。
从而找到一个潮流分布,满足系统的运行约束条件,使发电成本最低或系统的网损最小。
在其中过程中,满足节点电压约束、支路的电流、功率约束,以及发电机功率约束等约束条件。
电力系统最优潮流模型
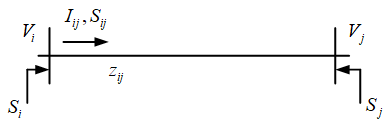
电力系统最优潮流模型如下所示:
min∑i∈Ncipigs.t.潮流方程V‾i≤∣Vi∣≤V‾i,∀i∈N节点电压约束S‾ig≤Sig≤S‾ig,∀i∈N发电机功率约束∣Iij∣≤I‾ij,∀(i,j)∈ϵ线路电流约束\begin{equation} \begin{aligned} &\min \quad \sum_{i\in N}c_ip_i^g\\ & \begin{array}{l} s.t. & 潮流方程\\ & \underline{V}_i\leq |V_i| \leq \overline{V}_i, \quad \forall i\in\N \quad 节点电压约束\\ & \underline{S}_i^g\leq S_i^g \leq \overline{S}_i^g , \quad \forall i\in\N \quad 发电机功率约束\\ & |I_ij|\leq \overline{I}_{ij}, \quad \forall (i,j)\in\mathbb{\epsilon} \quad 线路电流约束 \end{array} \end{aligned} \end{equation} mini∈N∑cipigs.t.潮流方程Vi≤∣Vi∣≤Vi,∀i∈N节点电压约束Sig≤Sig≤Sig,∀i∈N发电机功率约束∣Iij∣≤Iij,∀(i,j)∈ϵ线路电流约束
其中,潮流方程包括以下式子:
Vi−Vj=zijIij∀(i,j)∈ϵ欧姆定律Sij=ViIij∗∀(i,j)∈ϵ支路首端功率∑k:j→kSjk−∑k:i→j(Sij−zij∣Iij∣2)=sj∀(i,j)∈ϵ节点功率平衡\begin{align} & V_i -V_j =z_{ij}I_{ij} \quad \forall(i,j)\in \epsilon \quad 欧姆定律\\ & S_{ij} = V_i I_{ij}^* \quad \forall(i,j)\in \epsilon \quad 支路首端功率\\ & \sum_{k:j\rightarrow k}S_{jk}-\sum_{k:i\rightarrow j}(S_{ij}-z_{ij}|I_{ij}|^2 )=s_j\quad \forall(i,j)\in \epsilon \quad 节点功率平衡 \end{align} Vi−Vj=zijIij∀(i,j)∈ϵ欧姆定律Sij=ViIij∗∀(i,j)∈ϵ支路首端功率k:j→k∑Sjk−k:i→j∑(Sij−zij∣Iij∣2)=sj∀(i,j)∈ϵ节点功率平衡
其中变量包括{Sij}\{S_{ij}\}{Sij}, {Iij}\{I_{ij}\}{Iij}, {Vi}\{V_{i}\}{Vi}, {si}\{s_i\}{si}
由于潮流方程中的支路首端功率和节点功率平衡两个式子并没能够满足凸优化的要求。因此,将潮流方程改写成以下式子:
pi=∑k:j→kPjk−∑i:i→j(Pij−rijlij)∀j∈Nqi=∑k:j→kQjk−∑i:i→j(Qij−xijlij)∀j∈Nlij=Pij2+Qij2vi∀(i,j)∈ϵvj=vi−2(rijPij+xijQij)+(rij2+xij2)lij\begin{align} & p_i = \sum_{k:j\rightarrow k}P_{jk}-\sum_{i:i\rightarrow j}(P_{ij}-r_{ij}l_{ij})\quad \forall j\in N \\ & q_i = \sum_{k:j\rightarrow k}Q_{jk}-\sum_{i:i\rightarrow j}(Q_{ij}-x_{ij}l_{ij})\quad \forall j\in N\\ & l_{ij}=\frac{P_{ij}^2+Q_{ij}^2}{v_i} \quad \forall (i,j)\in \epsilon \\ & v_j = v_i - 2(r_{ij}P_{ij}+x_{ij}Q_{ij})+(r_{ij}^2+x_{ij}^2)l_{ij} \end{align} pi=k:j→k∑Pjk−i:i→j∑(Pij−rijlij)∀j∈Nqi=k:j→k∑Qjk−i:i→j∑(Qij−xijlij)∀j∈Nlij=viPij2+Qij2∀(i,j)∈ϵvj=vi−2(rijPij+xijQij)+(rij2+xij2)lij
其中,lij=∣Iij∣2l_{ij}=|I_{ij}|^2lij=∣Iij∣2, vi=∣Vi∣2v_i=|V_i|^2vi=∣Vi∣2
消除了{si}\{s_{i}\}{si}这个非线性项;
{Sij}\{S_{ij}\}{Sij}这一项也通过以上的lij=Pij2+Qij2vil_{ij}=\frac{P_{ij}^2+Q_{ij}^2}{v_i}lij=viPij2+Qij2式子解出,但由于这个等式约束非线性,一般进一步松弛,得到以下式子:
lij≥Pij2+Qij2vil_{ij}\geq\frac{P_{ij}^2+Q_{ij}^2}{v_i} lij≥viPij2+Qij2
从而去掉二次项,得到二阶锥约束。
考虑的问题
考虑两次松弛,面临松弛以后的解是否还是原问题的解的问题。此时,有结论:如网络是放射状网络,则能保证还是原问题的解;如是环状网络,则无法保证。
