多元组优先队列

C++ 多元组优先队列详解

定义与核心价值

多元组优先队列是一种特殊的优先队列，其元素为包含多个字段的复合结构（如二元组、三元组等），通过自定义多维度比较规则实现元素的有序管理。

核心价值：解决需要综合多个条件（维度）决定优先级的场景，例如：

• 任务调度：(优先级, 截止时间, 任务ID)
• 路径规划：(总距离, 时间开销, 节点ID)

实现方式对比

实现方式	适用场景	优点	缺点
自定义struct+重载operator<	多元组字段多、逻辑复杂	可读性强，字段访问直观	需额外定义结构体
std::tuple+自定义比较器	简单多元组（2-3个字段）	无需自定义结构体，简洁	字段访问依赖索引，可读性较差

实现方法详解

方法1：自定义struct+重载operator<

步骤思维导图

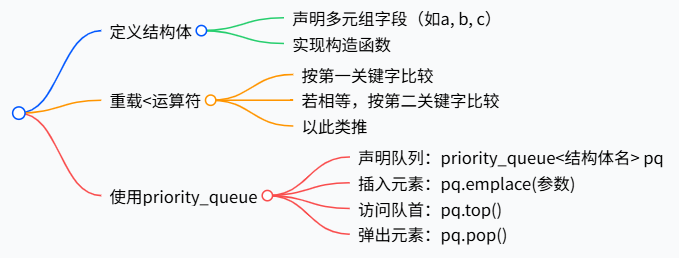
- 定义结构体
- 声明多元组字段（如a, b, c）
- 实现构造函数
- 重载<运算符
- 按第一关键字比较
- 若相等，按第二关键字比较
- 以此类推
- 使用priority_queue
- 声明队列：priority_queue<结构体名> pq
- 插入元素：pq.emplace(参数)
- 访问队首：pq.top()
- 弹出元素：pq.pop()

代码示例（二元组排序）

需求：优先按a降序，a相等则按b升序

#include <queue>
#include <iostream>
using namespace std;struct Tuple {int a;  // 第一关键字int b;  // 第二关键字// 构造函数Tuple(int a_, int b_) : a(a_), b(b_) {}// 重载<运算符bool operator<(const Tuple& other) const {if (a != other.a) {// a越大优先级越高：当前a < other.a时，other优先级更高return a < other.a;  } else {// b越小优先级越高：当前b > other.b时，other优先级更高return b > other.b;  }}
};int main() {priority_queue<Tuple> pq;pq.emplace(3, 2);pq.emplace(5, 1);pq.emplace(5, 0);while (!pq.empty()) {auto top = pq.top();pq.pop();cout << "a=" << top.a << ", b=" << top.b << endl;}return 0;
}

输出结果：

a=5, b=0
a=5, b=1
a=3, b=2

方法2：std::tuple+自定义比较器

步骤思维导图

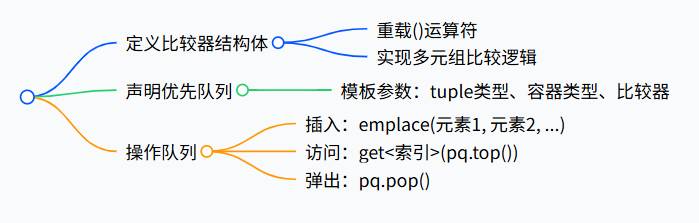
- 定义比较器结构体
- 重载()运算符
- 实现多元组比较逻辑
- 声明优先队列
- 模板参数：tuple类型、容器类型、比较器
- 操作队列
- 插入：emplace(元素1, 元素2, ...)
- 访问：get<索引>(pq.top())
- 弹出：pq.pop()

代码示例（三元组排序）

需求：按x升序→y降序→z升序

#include <queue>
#include <tuple>
#include <iostream>
using namespace std;// 自定义比较器
struct Compare {bool operator()(const tuple<int, int, int>& t1, const tuple<int, int, int>& t2) const {int x1 = get<0>(t1), y1 = get<1>(t1), z1 = get<2>(t1);int x2 = get<0>(t2), y2 = get<1>(t2), z2 = get<2>(t2);if (x1 != x2) return x1 > x2;  // x升序if (y1 != y2) return y1 < y2;  // y降序return z1 > z2;                // z升序}
};int main() {// 声明三元组优先队列priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, Compare> pq;pq.emplace(2, 5, 3);pq.emplace(1, 8, 1);pq.emplace(1, 9, 2);while (!pq.empty()) {auto [x, y, z] = pq.top();  // C++17结构化绑定pq.pop();cout << "x=" << x << ", y=" << y << ", z=" << z << endl;}return 0;
}

输出结果：

x=1, y=9, z=2
x=1, y=8, z=1
x=2, y=5, z=3

优先级比较逻辑解析

优先队列的核心是比较器的逻辑设计，对于两个多元组$T1=(f_1,f_2,...,f_n)$和$T2=(g_1,g_2,...,g_n)$：

1. 从第一个字段开始比较：若$f_1$和$g_1$的优先级可区分，则直接返回结果
2. 若$f_1=g_1$，则比较第二个字段$f_2$和$g_2$
3. 以此类推，直到找到可区分优先级的字段

数学描述：
$$T1\text{ 优先级高于 }T2⟺\exists k,\forall i<k:f_i=g_i\text{ 且 }{f}_k\text{ 优先级高于 }{g}_k$$

复杂度分析

操作	时间复杂度	说明
插入元素	$O(\log n)$	n为队列元素数，比较操作增加常数项
弹出元素	$O(\log n)$	同上
访问队首	$O(1)$	直接返回堆顶元素

空间复杂度：$O(n)$，需存储所有元素

典型应用场景

场景	多元组设计	比较规则
任务调度	(优先级, 截止时间, 任务ID)	优先级降序→截止时间升序
切割木棍问题	(长度, 数量)	长度降序（优先切割最长木棍）
Dijkstra算法扩展	(总距离, 时间, 节点)	总距离升序→时间升序
数据流Top-K	(指标1, 指标2, 数据)	指标1降序→指标2降序

注意事项

1. 比较器逻辑：priority_queue默认是大根堆，比较器返回true表示左侧元素优先级低于右侧
2. 字段访问：

• 自定义struct：直接通过成员变量访问（如top.a）
• std::tuple：通过get<索引>(tuple)访问（索引从0开始）

3. C++版本兼容：

• 结构化绑定（auto [x,y,z]）需C++17及以上
• 自定义比较器在C++11及以上支持

通过合理设计多元组结构和比较规则，可高效解决各类多维度优先级问题，是C++中处理复杂排序场景的重要工具。