LabVIEW实现B样条曲线拟合

​在 LabVIEW 中利用相关 VI 进行 B 样条曲线拟合，涵盖 1D、2D 等不同维度及多种曲线类型的拟合操作。

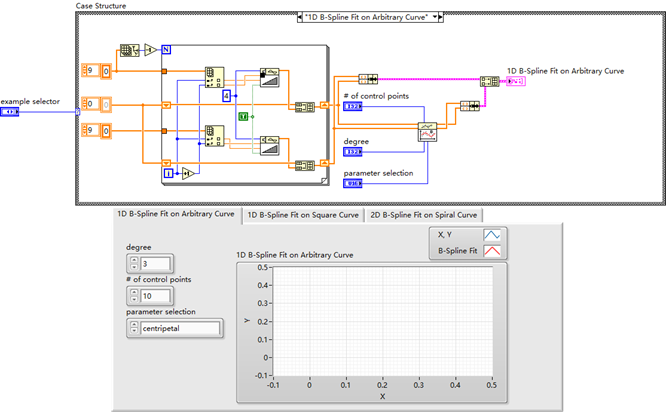
概念说明

B 样条（B - Spline）是一种用于曲线和曲面建模的数学工具，通过控制顶点和节点向量来定义平滑曲线，能灵活地表示复杂形状，在计算机辅助设计、计算机图形学等领域广泛应用。

VI 说明

• Ramp Pattern.vi

• • 功能：生成斜坡（线性变化）模式的数据。

  • 使用场合：在需要产生线性递增或递减数据序列的场景，如模拟信号的线性变化、为曲线拟合提供基础的线性数据等。

  • 特点：操作简单，能快速生成规则的线性数据模式。

  • 使用注意事项：需注意输入参数的范围和步长设置，避免数据溢出或不符合预期的线性变化。

  • 类似功能对比：与 “Sine Pattern.vi”（生成正弦模式数据）相比，“Ramp Pattern.vi” 生成线性数据，更适合线性相关的场景，而 “Sine Pattern.vi” 适用于周期性正弦信号相关的应用。

• B - Spline Fit.vi

• • 功能：实现 B 样条曲线拟合，根据输入的控制点、次数等参数，对数据进行 B 样条曲线的拟合计算。

  • 使用场合：用于对各类曲线（如任意曲线、方形曲线、螺旋曲线等）进行平滑拟合，在需要用 B 样条表示曲线形状的工程设计、图形绘制等领域。

  • 特点：支持 1D 和 2D 的 B 样条拟合，可通过设置次数、控制点数量、参数选择等灵活调整拟合效果，能较好地保持曲线的平滑性和灵活性。

  • 使用注意事项：次数设置过高可能导致计算复杂、曲线过度拟合；控制点数量需根据曲线复杂程度合理选择；参数选择（如 “centripetal”）要与数据特性匹配。

  • 类似功能对比：与 “Polynomial Fit.vi”（多项式拟合）相比，B 样条拟合更适合表示复杂的、非多项式的平滑曲线，多项式拟合在处理多项式形式的曲线时计算更简洁，但灵活性不如 B 样条拟合。

背景补充

B 样条因在曲线表示上的良好特性，成为计算机辅助几何设计的重要工具。LabVIEW 作为图形化编程环境，通过这些 VI 将 B 样条拟合的复杂数学计算封装起来，方便快速实现曲线拟合功能，提升了工程设计与图形处理等工作的效率。