算法基础篇(5)前缀和
前缀和与差分的核心思想是预处理,可以在暴力枚举的过程中,快速给出查询结果,从而优化时间复杂度。是经典的空间换时间的做法。
1、一维前缀和
1.1 【模板】前缀和

算法思路:
思路一:根据之前学的模拟算法暴力求解,但是这样的话时间复杂度为O(n * q),而n和q的值在10^5之间,所以时间复杂度过高,程序会存在超时的风险。
思路二:题目要求快速频繁地求出数组中某一段区间的和,这种情况下用前缀和算法是更优的。
先预处理出来一个前缀和数组f[i],f[i]表示区间[1,i]中所有元素的和,那么就可以得到递推公式:f[i] = f[i - 1] + a[i]。那为什么不用for循环来遍历得到f[i]中的值呢?这样会导致时间复杂度变为O(n^2)。那么如何利用前缀和数组呢?假如此时要计算区间[L,r]之间的和,只需要用f[r] - f[L - 1]即可。
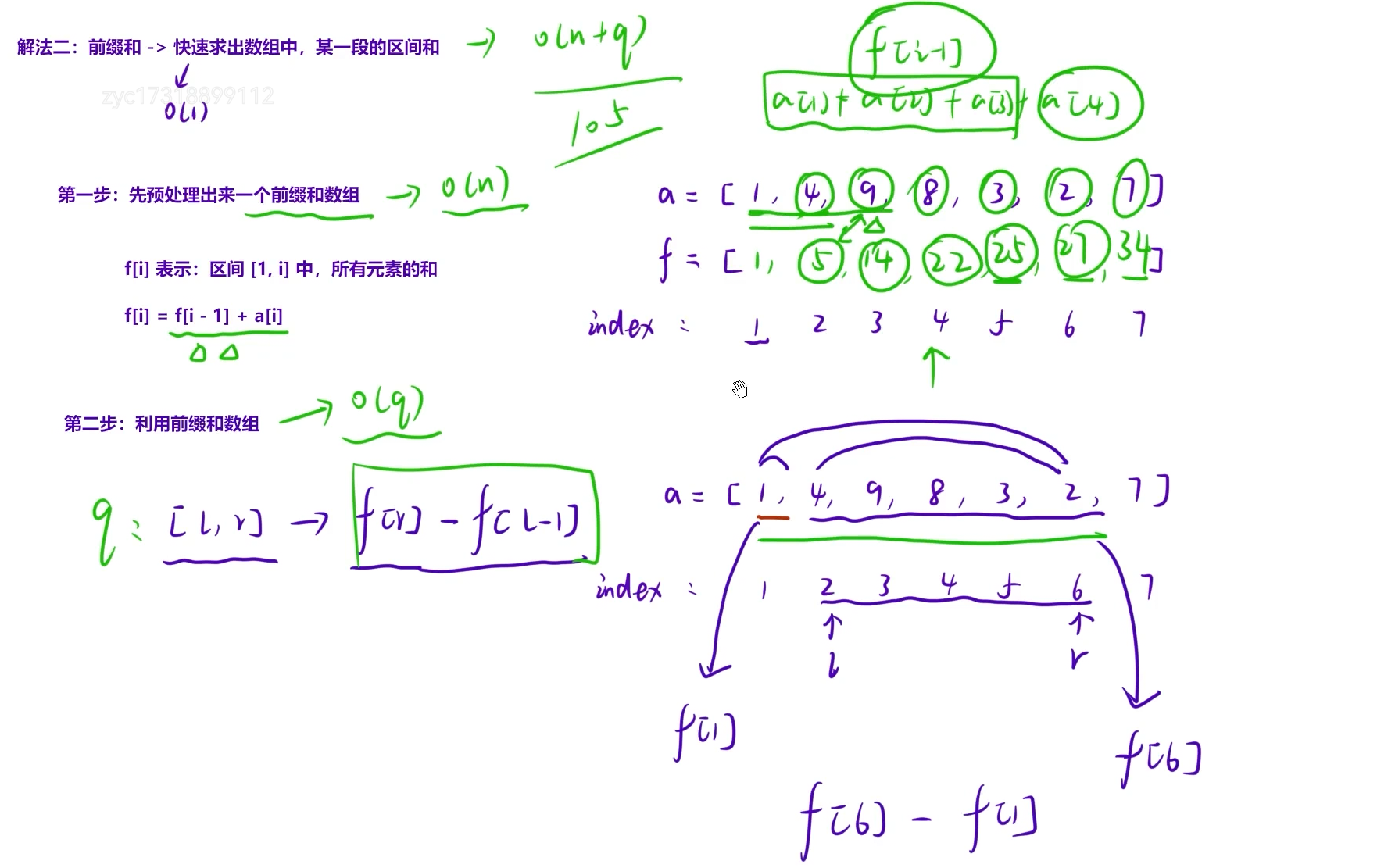
注意:使用前缀和数组时,下标必须从1开始计数。
参考代码:
#include <iostream>
using namespace std;const int N = 1e5 + 10;
int n, q;long long a[N];
long long f[N]; //前缀和数组int main()
{cin >> n >> q;for(int i = 1;i <= n;i++){cin >> a[i];}//处理前缀和数组for(int i = 1;i <= n;i++){f[i] = f[i - 1] + a[i];}//处理q次询问while(q--){int l, r;cin >> l >> r;cout << f[r] - f[l - 1] << endl;}return 0;
}1.2 【经典】最大子段和
算法思路:利用前缀和
在解决这道题之前,先思考一个问题:怎么求以a[i]为结尾的所有区间中最大的子段和呢?用f[i]减去前面区间的和,也就是f[i] - f[x],其中1 <= x <= i - 1。想要让该式子的值最大,也就是让减数f[x]最小就可以了。所以,这道题就是用f[i]减去[1,i-1]中所有前缀和的最小值即可。
参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;const int N = 2e5 + 10;int n;
long long f[N]; //前缀和数组int main()
{cin >> n;for (int i = 1;i <= n;i++){long long x;cin >> x;f[i] = f[i - 1] + x;}long long ret = -1e20;long long prevmin = 0;for (int i = 1;i <= n;i++){ret = max(ret, f[i] - prevmin);prevmin = min(prevmin, f[i]);}cout << ret << endl;return 0;
}2、二维前缀和
2.1 【模板】二维前缀和

算法思路:二维前缀和->快速查询二维数组中,某一个子矩阵中所有元素的和
第一步:预处理出来二维前缀和矩阵f[i][j],表示从[1,1]到[i,j]区域内,所有元素的和。
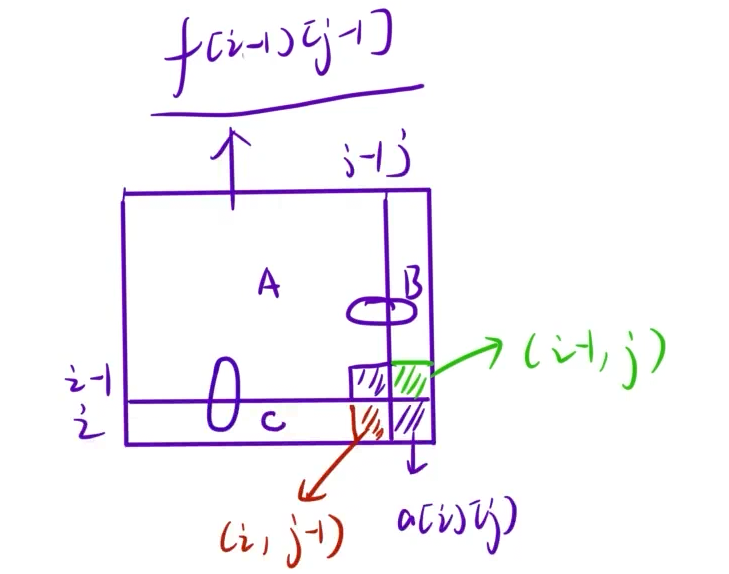
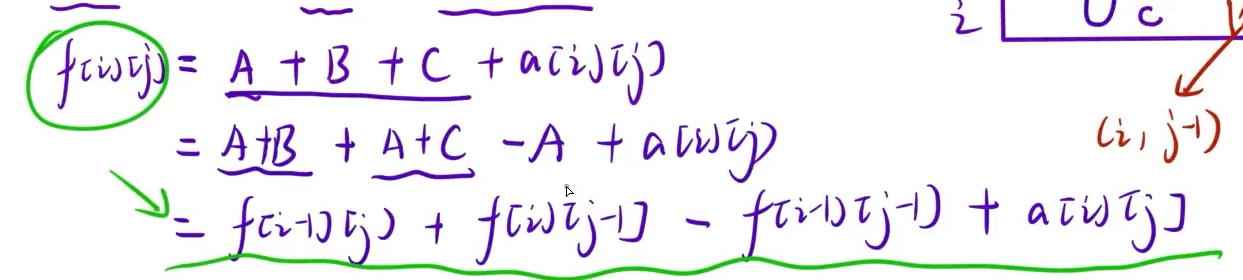
第二步:用前缀和矩阵解决问题。
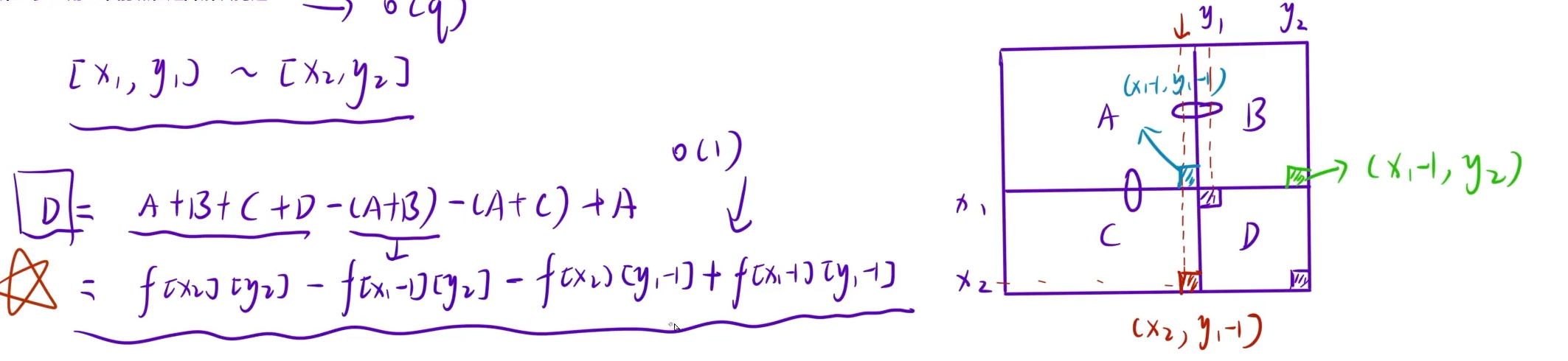
参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;const int N = 1010;int f[N][N];
int n, m, q;int main()
{cin >> n >> m >> q;//预处理前缀和矩阵for (int i = 1;i <= n;i++){for (int j = 1;j <= m;j++){int x;cin >> x;f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + x;}}//处理q次查询while (q--){int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1] << endl;}return 0;
}2.2 激光炸弹
题目描述

算法思路:在坐标系中枚举出所有边长为m的正方形,找出正方形中目标价值最大的即可。

参考代码:
#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
using namespace std;const int N = 1e4 + 10;int n, m;
int a[N][N];
int f[N][N]; //前缀和矩阵int main()
{cin >> n >> m;while (n--){int x, y, v;cin >> x >> y >> v;//下标从1开始计数x++; y++; a[x][y] += v; //同一个位置可能有多个目标}n = 5001;//预处理前缀和矩阵for (int i = 1;i <= n;i++){for (int j = 1;j <= n;j++){f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];}}int ret = 0;m = min(m, n); //如果 m 很大,相当于就是把整个区域全部摧毁//枚举所有边长为 m 的正方形for (int x2 = m;x2 <= n;x2++){for (int y2 = m;y2 <= n;y2++){int x1 = x2 - m + 1;int y1 = y2 - m + 1;ret = max(ret, f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1]);}}cout << ret << endl;return 0;
}