当前位置：首页 > news >正文

[数据结构]ST表（markdown重制版）

news 2025/9/26 13:00:05

								ST表

一、适用情况

ST 表能在 $O (1)$ 的时间内查询满足可重复贡献问题(幂等性)和结合律的区间信息

如:区间最值,区间GCD,区间LCM,区间按位或,区间按位与等

st[i][j] 表示起点为i ，区间长度为 $2^j$ 的gcd或者max等

也就是a[i,i+(1<<j)-1]内的gcd

二、如何递推?

首先要初始化
遍历每个i 将st[i][0]赋值成a[i] ，因为j==0表示区间长度为 $2^0$ 即为1
也就是起点所对应的元素本身

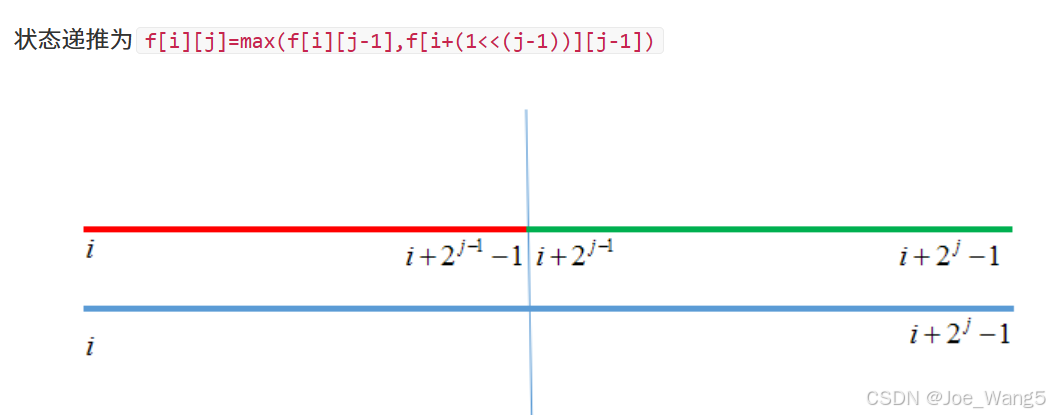
下标示意图
在两个相邻的区间内取max或gcd 这两个区间的起点相邻区间长度相同
都是 $2^{j-1}$ 区间合并刚好就是要求的区间

三、如何查询？

`query(L, R)` 的具体步骤：

计算区间的长度：
首先，计算区间的长度：
len = R - L + 1
找到最大可以覆盖该区间长度的 $2^k$ ：
对于给定区间的长度，我们需要找到一个最大的 k，使得 2^k 小于等于该长度 len。
这个 k 可以通过 $log_2(len)$ 来计算，因为 $log_2(len)$ 给出的是最大的 k，使得 $2k≤len2^k \le len$ ， $log_2(len)$ 用int接收后面的小数就被截断
所以一个 $2^k$ 无法完全覆盖len，所以将目标区间拆成两个部分（有重叠）
将区间 [L, R] 分为两个子区间：
通过选定的 k 值，区间 [L, R] 被分成两部分：
计算int k=log(r-l+1);

第一个子区间：从 L 到 L + 2^k - 1（即，长度为 2^k）
第二个子区间：从 R - 2^k + 1 到 R（也是长度为 2^k）

子区间重叠对于max, gcd 等操作毫无影响，这就是st表巧妙的一点
通过k 将[l,r]分成两个可能有重叠的子区间重叠并不会造成影响

四、代码实现

1. 模板

#include <iostream>
#include <cmath>
using namespace std;const int MAX_N = 1000;  // 假设最大元素个数为1000
const int MAX_LOG = 10;   // 假设 n 最多为 2^10 = 1024int arr[MAX_N];   // 存储原始数组
int st[MAX_N][MAX_LOG];  // ST表，st[i][j] 表示区间 [i, i + 2^j - 1] 的最小值
// 构建 ST 表
void build(int n) {for (int i = 0; i < n; i++) {st[i][0] = arr[i];}for (int j = 1; (1 << j) <= n; j++)for (int i = 0; i + (1 << j) - 1 < n; i++)st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}int query(int L, int R) {int len = R - L + 1;int k = __lg(len);return min(st[L][k], st[R - (1 << k) + 1][k]);
}int main() {int n;cin >> n;for (int i = 0; i < n; i++) cin >> arr[i];build(n);int L, R;cin >> L >> R;cout << "区间 [" << L << ", " << R << "] 的最小值为: " << query(L, R) << endl;
}

1.__lg()取以2为底的对数向下取整即 n 在二进制中的最高位 1 的位置（从 0 开始计数）时间复杂度 $O (1)$

2.build中 外层循环先遍历第二维j 就是按区间长度从小到大遍历 (1<<j)<=n

内层循环遍历起点i 循环结束条件是区间终点不越界也就是i+(1<<j)-1<n 要记得区间终点-1 计算起点+1

2. Codeforces Round 991 (Div. 3)F题

const int N = 2e5 + 10;
int a[N], n, q, st[N][20];
// 最大的log(n)，最大n=2e5所以log(2e5)大约为 18，取 20 以保证覆盖范围
void build() {for (int i = 0; i < n - 1; i++) st[i][0] = abs(a[i] - a[i + 1]);for (int j = 1; (1 << j) <= n; j++)for (int i = 0; i + (1 << j) - 1 < n - 1; i++)st[i][j] = gcd(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
int query(int l, int r) {int k = __lg(r - l + 1);return gcd(st[l][k], st[r - (1 << k) + 1][k]);
}
void solve() {cin >> n >> q;for (int i = 0; i < n; i++) cin >> a[i];// memset(st,1,sizeof st);for (int i = 0; i < n - 1; i++)for (int j = 0; j < 20; j++) st[i][j] = 1;build();while (q--) {int l, r;cin >> l >> r;if (l == r) {cout << 0 << ' ';continue;}l--, r -= 2;cout << query(l, r) << ' ';}cout << endl;
}