软件设计师——02 程序设计语言基础知识
1 程序设计语言概述
1.1 程序设计语言的基本概念
-
程序设计语言是人为设计的符号语言,用于书写计算机程序,描述、组织和推导计算过程;
-
分类:
- 低级语言:包括机器语言(由0、1序列构成,是计算机能直接识别的语言)和汇编语言(用助记符代替机器指令的操作码和地址码,更易被程序员理解,但仍依赖硬件);
- 高级语言:功能更强,抽象级别更高,和人们使用的自然语言更接近,方便程序员编写程序;
-
各程序设计语言的特点:
- Fortran语言:适用于科学计算,执行效率高,在科学计算领域应用广泛;
- Pascal语言:为教学而开发,表达能力强,有助于初学者学习程序设计的基本概念和方法;
- C语言:指针操作能力强,且运行高效,既能用于底层系统开发,也能用于应用程序开发;
- C++语言:具有面向对象的特性,同时保持了高效性,适合开发大型复杂的软件系统;
- Java语言:面向对象,通过生成中间代码(字节码)实现跨平台运行,可在不同操作系统上运行,在企业级应用、移动应用等领域大量使用;
- C#语言:面向对象,使用中间代码,依托.NET框架,在Windows平台的应用开发中较为常用;
- Python语言:面向对象,属于脚本语言和解释型语言(程序运行时逐行解释执行),语法简洁,在数据分析、人工智能、Web开发等众多领域都有广泛应用;
- JavaScript语言:是脚本语言,广泛用于Web开发,可实现网页的交互功能,如表单验证、动态内容展示等。
-
练习:Python中采用()原方法来获取一个对象的类型。
- A.str()
- B.type()
- C.id()
- D.object()
B
在Python中,
type()函数返回对象的类型,能够帮助我们确定对象所属的类(class),例如:str()方法是将对象转换为字符串的方法,id()方法返回对象的唯一标识符,object()是 Python 的内置函数之一,它返回一个新的object对象。这个对象没有任何特殊的属性或方法,它是所有类的基类,即所有 Python 类都直接或间接地继承自object类。答案选B。 -
练习:在Python语言中,语句x =()不能定义一个元组。
- A.(1, 2, 1, 2)
- B.1, 2, 1, 2
- C.tuple()
- D.(1)
D
对于选项D,由于括号()既可以用来表示数学中的一个表达式,也可以用来括起元组,因此(1)并不表示一个元组,它实际上等价于整数1。如果想要定义只有一个元素的元组,需要在元素后面加上逗号来消除歧义,例如(1,)表示只包含一个元素的元组。
1.2 程序设计语言的基本成分
-
数据成分:
- 指一种程序设计语言的数据与数据类型;
- 数据分为常量(程序运行时不可改变)、变量(程序运行时可改变)、全局量(存储空间在静态数据区分配)、局部量(存储空间在堆栈区分配);
- 数据类型有整型、字符型、单精度浮点型、双精度浮点型、布尔型、枚举类型等;
-
运算成分:
- 规定了允许使用的运算符及运算规则;
- 包含算术运算、逻辑运算、关系运算、位运算等;
-
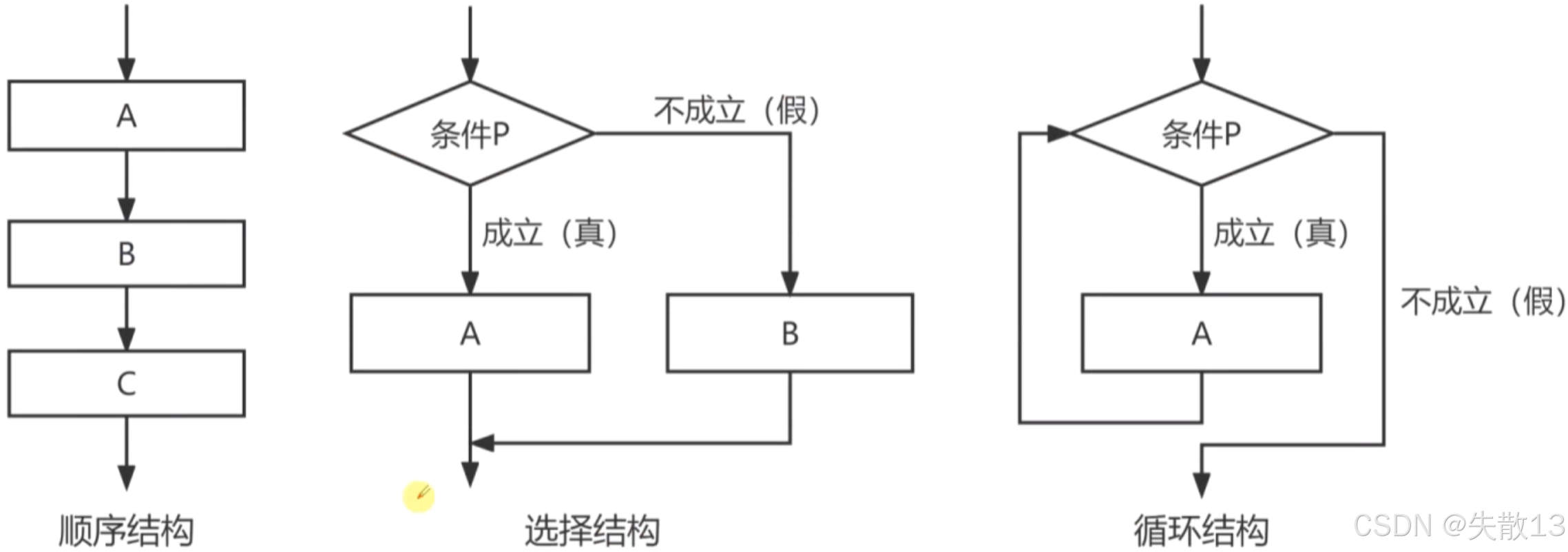
控制成分:指明语言允许表述的控制结构,有顺序结构、选择结构、循环结构(包含初始化、循环体、循环终止条件);
- 顺序结构是代码按顺序依次执行;
- 选择结构根据条件判断,选择执行不同的代码分支;
- 循环结构在条件成立时,重复执行某段代码;
-
传输成分:明确语言允许的数据传输方式,像赋值处理、数据的输入输出等;
-
函数:
-
函数是一段具有独立处理功能的代码块,其使用涉及函数定义、函数声明(先声明再使用)、函数调用三个概念。
-
函数定义:用于实现具体的功能逻辑,格式如下:
返回值类型 函数名(形参…) // 函数首部 {函数体; } -
函数声明:主要是提前告知编译器函数的相关信息,格式如下:
返回值类型 函数名(参数类型…) // 函数声明 -
函数调用:用于执行函数定义好的功能,格式如下:
函数名(实参…); // 函数调用
-
-
函数调用的两种方式:
- 传值调用:把实参的值传递给形参,形参的改变不会使实参发生改变,实参可以是合法的变量、常量或表达式;
- 引用调用(传地址调用):将实参的地址传递给形参,相当于对实参存储单元进行地址引用,所以形参的值改变时,实参的值也会跟着改变,实参不能为常量,只能是合法的变量和表达式;
-
-
练习:通用的高级程序设计语言一般都会提供描述数据、运算、控制和数据传输的语言成分,其中,控制包括顺序、()和循环结构。
- A.选择
- B.递归
- C.递推
- D.函数
A
-
设函数foo和hoo的定义如下所示,在函数foo中调用函数hoo,hoo的第一个参数采用传引用方式(call by reerence),第二个参数采用传值方式(call by value),那么函数foo中的print(a, b)将输出()。
foo() int a = 8, b = 5; hoo(a, b); print(a, b);hoo (int &x, int m) m = x * m; x = m - 1; return;- A.8, 5
- B.39, 5
- C.8, 40
- D.39, 40
B
foo函数中调用hoo函数时传入的第一个参数为变量a,在函数hoo中通过引用传递方式修改了a的值(x=40-1→a=40-1→a=39),因此当foo函数中print(a, b)被调用时,a的值已经被修改为39。而传入hoo函数的第二个参数是变量b,它采用的是传值方式,因此在hoo函数中对b的修改不会影响到foo中b的值。因此,print(a, b)将输出:39, 5,答案选B。
2 语言处理程序基础
2.1 汇编程序基本原理
- 汇编语言是为特定的计算机或计算机系统设计的,是面向机器的符号化的程序设计语言;
- 汇编程序的作用是将汇编语言所编写的源程序翻译成机器指令程序。汇编程序一般需要两次扫描源程序才能完成翻译过程;
- 第一次扫描:主要进行两项工作,一是检查语法错误,二是确定符号名字并建立符号表;
- 第二次扫描:产生目标程序,也就是将汇编语言源程序转换为机器能够直接识别和执行的机器指令程序。
2.2 编译程序基本原理
2.2.1 编译程序概述
-
编译程序的功能是把某高级语言书写的源程序翻译成与之等价的目标程序(汇编语言或机器语言)。其工作过程分为6个阶段:
-
词法分析:从左到右逐个字符扫描源程序,识别出一个个**“单词”符号**;
比如:有这么一行代码:
int a = 1;,词法分析就是识别出int、a、=、1、;这一个个“单词”符号; -
语法分析:在词法分析基础上,将单词序列组合成各类语法短语(如“程序”“语句”“表达式”等),判断源程序在结构上是否正确;
-
语义分析:对结构正确的源程序进行上下文有关性质审查和类型审查(如类型匹配、除数不为0等)。分为静态语义错误(编译阶段可查)和动态语义错误(运行时才能发现);
-
中间代码生成(非必须):根据语义分析产生中间代码,需经优化链接生成可执行目标代码。引入中间代码是为进行与机器无关的代码优化,提升可移植性。常用中间代码有后缀式(逆波兰式)、三元式(三地址码)、四元式、树和图等形式;
-
代码优化(非必须):若要生成高效目标代码,就依据程序的等价变换原则进行优化;
-
目标代码生成:把中间代码变换成特定机器上的绝对指令代码、可重定位的指令代码或汇编指令代码。该阶段工作与具体机器密切相关,需考虑三个问题:如何生成较短的目标代码;如何充分利用计算机中的寄存器,减少目标代码访问存储单元的次数;如何充分利用计算机指令系统的特点,以提高目标代码的质量;

-
-
练习:在对高级语言源程序进行编译或解释处理的过程中,需要不断收集、记录和使用源程序中一些相关符号类型和特征等信息,并将其存入()中。
- A.哈希表
- B.符号表
- C.堆栈
- D.队列
B
符号表的作用是记录源程序中各个符号的必要信息,以辅助语义的正确性检查和代码生成,在编译过程中需要对符号表进行快速有效地查找、插入、修改和删除等操作。符号表的建立可以始于词法分析阶段,也可以放到语法分析和语义分析阶段,但符号表的使用有时会延续到目标代码的运行阶段。
-
练习:对高级程序语言进行编译的过程中,使用()来记录源程序中各个字符的必要信息,以辅助语义的正确性检查和代码生成。
- A.决策表
- B.符号表
- C.广义表
- D.索引表
B
符号表的作用是记录源程序中各个符号的必要信息,以辅助语义的正确性检查和代码生成,在编译过程中需要对符号表进行快速有效地查找、插入、修改和删除等操作。符号表的建立可以始于词法分析阶段,也可以放到语法分析和语义分析阶段,但符号表的使用有时会延续到目标代码的运行阶段。
-
练习:以编译方式翻译C/C++源程序的过程中,类型检查在()阶段处理。
- A.词法分析
- B.语义分析
- C.语法分析
- D.目标代码生成
B
语义分析:语义分析的任务是对结构上正确的源程序进行上下文有关性质的审查和类型审查。如类型匹配、除数不为0等。又分为静态语义错误(在编译阶段能够查找出来)和动态语义错误(只能在运行时发现)。语义分析的一个主要工作是进行类型分析和检查。
-
练习:将编译器的工作过程划分为词法分析,语法分析,语义分析,中间代码生成,代码优化和目标代码生成时,语法分析阶段的输入是()。若程序中的括号不配对,则会在()阶段检查出错误。
- A.记号流
- B.字符流
- C.源程序
- D.分析树
- A.词法分析
- B.语法分析
- C.语义分析
- D.目标代码生成
A B
词法分析阶段的任务是对源程序从前到后(从左到右)逐个字符地扫描,从中识别出一个个“单词”符号,称为记号。在词法分析的基础上,语法分析的任务是根据语言的语法规则将记号(单词符号)序列分解成各类语法单位,如“表达式”“语句”等。语法分析阶段分析语法结构的含义,检查源程序是否包含静态语义错误,并收集类型信息供后面的代码生成阶段使用。只有语法和语义都正确的源程序才能翻译成正确的目标代码。括号不匹配属于语法错误,在语法分析阶段可以发现该错误。
-
练习:以编译方式翻译C/C++源程序的过程中,()阶段的主要任务是对各条语句的结构进行合法性分析。
- A.词法分析
- B.语义分析
- C.语法分析
- D.目标代码生成
C
词法分析阶段是编译过程的第一个阶段,这个阶段的任务是对源程序从前到后(从左到右)逐个字符地扫描,从中识别出一个个“单词”符号。语法分析的任务是在词法分析的基础上,根据语言的语法规则将单词符号序列分解成各类语法单位,如“表达式”“语句”等。语法规则就是各类语法单位的构成规则。通过语法分析确定整个输入串是否构成一个语法上正确的程序。语义分析阶段分析各语法结构的含义,检查源程序是否包含静态语义错误,并收集类型信息供后面的代码生成阶段使用。只有语法和语义都正确的源程序才能翻译成正确的目标代码。
*中间代码生成的后缀式
-
给出一棵语法树,用中间代码来表示的话,有三种表达式形式:
- 前缀表达式:以
+ab为例,运算符在运算对象前面; - 中缀表达式:即常见的
a + b形式,是正常表达式的中序遍历形式; - 后缀表达式(逆波兰式):如
ab+,运算符在运算对象后面,由逻辑学家卢卡西维奇发明;
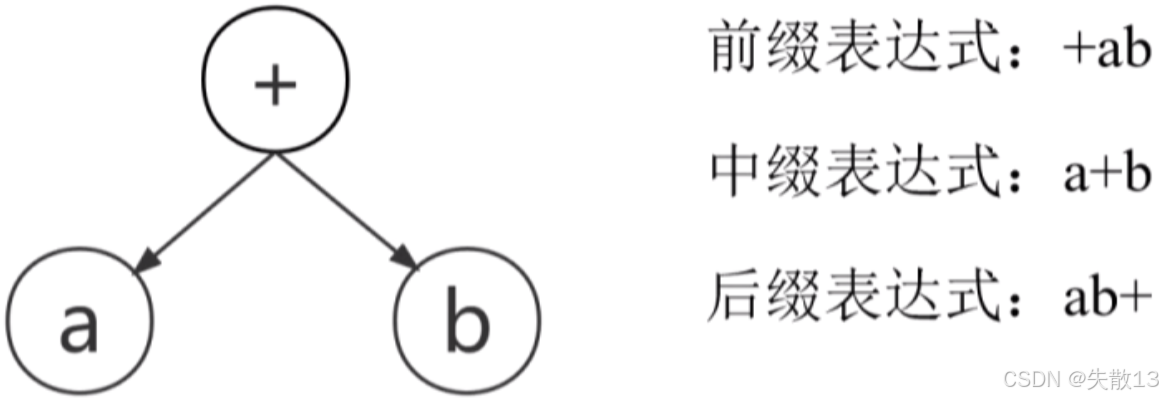
- 前缀表达式:以
-
这三种表达式其实对应树的三种遍历方式,正常表达式(中缀表达式)是中序遍历,可根据中缀表达式构造出一棵树,再据此求出前缀和后缀表达式;
-
后缀式的特点:把运算符号写在运算对象后面,比如
a + b写成ab+。优点是能根据运算对象和运算符的出现次序进行计算,不需要使用括号; -
后缀式的简单求法:按运算的优先顺序依次将运算符写在运算对象的后面,例如
a + b可写成ab+。 -
练习:

C
-
练习:

A
2.2.2 文法
-
文法的定义:描述语言语法结构的规则称为文法。一个形式文法是有序四元组G=(VN,VT,P,S)G=(V_N, V_T, P, S)G=(VN,VT,P,S),各部分含义如下:
- VNV_NVN:非终结符集合。非终结符不是语言的组成部分,也不是最终结果,可理解为“占位符”,能够推导出其他元素;
- VTV_TVT:终结符集合。终结符是语言的组成部分,是最终结果,且VN∩VT=∅V_N \cap V_T = \varnothingVN∩VT=∅(非终结符集合和终结符集合没有交集),终结符不能推导出其他元素;
- PPP:产生式集合。形式为α→β\alpha \to \betaα→β,表示用非终结符推导出终结符的规则,也就是非终结符推导出终结符的公式;
- SSS:起始符。是语言的开始符号;
-
正则闭包:对于集合$ A ,其正则闭包,其正则闭包,其正则闭包A^+ = A^1 \cup A^2 \cup A^3 \cup \cdots \cup A^n \cup \cdots,即所有幂(,即所有幂(,即所有幂(A的1次幂、2次幂、3次幂……的1次幂、2次幂、3次幂……的1次幂、2次幂、3次幂……n$次幂等)的组合;
-
闭包:闭包A∗=A0∪A+A^* = A^0 \cup A^+A∗=A0∪A+,是在正则闭包的基础上,加上A0={ε}A^0 = \{ \varepsilon \}A0={ε}($ \varepsilon $表示空串);
-
示例:
- 对于a∗a^*a∗,根据闭包定义,a∗={ε,a,aa,aaa,⋯ }a^* = \{ \varepsilon, a, aa, aaa, \cdots \}a∗={ε,a,aa,aaa,⋯}
- 对于(ab)∗(ab)^*(ab)∗,(ab)∗={ε,ab,abab,ababab,⋯ }(ab)^* = \{ \varepsilon, ab, abab, ababab, \cdots \}(ab)∗={ε,ab,abab,ababab,⋯}。
-
练习:已知文法G: S → A0|B1,A → S1|1,B → S0|0,其中S是开始符号。从S出发可以推导出()。
- A.所有由0构成的字符串
- B.所有由1构成的字符串
- C.某些0和1个数相等的字符串
- D.所有0和1个数不同的字符串
C
本题考查文法的推导式。将A和B代入S推导式,得到S → (S11)0|(S0|0)1 → S10|10|S01|01,此公式中只有S,没有其他符号,可以看出每个或符号包含的0和1的个数相等,因此从S出发推导出的文法中,0和1同时出现,所以他们的个数必然相等。
2.2.3 文法的分类
| 类型 | 别称 | 说明 | 对应自动机 |
|---|---|---|---|
| 0型 | 短语文法 | G的每条产生式α→β\alpha \to \betaα→β,满足α∈(VN∪VT)+\alpha \in (V_N \cup V_T)^+α∈(VN∪VT)+且至少含有一个非终结符,而β∈(VN∪VT)∗\beta \in (V_N \cup V_T)^*β∈(VN∪VT)∗ | 图灵机 |
| 1型 | 上下文有关文法 | G的任何产生式α→β\alpha \to \betaα→β(S→εS \to \varepsilonS→ε除外),均满足$ | \alpha |
| 2型 | 上下文无关文法 | G的任何产生式形如A→βA \to \betaA→β,AAA为非终结符,β∈(VN∪VT)∗\beta \in (V_N \cup V_T)^*β∈(VN∪VT)∗ | 非确定的下推自动机 |
| 3型 | 正规文法 | G的任何产生式形如A→aA \to aA→a或A→aBA \to aBA→aB(或者A→BaA \to BaA→Ba,aaa属于终结符,AAA、BBB属于非终结符) | 有限自动机 |
- 程序设计语言的绝大多数语法规则可以采用上下文无关文法进行描述。
2.2.4 正规表达式
-
正规表达式用于描述正规集,正规集是符合特定规则的字符串集合。以下是正规式及其表示的正规集的递归定义:
-
**$ \varepsilon (空串)∗∗:(空串)**:(空串)∗∗: \varepsilon 是一个正规式,它表示的正规集是一个正规式,它表示的正规集是一个正规式,它表示的正规集L(\varepsilon) = { \varepsilon }$,即该正规集仅包含空串这一个元素;
-
单个字符aaa:若aaa是Σ\SigmaΣ上的字符,那么aaa是一个正规式,它所表示的正规集为{a}\{ a \}{a},也就是该正规集只包含字符aaa这一个元素;
-
若正规式rrr和sss分别表示正规集L(r)L(r)L(r)和L(s)L(s)L(s),则:
-
选择(或)运算r∣sr|sr∣s:r∣sr|sr∣s是正规式,表示的正规集为L(r)∪L(s)L(r) \cup L(s)L(r)∪L(s),即由属于L(r)L(r)L(r)或者属于L(s)L(s)L(s)的所有字符串组成的集合;
-
连接运算r⋅sr \cdot sr⋅s:r⋅sr \cdot sr⋅s是正规式,表示的正规集为L(r)L(s)L(r)L(s)L(r)L(s),即由先取L(r)L(r)L(r)中的一个字符串,再取L(s)L(s)L(s)中的一个字符串,将它们连接起来形成的所有字符串组成的集合;
-
闭包(星闭包)运算r∗r^*r∗:r∗r^*r∗是正规式,表示的正规集为(L(r))∗(L(r))^*(L(r))∗,其中(L(r))∗(L(r))^*(L(r))∗是L(r)L(r)L(r)的闭包,包含空串$ \varepsilon 以及以及以及L®中字符串的一次或多次连接(即中字符串的一次或多次连接(即中字符串的一次或多次连接(即L®$中字符串的0次、1次、2次……连接);
-
括号运算(r)(r)(r):(r)(r)(r)是正规式,表示的正规集为L(r)L(r)L(r);
-
-
-
仅由有限次地使用上述三个步骤(基础情况的两个步骤以及组合情况的四个步骤)定义的表达式才是Σ\SigmaΣ上的正规式;
-
设Σ=a,b\Sigma={a,b}Σ=a,b,如下列出了Σ\SigmaΣ上的一些正规式和响应的正规集:
好的,这是修改后的表格,使用标准的 Markdown 公式语法
$来显示:正规式 正规集 举例 ababab 字符串 ababab 构成的集合 ab{ab}ab a∣ba|ba∣b 字符串 aaa、bbb 构成的集合 a,b{a, b}a,b a∗a^*a∗ 由0个或多个 aaa 构成的集合 ε,a,aa,aaa,…{\varepsilon, a, aa, aaa, \dots}ε,a,aa,aaa,… (a∣b)∗(a|b)^*(a∣b)∗ 所有字符串 aaa 和 bbb 构成的集合 ε,a,b,ab,ba,aab,bba,aba,…{\varepsilon, a, b, ab, ba, aab, bba, aba, \dots}ε,a,b,ab,ba,aab,bba,aba,… a(a∣b)∗a(a|b)^*a(a∣b)∗ 以 aaa 为首字符的 aaa、$ b $ 字符串的集合 a,aa,ab,aab,aba,abaa,aabab,…{a, aa, ab, aab, aba, abaa, aabab, \dots}a,aa,ab,aab,aba,abaa,aabab,… (a∣b)∗abb(a|b)^*abb(a∣b)∗abb 以 abbabbabb 结尾的 aaa、bbb 字符串的集合 abb,aabb,babbb,aaabbb,…{abb, aabb, babbb, aaabbb, \dots}abb,aabb,babbb,aaabbb,… -
练习:设有正规式s=(0∣10)∗s = (0|10)^*s=(0∣10)∗,则其所描述正规集中字符串的特点是()。
- A.长度必须是偶数
- B.长度必须是奇数
- C.0不能连续出现
- D.1不能连续出现
D
s=(0∣10)∗s = (0|10)^*s=(0∣10)∗表示的正规集为{ε,0,10,00,010,100,1010,000,0010,0100,01010,1000,10010,10100,101010,… }\{ \varepsilon, 0, 10, 00, 010, 100, 1010, 000, 0010, 0100, 01010, 1000, 10010, 10100, 101010, \dots \}{ε,0,10,00,010,100,1010,000,0010,0100,01010,1000,10010,10100,101010,…},用自然语言描述其正规式特点就是0可以连续出现,1不能连续出现,长度没有必须是奇数或偶数的特点。
2.2.5 有限自动机
2.2.5.1 确定的有限自动机(DFA)
-
定义:是词法分析的工具,一个确定的有限自动机DFA是一个五元组M=(S,Σ,f,S0,Z)M = (S, \Sigma, f, S_0, Z)M=(S,Σ,f,S0,Z),各部分含义如下:
- SSS:是一个有限集,其每个元素称为一个状态
- Σ\SigmaΣ:是一个有穷字母表,其每个元素称为一个输入字符
- fff:是状态转换函数,为S×ΣS \times \SigmaS×Σ上的单值部分映像。f(A,a)=Qf(A, a) = Qf(A,a)=Q表示当前状态为$ A 、输入为、输入为、输入为a时,将转换到下一个状态时,将转换到下一个状态时,将转换到下一个状态 Q ,称,称,称 Q 为为为 A $的一个后继状态
- S0∈SS_0 \in SS0∈S:是唯一的一个开始状态
- ZZZ:是非空的终止状态集合,其中Z⊆SZ \subseteq SZ⊆S
-
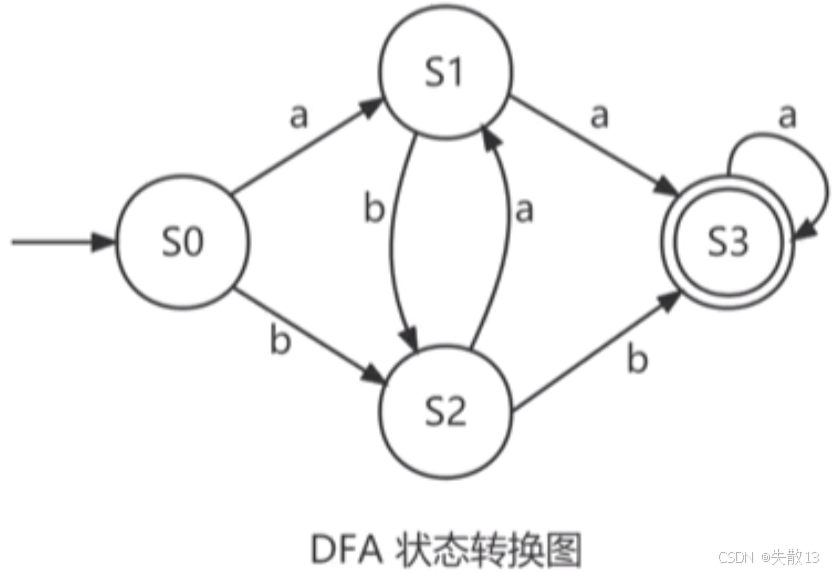
有限自动机可以形象地用状态转换图表示,设有限自动机:
DFA=({S0,S1,S2,S3},{a,b},f,S0,{S3}) DFA = (\{S_0, S_1, S_2, S_3\}, \{a, b\}, f, S_0, \{S_3\}) DFA=({S0,S1,S2,S3},{a,b},f,S0,{S3})-
其中状态转换函数fff为:f(S0,a)=S1f(S_0, a) = S_1f(S0,a)=S1,f(S0,b)=S2f(S_0, b) = S_2f(S0,b)=S2,f(S1,a)=S3f(S_1, a) = S_3f(S1,a)=S3,f(S1,b)=S2f(S_1, b) = S_2f(S1,b)=S2,f(S2,a)=S1f(S_2, a) = S_1f(S2,a)=S1,f(S2,b)=S3f(S_2, b) = S_3f(S2,b)=S3,f(S3,a)=S3f(S_3, a) = S_3f(S3,a)=S3;
-
从S0S_0S0输入一个aaa,可得出S1S_1S1;输入一个bbb,可得出S2S_2S2,以此类推;
-
-
一般的题目会给出一个状态转换图,判断能否构造出某字符串(如abbiabbiabbi),方法是看从起始状态(如S0S_0S0)到终止状态(如S3S_3S3)之间是否有一条路,权值为该字符串,本质就是有向图从起点到终点的遍历。
2.2.5.2 不确定的有限自动机(NFA)
- 定义:是词法分析的工具,一个不确定的有限自动机NFA是一个五元组M=(S,Σ,f,S0,Z)M = (S, \Sigma, f, S_0, Z)M=(S,Σ,f,S0,Z),各部分含义:
- SSS:是一个有限集,其每个元素称为一个状态
- Σ\SigmaΣ:是一个有穷字母表,其每个元素称为一个输入字符
- fff:是状态转换函数,为S×ΣS \times \SigmaS×Σ上的多值部分映像。f(A,a)=Qf(A, a) = Qf(A,a)=Q或$ f(A, a) = W 表示当前状态为表示当前状态为表示当前状态为 A 、输入为、输入为、输入为a时,将转换到下一个状态时,将转换到下一个状态时,将转换到下一个状态 Q 或或或 W $,即给定一个状态和输入符号,其后继状态可能有多个
- $ S_0 \in S $:是非空初态集
- ZZZ:是可空的终止状态集合
2.2.5.3 DFA与NFA的关系
-
DFA是NFA的特例:对于每一个NFA,都可以转换为DFA;
-
区分方法:输入一个字符,看是否能得出唯一的后继,若能,则是确定的有限自动机(DFA),否则就是不确定的有限自动机(NFA);
-
DFA 与 NFA 的区别:
区别 确定的有限自动机 不确定的有限自动机 初态 有且只有一个初态 可以有多个初态(非空) 终态 非空终态集 可空终态集 输入(弧上的标记) 输入仅能为长度为1的单个字符 输入可以是字符或正规式。同一个字符可以出现在同状态的多条弧上 后继状态 若有后继状态,则后继状态是唯一的 后继状态不是唯一的 其他 易于程序实现 易于人工设计 -
正规式与有限自动机之间的转换:
-
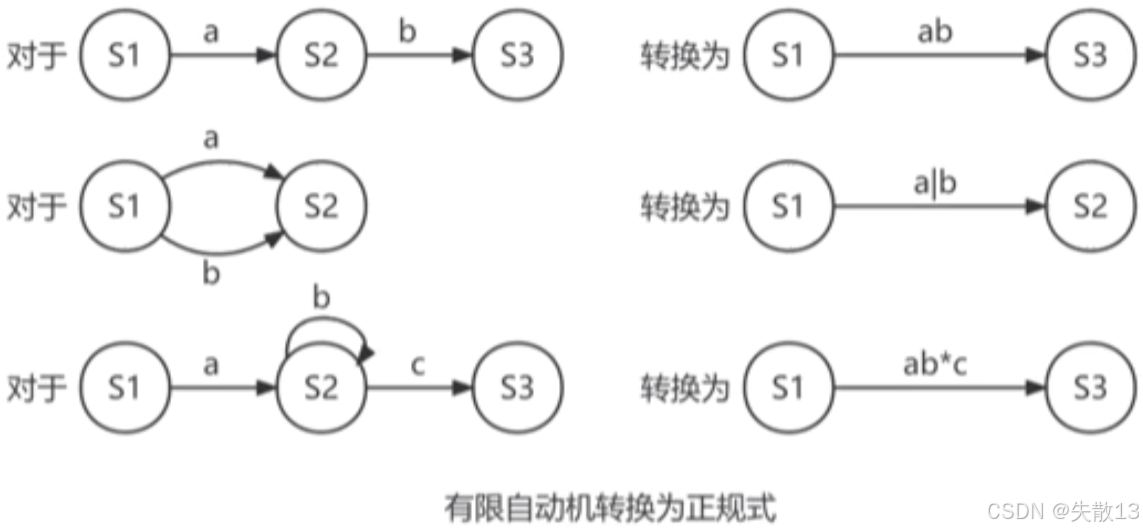
有限自动机转换为正规式的过程:
-
正规式转换为有限自动机的过程:
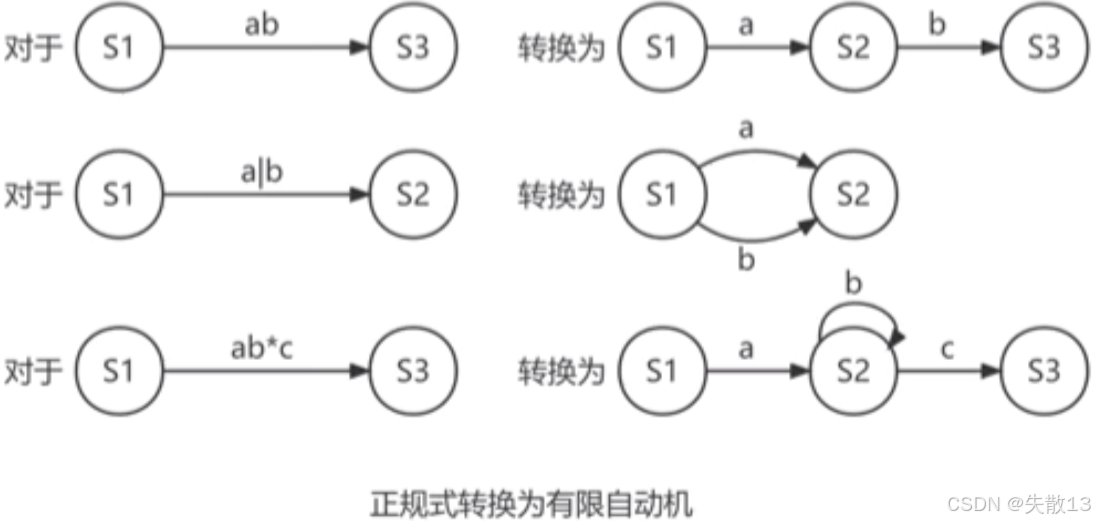
-
-
练习:
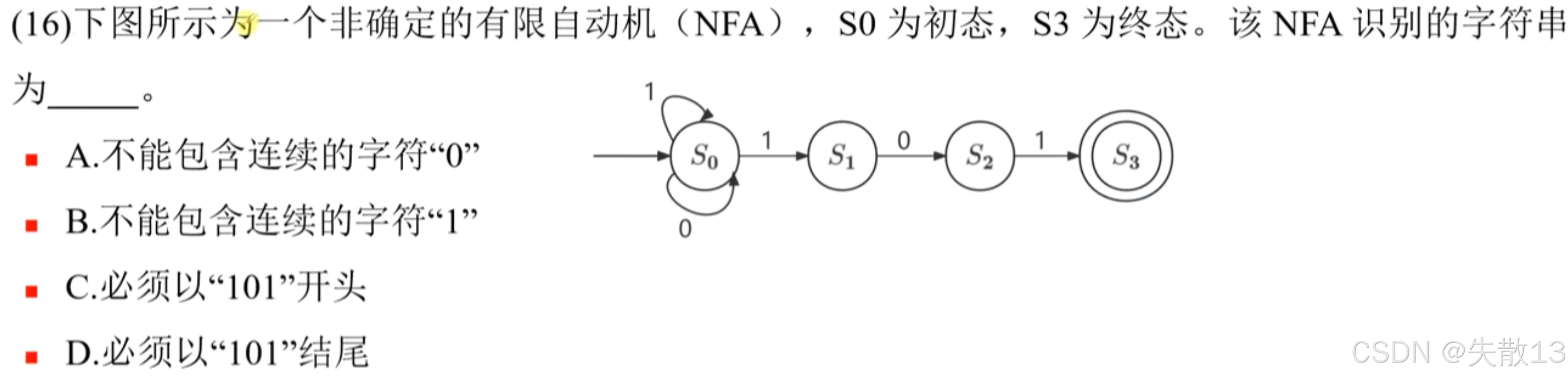
D
先转换成正规式:(0|1)*101。该自动机可以识别的字符串有1*101、0*101、1*0*101、0*1*101,这些字符串的共同特点,都是以101结尾。
2.2.6 语法分析方法
-
自上而下语法分析:采用最左推导,分析方向从左至右。给定文法GGG和源程序rrr,从GGG的开始符号SSS出发,通过反复使用产生式PPP对句型中的非终结符进行替换(推导),逐步推导出rrr;
-
递归下降分析法:其原理是利用函数之间的递归调用,模拟语法树自上而下的构造过程,属于自上而下的语法分析方法;
-
自下而上语法分析:运用最右推导,分析方向从右至左。从给定的输入串rrr开始,不断寻找子串与文法GGG中某个产生式PPP的候选式进行匹配,并用PPP的左部代替(归约)之,逐步归约到开始符号SSS;
-
移进-归约分析法:设置一个栈,将输入符号逐个移进栈中,当栈顶形成某产生式PPP的右部时,就用左部去代替,这一过程称为归约。显然,该思想是通过右部推导出左部,是自下而上语法分析的核心思想;
-
练习:对高级语言源程序进行编译或解释的过程中需要进行语法分析,递归子程序分析属于()的分析法。
- A.自上而下
- B.自下而上
- C.从左至右
- D.从右至左
A
递归下降分析法:原理是利用函数之间的递归调用,模拟语法树自上而下的构造过程,是一种自上而下的语法分析方法。
-
编译和解释:都是将高级语言翻译成计算机硬件认可的机器语言加以执行;
区别 编译 解释 目标代码 生成,并优化 不生成 独立的可执行文件 生成 不生成,逐行边翻译边执行 执行效率 较快(翻译一次,多次运行) 较慢(反复扫描源程序) 占用内存 较少 较多 灵活性 较低 较高(反复扫描源程序) 可移植性 较差 较高 -
练习:编译器与解释器是程序语言翻译的两种基本形态,以下关于编译器工作方式及特点的叙述中,正确的是()。
- A.边翻译边执行,用户程序运行效率低且可移植性差
- B.先翻译后执行,用户程序运行效率高且可移植性好
- C.边翻译边执行,用户程序运行效率低且可移植性好
- D.先翻译后执行,用户程序运行效率高且可移植性差
D
在编译方式下,会生成独立的可执行文件,与机器密切相关,因此可移植性较差。
