当前位置：首页 > news >正文

LeetCode算法日记 - Day 52: 求根节点到叶节点数字之和、二叉树剪枝

news 2025/9/25 13:44:35

1. 求根节点到叶节点数字之和

1.1 题目解析

1.2 解法

1.3 代码实现

2. 二叉树剪枝

2.1 题目解析

2.2 解法

2.3 代码实现

1. 求根节点到叶节点数字之和

求根节点到叶节点数字之和

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

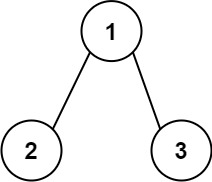
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

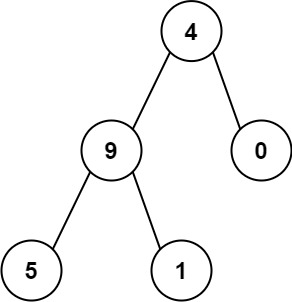
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10

1.1 题目解析

题目本质：
把“根到叶的一条路径上按十进制拼接得到一个数”，再对所有叶路径的数求和。等价为：在树上进行“路径前缀累积”，每到一个叶子，将当前前缀当作完整数字计入答案。

常规解法：
最直观的方式是：先用 DFS/BFS 找出所有根到叶的路径，拼成字符串或数组，再转成整数，最后求和。

问题分析：
上述做法需要存储所有路径（可能多达 O(叶子数) 条），并且“先保存→后转换→再求和”是多次处理，空间与常数开销都偏大。虽然总时间仍是 O(n)，但没有利用到“十进制前缀可在线累积”的性质。

思路转折：
要更高效，就不存全路径，而是在遍历时用一个前缀数在线递推：cur = presum * 10 + node.val。
当且仅当到达叶子时把 cur 加入总和即可。这样一次 DFS 完成，既避免额外容器，也减少不必要的中间转换。深度 ≤ 10，递归栈可控；若在通用工程中担心整型上界，可把累计变量换成 long（本题签名返回 int，按题设数据范围可通过）。

1.2 解法

算法思想：
• 后序/先序均可，但核心递推是一路下行维护前缀：cur = presum * 10 + node.val。
• 碰到叶子（left==null && right==null）直接返回该路径数；非叶子返回左右子树的和。
• 空指针返回 0，保证加法单位元。

i）定义递归函数 sum(node, presum)，表示从 node 出发的所有根到叶路径（以 presum 为十进制前缀）所能形成的路径数之和。

ii）递归基：node == null 返回 0。

iii）计算当前前缀：cur = presum * 10 + node.val。

iv）若 node 是叶子，返回 cur；否则返回 sum(node.left, cur) + sum(node.right, cur)。

v）入口调用 sum(root, 0)，结果即为答案。

易错点：

忘记处理 root == null 的边界：应直接返回 0。
叶子判定必须左右皆空才成立。

1.3 代码实现

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int sumNumbers(TreeNode root) {// 从根出发，前缀为 0return sum(root, 0);}// 返回以 root 为起点的所有根到叶路径所形成数字的总和，presum 为十进制前缀private int sum(TreeNode root, int presum) {if (root == null) return 0;               // 空树或空子树贡献为 0int cur = presum * 10 + root.val;         // 向下推进十进制前缀// 叶子：当前前缀就是完整的路径数字if (root.left == null && root.right == null) return cur;// 非叶子：汇总左右子树return sum(root.left, cur) + sum(root.right, cur);}
}

复杂度分析：

时间复杂度：O(n)（每个结点访问一次并进行 O(1) 推进）。
空间复杂度：O(h)（递归栈，h 为树高，题设深度 ≤ 10，最坏 O(10) ≈ 常数，若退化链则 O(n)）。

2. 二叉树剪枝

二叉树剪枝

给你二叉树的根结点 root ，此外树的每个结点的值要么是 0 ，要么是 1 。

返回移除了所有不包含 1 的子树的原二叉树。

节点 node 的子树为 node 本身加上所有 node 的后代。

示例 1：

输入：root = [1,null,0,0,1]
输出：[1,null,0,null,1]
解释：
只有红色节点满足条件“所有不包含 1 的子树”。 右图为返回的答案。

示例 2：

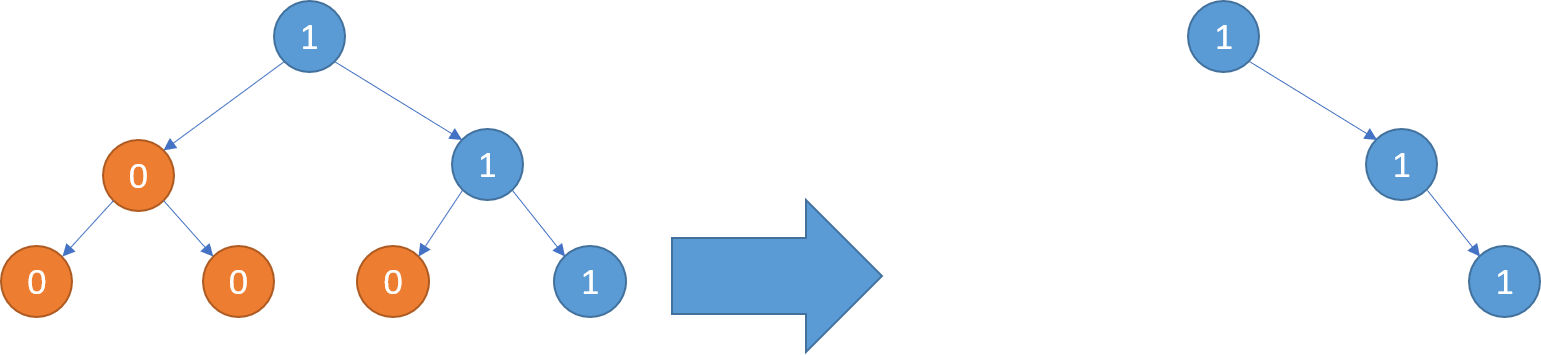
输入：root = [1,0,1,0,0,0,1]
输出：[1,null,1,null,1]

示例 3：

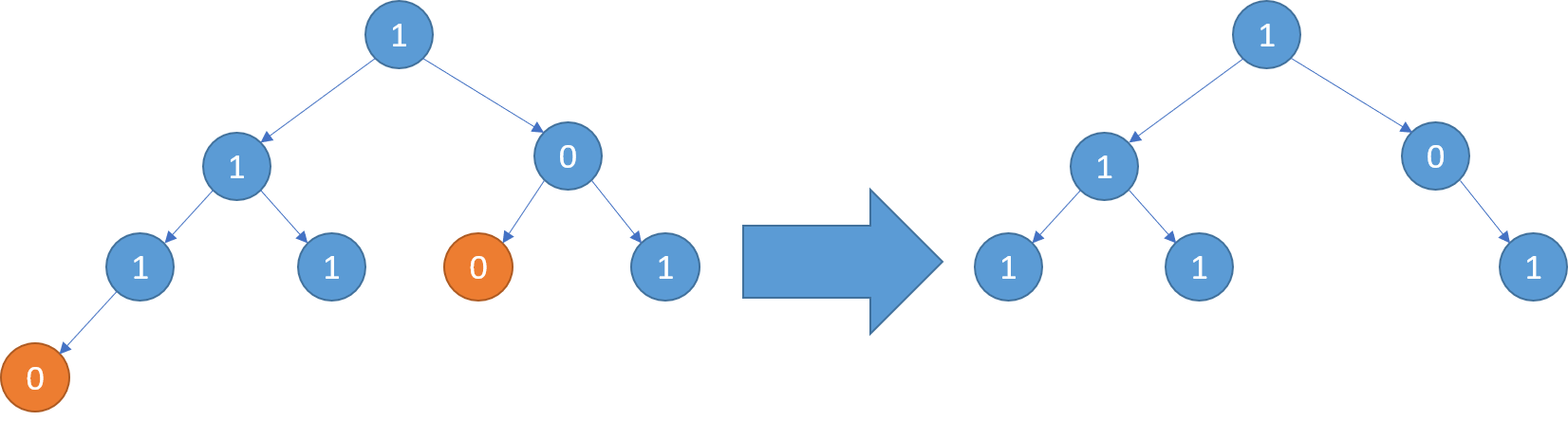
输入：root = [1,1,0,1,1,0,1,0]
输出：[1,1,0,1,1,null,1]

提示：

树中节点的数目在范围 [1, 200] 内
Node.val 为 0 或 1

2.1 题目解析

题目本质：
这是一个“按子树性质过滤”的问题。性质是：某结点的整棵子树是否包含 1。保留“包含 1”的子树，删除“不包含 1”的子树。等价表述：若某结点 val==0 且左右子树都不含 1，则这个结点也应被删掉。

常规解法：
直觉可能是对每个结点都去“数一数/查一查”它的子树里有没有 1，然后决定删不删。

问题分析：
如果每个结点都“重新遍历自己的子树”去找 1，最坏会达到 O(n^2)（很多重复扫描）。节点数最多 200 虽然也能过，但思路上冗余且不可扩展。

思路转折：
要想不重复扫描，必须 自底向上一次性计算。也就是典型的后序遍历：先处理左右子树，再回到当前结点，用“左右子树是否保留”来决定当前结点是否保留。

2.2 解法

算法思想：
后序遍历（Left → Right → Node）。设函数 prune(node) 返回修剪后的子树根：

先递归修剪左右：node.left = prune(node.left)、node.right = prune(node.right)
若 node.val == 0 且 node.left == null 且 node.right == null，则这棵子树不含 1，返回 null；
否则返回 node。

i）递归基：node == null 直接返回 null。

ii）先修剪左子树，再修剪右子树，并把结果写回到 node.left / node.right。

iii）用“当前值是 0 且左右都空”判断是否删除当前结点。

iv）返回修剪后的根（可能是原结点，也可能是 null）。

易错点：

忘记把递归结果写回：只计算 left = prune(node.left) 但没有 node.left = left（修剪不生效）。
用前序（先判断再递归）会因为信息不完整导致误判。
只处理非根结点，忘记根也可能被删（最终要返回可能为 null 的结果）。

2.3 代码实现

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode pruneTree(TreeNode root) {return prune(root);}// 后序修剪：返回修剪后的子树根private TreeNode prune(TreeNode node) {if (node == null) return null;// 先修剪左右，再决定当前node.left = prune(node.left);node.right = prune(node.right);// 当前结点为 0 且左右都空 -> 该子树不含 1，剪掉if (node.val == 0 && node.left == null && node.right == null) {return null;}return node;}
}

复杂度分析：