数据结构 之 【并查集】
目录
1. 并查集的概念
2. 并查集的核心思想
3. 并查集解决问题的类型
4. 并查集的简单实现
5. 并查集应用
1. 并查集的概念
并查集是一种处理不相交集合的数据结构,主要用于解决集合的合并与查询问题
核心操作包括:
- 查找:确定元素所属的集合(根节点)
- 合并:将两个集合合并为一个集合
这里所说的一个集合指的就是一棵树,所以并查集是森林
2. 并查集的核心思想
(1) 使用数组表示树结构,并使用双亲表示法(只能通过孩子找双亲)
数组的下标对应集合中元素的编号
初始时每个元素自成一个集合(parent[i] = -1)
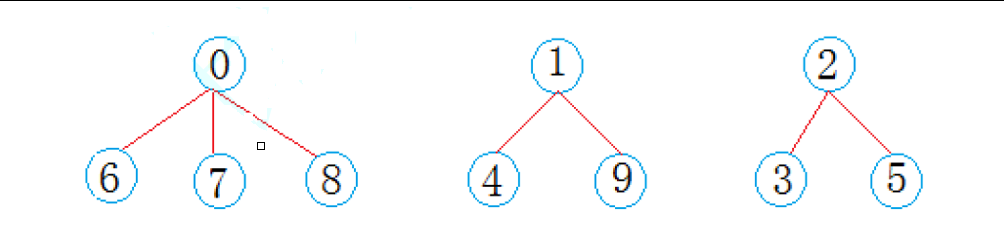
(2) 假设集合这样分类
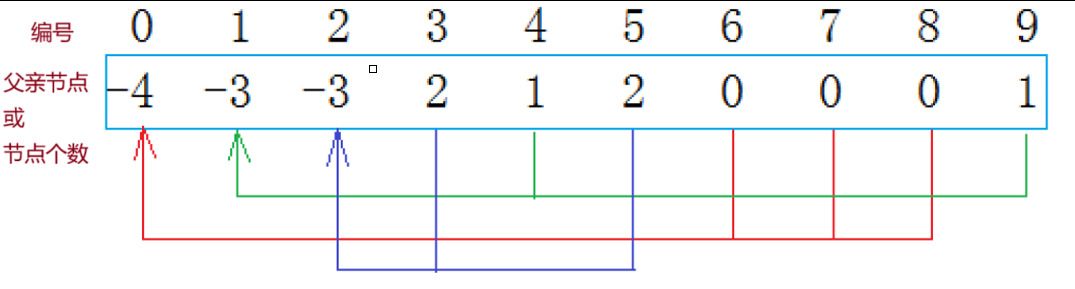
(3)那么,数组修改方法:
将孩子节点下标对应的的值加到双亲节点上,
孩子节点下标对应的的值存储双亲节点的下标
这样一来,
1.数组元素如果为负数,负号代表根,数字代表该集合中元素个数
2.数组元素如果为非负数,代表该元素双亲在数组中的下标
3. 并查集解决问题的类型
1. 查找元素属于哪个集合
用根判断元素归属,
沿着数组表示树形关系往上一直找到根(即:树中中元素为负数的位置)
2. 查看两个元素是否属于同一个集合
沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
3. 将两个集合归并成一个集合
将两个集合中的元素合并
让一个集合成为另一个集合的孩子
4. 集合的个数
遍历数组,数组中元素为负数的个数即为集合的个数。
4. 并查集的简单实现
不含路径压缩,简单合并,不按树的高度进行合并
class UnionFind {
private:vector<int> parent;//父亲节点索引
public://初始化UnionFind(int n) {}// 查找根节点int findRoot(int x) {}// 合并操作void unionSet(int x, int y) {}//判断是否在同一个集合bool InSet(int x1, int x2){}//集合个数size_t SetSize()const{}
};(1) 成员变量
使用数组vector<int> parent 存储父亲节点索引及单个集合的元素个数
(2) 默认构造函数
UnionFindSet(size_t n)
{_ufs.resize(n, -1);
}初始时,有n个根节点
(3) 查找根节点
根据节点下标,找到节点所在集合根节点的下标
//找根节点下标
int FindRoot(int x)
{while (parent[x] >= 0)//判断是否是根{x = parent[x];//迭代父亲节点}return x;
}(4) 将两个元素并入一个集合
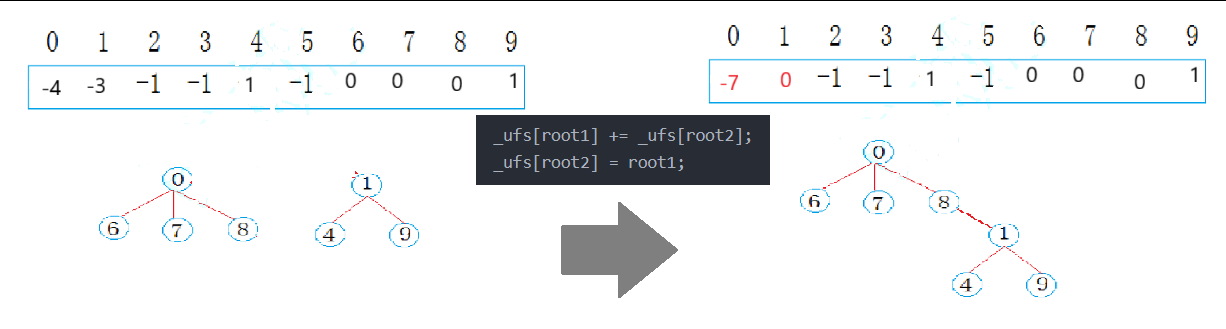
合并的思路:如果两个元素所在集合不同,将一个集合的根节点作为另一个集合的孩子节点
这里为了简单,并未按秩合并(树的高度)
void Union(int x1, int x2)
{int root1 = FindRoot(x1);int root2 = FindRoot(x2);//在同一个集合就不必要合并if (root1 == root2)return;//将孩子节点下标对应的的值加到双亲节点上,//孩子节点下标对应的的值存储双亲节点的下标_ufs[root1] += _ufs[root2];_ufs[root2] = root1;
}
(5)是否在同一个集合、集合个数
//是否在同一个集合
bool InSet(int x1, int x2)
{return FindRoot(x1) == FindRoot(x2);
}
//集合个数
size_t SetSize()
{int count = 0;for (auto& e : _ufs){if (e < 0)count++;}return count;
}两个元素是否在同一个集合,即判断两者的根节点是否一致
集合个数就是数组中负数的个数
5. 并查集应用
LCR 116. 省份数量 - 力扣(LeetCode)
两个城市相连则可以认为两个城市在一个集合当中,合并城市下标
class Solution {
public:int findCircleNum(vector<vector<int>>& isConnected) {vector<int> ufs(isConnected.size(), -1);//存放父亲索引auto FindRoot = [&ufs](int x){//查找根节点while(ufs[x] >= 0)x= ufs[x];return x;};//相连的城市进入同一个集合for(int i = 0; i < isConnected.size(); ++i){for(int j = 0; j < isConnected[i].size(); ++j){if(isConnected[i][j] == 1){int root1 = FindRoot(i);int root2 = FindRoot(j); if(root1 != root2){ufs[root1] += ufs[root2];ufs[root2] =root1;}}}}//集合的个数int count = 0;for(auto& e: ufs){if(e < 0)++count;}return count;}
};990. 等式方程的可满足性 - 力扣(LeetCode)
两个变量相等则可以认为两个变量在同一个集合
class Solution {
public:bool equationsPossible(vector<string>& equations) {vector<int> ufs(26, -1);//存放父亲索引auto FindRoot = [&ufs](int x)//查找根节点{int root = x;while(ufs[root] >= 0){root = ufs[root];}return root;};//相等的变量进入同一个集合for(auto& str: equations){if(str[1] == '='){//通过根节点进入同一个集合int root1 = FindRoot(str[0] - 'a');int root2 = FindRoot(str[3] - 'a');if(root1 != root2){ufs[root1] += ufs[root2];ufs[root2] = root1;}}}//判断for(auto& str: equations){if(str[1] == '!'){int root1 = FindRoot(str[0] - 'a');int root2 = FindRoot(str[3] - 'a');//在一个集合里面就不符合规定if(root1 == root2){return false;}}}return true;}
};