斯坦福Percy Liang团队：如果有足够显卡，如何设计最佳预训练策略？

Pre-training under infinite compute

• ArXiv URL: http://arxiv.org/abs/2509.14786v1

• 作者: Percy Liang; Tatsunori Hashimoto; Konwoo Kim; Suhas Kotha

• 发布机构: Stanford University

本文提出，在数据受限而计算资源无限的未来场景下，通过深度优化正则化、模型集成和知识蒸馏等经典算法，可以显著提升语言模型预训练的数据效率，其效果远超单纯增加训练轮次或模型参数的传统方法。

关键定义

本文的核心是围绕在数据受限、计算无限的假设下如何进行预训练，并为此提出或重新审视了几个关键概念：

• 标准配方 (Standard Recipe): 指当前数据受限场景下的常规做法，即重复使用数据（增加epoch）和增加模型参数数量。本文指出这种方法会很快遭遇过拟合瓶颈。
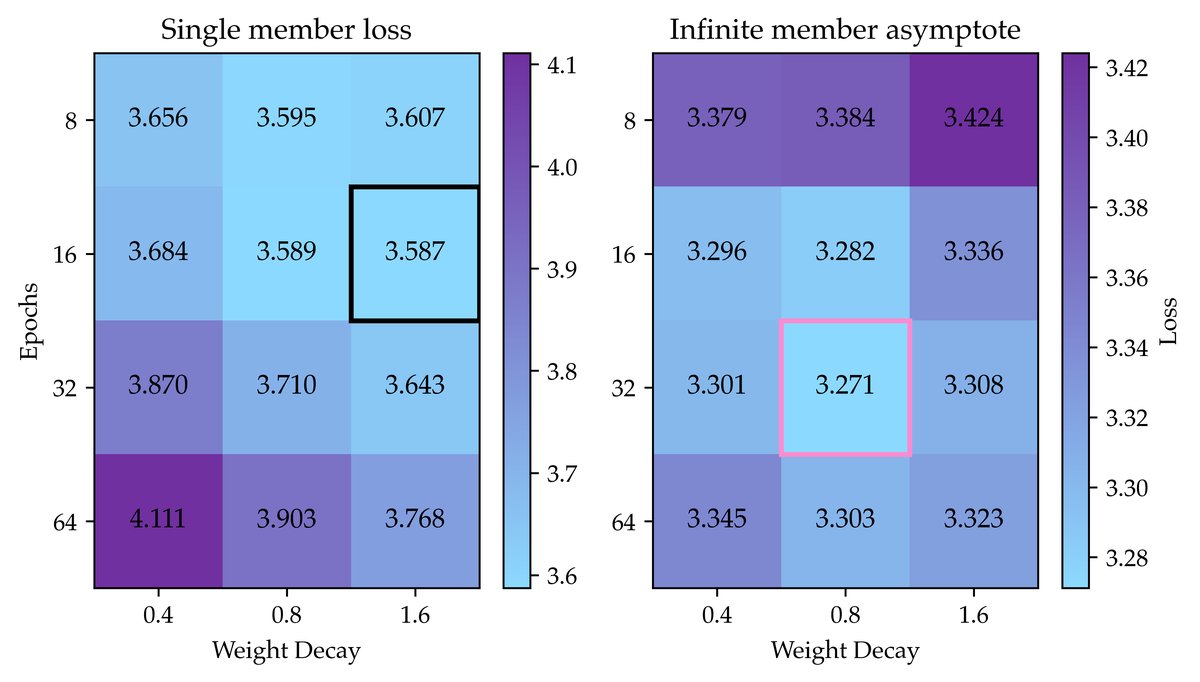
• 正则化配方 (Regularized Recipe): 本文提出的第一个改进方法。通过对权重衰减（weight decay）、学习率和训练轮次进行联合精调（发现最优权重衰减比常规值大30倍），使得模型损失能够随着参数量的增加而单调下降，避免了过拟合。
• 集成配方 (Ensembling Recipe): 本文提出的另一个更优的方法。与训练单个大模型不同，该方法独立训练 K 个较小的模型，并在推理时平均它们的 logits 输出。
• 缩放定律的渐近线 (Asymptote of a Scaling Law): 本文提出的一个核心评估指标。由于计算资源无限，评估一个方法的优劣不应看其在特定计算预算下的表现，而应看其缩放定律（Scaling Law）在资源（如参数量N或集成成员数K）趋于无穷时的理论极限（即渐近线 E_D）。更低的渐近线意味着该方法在理论上能达到的性能上限更高。
• 数据效率 (Data Efficiency): 衡量算法优越性的指标。指为了达到相同的模型性能（损失），一个算法（如正则化配方）所需的原始数据量，与基准算法（如标准配方）所需数据量的比值。例如，数据效率为 5x 意味着用 1/5 的数据就能达到相同的效果。

相关工作

当前语言模型预训练的缩放定律（如Chinchilla）通常建立在计算资源受限但数据（几乎）无限的假设之上，推荐按比例增加模型大小和数据量。然而，现实是计算能力的增长速度（每年4倍）远超网络文本数据的增长速度（每年1.03倍），这意味着未来预训练将越来越多地受到数据量的限制。

在数据受限的情况下，简单的应对策略如重复数据（增加训练轮次）或持续增大模型规模，会导致模型在训练集上过拟合，验证损失不降反升，从而限制了模型性能的上限。

本文旨在解决的核心问题是：当数据量固定而计算资源不受限制时，应该如何设计预训练策略以达到最佳的模型性能？ 作者不以计算成本为考量，而是探索不同算法能够从固定数据中“压榨”出信息的理论极限。

本文方法

标准配方的局限性

本文首先验证了当前数据受限下的标准做法存在瓶颈。在一个固定的200M tokens数据集上，无论是单纯增加训练轮次（epoch），还是增加模型参数量，最终都会导致验证损失因过拟合而上升。这表明，在没有无限新数据的情况下，盲目堆砌计算资源并不能持续提升模型性能。

](https://raw.githubusercontent.com/agifrontier/agifrontier.github.io/main/images/2509.14786v1/ablation_lr_tuned_epoch.jpg)

创新点1：正则化参数缩放

为了克服标准配方的过拟合问题，本文提出了正则化配方。其核心创新在于对正则化参数进行精细调整。通过坐标下降法对权重衰减（weight decay）、学习率和训练轮次进行联合寻优，发现对于过参数化的模型，最优的权重衰减值比常规实践（0.1）高出30倍以上。

经过充分正则化后，模型损失随着参数量 N 的增加呈现出单调下降的趋势，并能很好地拟合一个幂律（Power Law）公式：

$${\hat{\mathcal{L}}}_{D,N}\ne \frac{A_D}{N^{{\alpha }_D}}+E_D$$

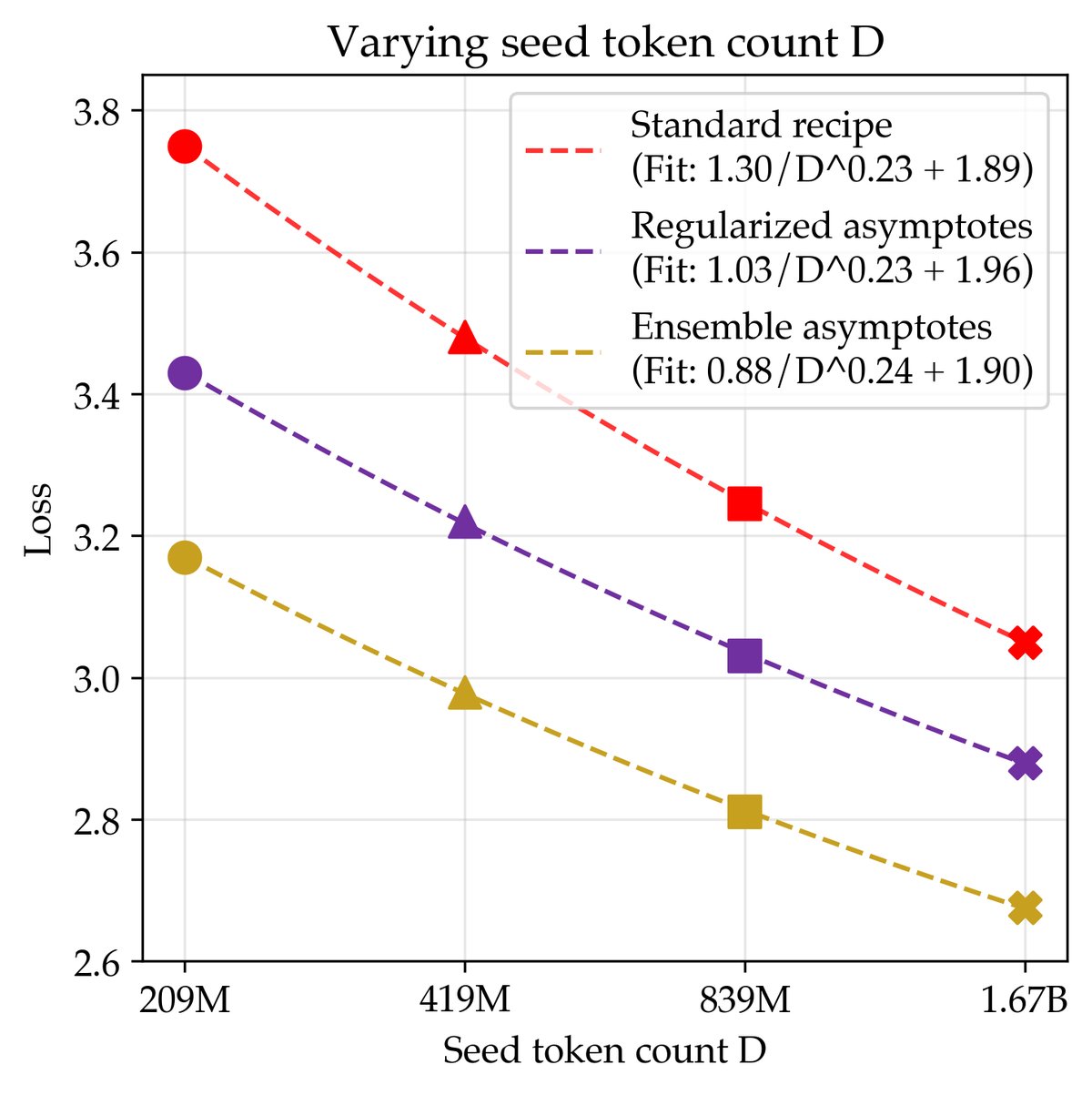
其中 E_D 是损失的渐近线，代表了该方法在参数量 N 趋于无穷时的理论最佳性能。通过这种方式，本文提出了一种新的评估标准：用缩放定律的渐近线来衡量一个方法的好坏。对于200M tokens数据，正则化配方的渐近线损失为3.43。

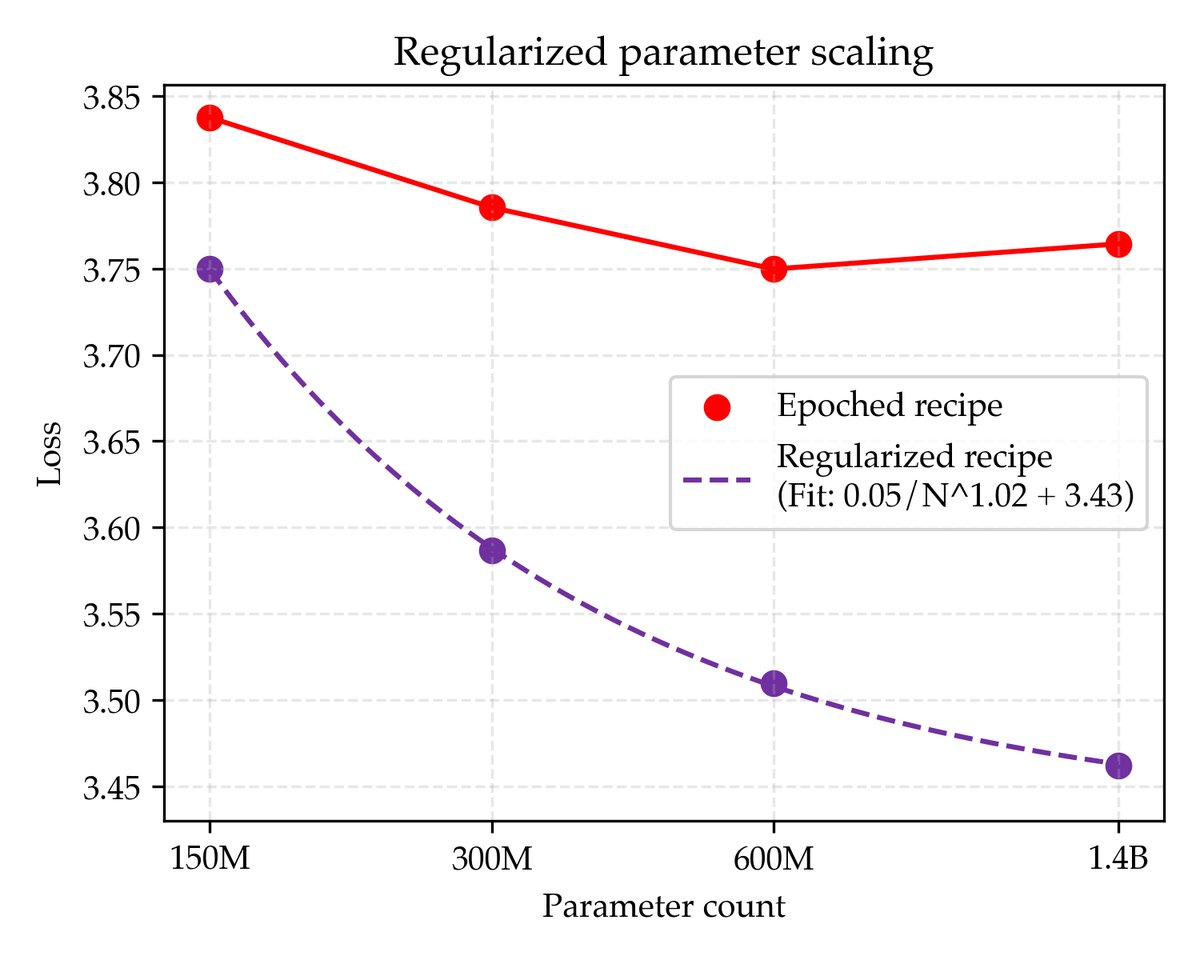
尽管正则化参数缩放有效，但它是否是理论上的最优解？本文接着探索了集成配方，即独立训练 K 个模型并平均它们的 logits。

实验发现，当总参数量 NK 相同时，扩展集成成员数 K 比扩展单个模型的参数量 N 能达到更低的损失渐近线。如图所示，一个由多个300M模型组成的集成，其损失渐近线（3.34）优于单个模型参数量趋于无穷时的渐近线（3.43）。这表明，当计算资源足够时，训练多个小模型通常比训练一个超大模型更优。

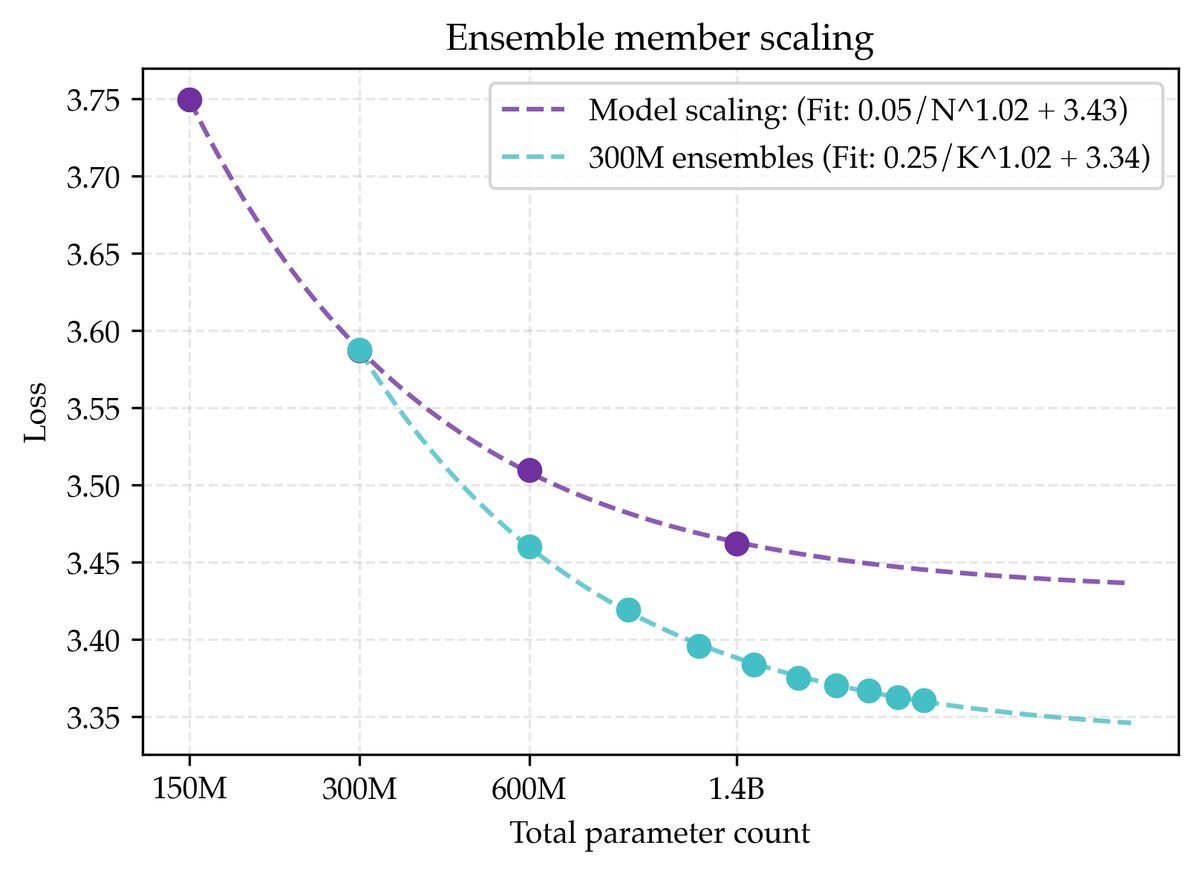
本文将参数缩放和集成缩放结合，提出了联合缩放配方 (Joint Scaling Recipe)，目标是估计 N→∞ 和 K→∞ 时的极限损失。这通过一个分两步的极限过程实现：

1. 对于固定的 N，通过拟合幂律估计 K→∞ 时的渐近线损失。
2. 将第一步得到的多个渐近线（对应不同 N）再次拟合幂律，估计 N→∞ 时的最终渐近线。

通过这种方法，在200M tokens数据上，联合缩放配方的理论最佳损失为3.17，显著优于正则化配方（3.43）和标准配方（3.75）。

创新点4：通过蒸馏实现参数效率

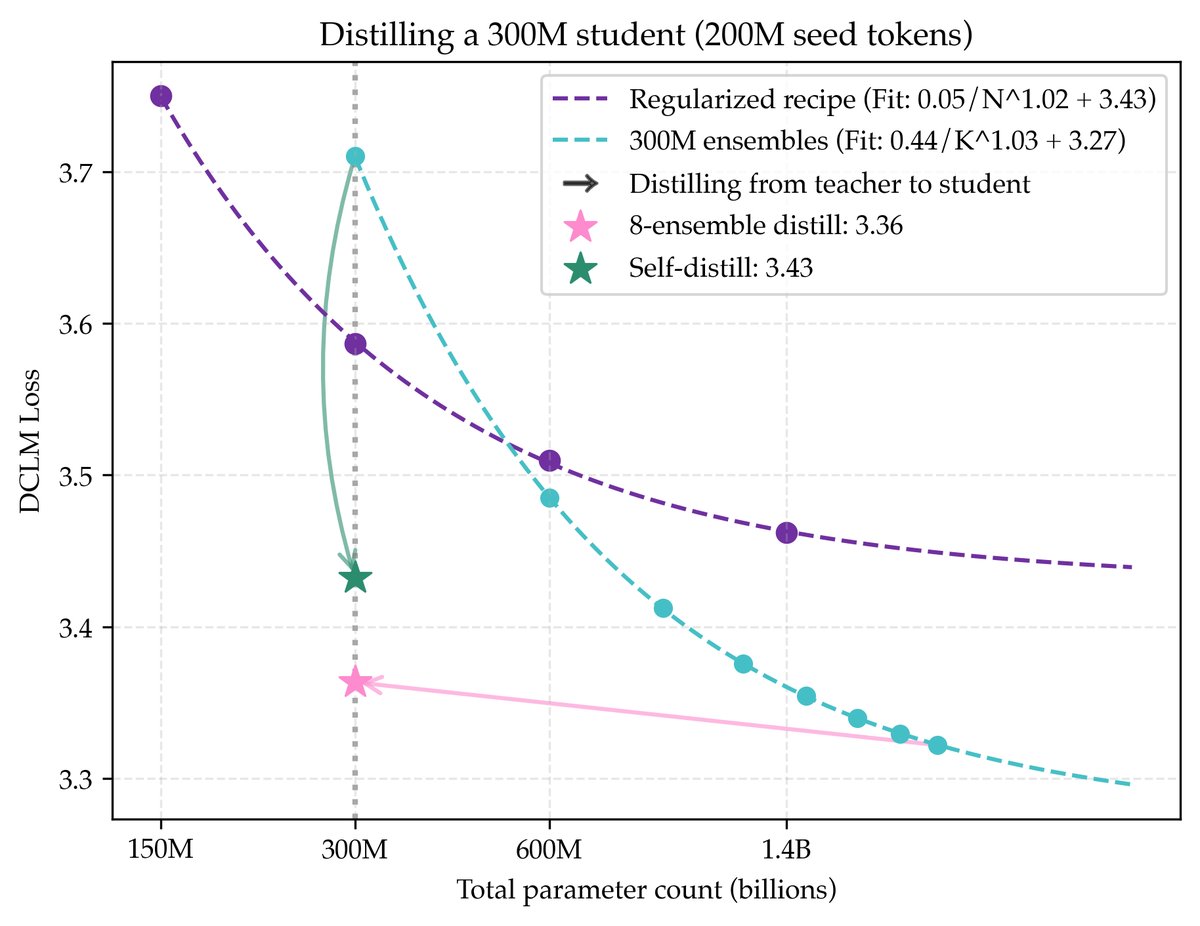
集成和超大模型虽然性能好，但推理成本高昂。本文展示了如何通过知识蒸馏 (Knowledge Distillation) 在不牺牲太多性能的情况下降低模型参数量。

• 集成蒸馏: 将一个由8个300M模型组成的集成（总参数2.4B）蒸馏到一个300M的学生模型中，学生模型保留了83%的性能增益，其性能甚至超过了参数缩放配方的理论极限。
• 自蒸馏 (Self-distillation): 更令人惊讶的是，将一个300M模型蒸馏到一个同样大小和架构的新学生模型中，也能显著提升性能。这表明，即使在训练过程中也不需要引入更大的模型，就能实现数据效率的提升。

数据效率增益

本文通过在200M、400M、800M和1.6B tokens 这四个不同量级的数据集上重复上述实验，验证了其方法的普适性。

• 数据效率衡量: 在200M tokens数据集上，正则化配方的数据效率是标准配方的2.29倍，而联合缩放配方的数据效率高达5.17倍。这意味着仅用约1/5的数据，联合缩放配方就能达到标准配方在无限计算下的最佳性能。
• 增益的持续性: 数据缩放定律表明，这些数据效率的提升在更大的数据集规模上依然存在。所有三种配方（标准、正则化、联合）的数据缩放曲线斜率相似，表明效率增益是一个近似恒定的乘数因子。

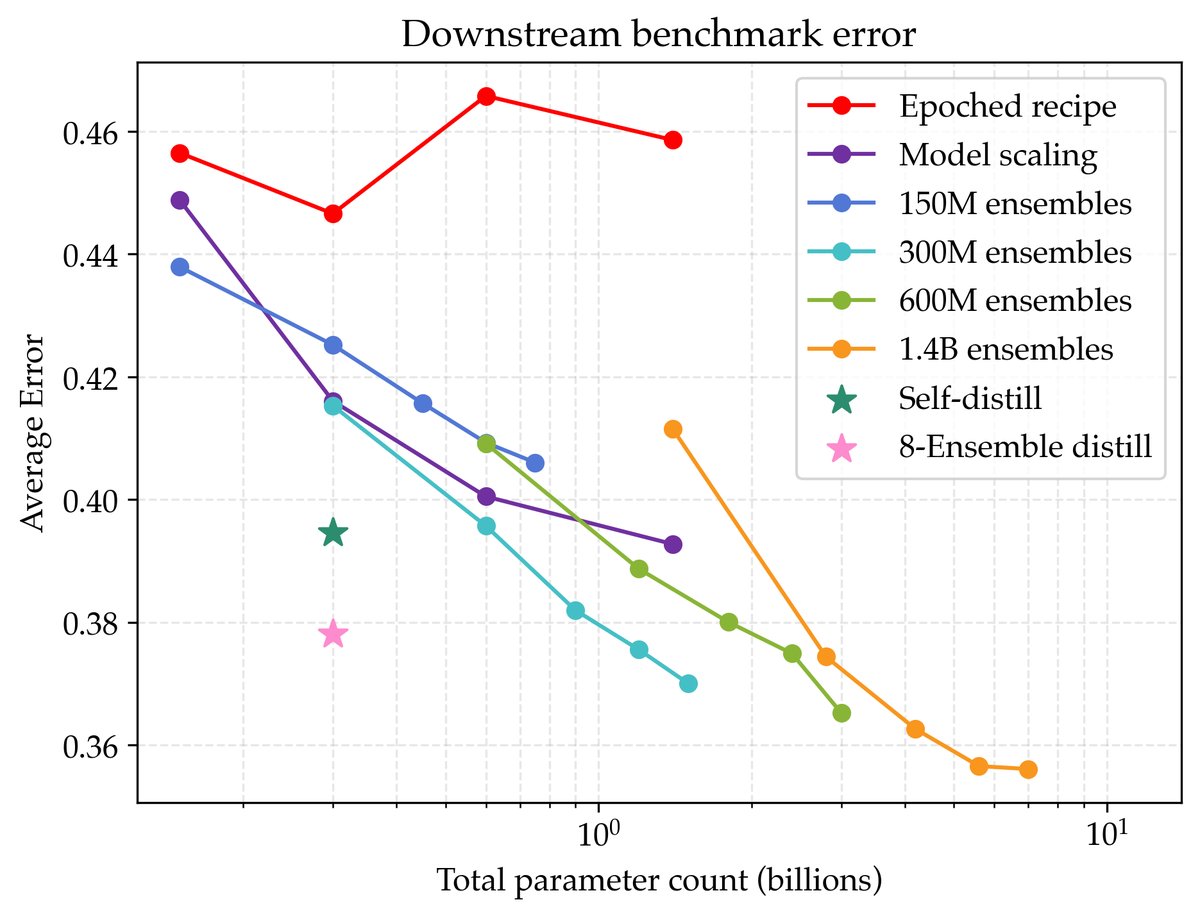
验证损失的降低确实转化为了实际能力的提升。

• 本文在PIQA、SciQ和ARC Easy 等标准基准上进行了评测。结果显示，验证损失更低的模型在下游任务上的平均错误率也更低。
• 最佳的集成模型比最佳的非正则化基线模型平均性能高出9%。经蒸馏得到的300M模型也比同等规模的基线模型性能高出7%。

本文的方法可以直接应用于持续预训练（CPT）场景。在一个数学推理任务中，作者仅使用4B tokens的数据对Llama 3.2 3B模型进行CPT。

• 通过采用文中的epoching和集成策略（8个模型的集成），其性能超过了使用完整73B tokens数据进行标准CPT的基线模型。
• 这实现了惊人的17.5倍数据效率提升，证明了本文发现在实际应用场景中的巨大潜力。

模型	数据 (Tokens)	使用的Tokens	GSM8K	MATH	MathQA	平均准确率
基线
Llama 3.2 3B Base	0B	N/A	3.64	2.50	17.06	7.73
默认CPT (来自原论文)	73B	73B	5.38	3.12	29.56	12.69
本文方法 (4B Tokens)
默认CPT	4B	4B	4.85	3.42	27.94	12.07
单模型（K=1，优化后）	4B	32B	8.87	3.75	34.62	15.75
8模型集成（K=8）	4B	256B	14.63	4.88	36.31	18.61

总结

本文系统性地证明了，在未来数据成为瓶颈而计算资源充裕的时代，我们应当重新审视并优化经典的训练算法。通过精细的正则化、模型集成和知识蒸馏，可以在固定的数据上实现远超传统方法的性能，从而极大地提高数据效率。这些看似简单的算法改进，为未来的语言模型预训练指明了一条更加高效和强大的路径。