「日拱一码」099 数据处理——降维
目录
什么是降维?
为什么需要降维?
主要降维方法
1. 线性降维
2. 非线性降维
代码示例
关键要点
实际应用场景
什么是降维?
降维是将高维数据转换为低维表示的过程,旨在保留数据的主要结构和特征,同时减少数据的复杂度。当数据特征数量非常多时(即"维数灾难"),降维技术变得尤为重要。
为什么需要降维?
- 可视化:将高维数据降至2D或3D以便可视化展示
- 去除冗余:消除相关特征和噪声
- 提高效率:减少计算和存储成本
- 防止过拟合:简化模型,提高泛化能力
- 特征提取:发现数据的内在结构
主要降维方法
1. 线性降维
- 主成分分析 (PCA):寻找最大方差方向
- 线性判别分析 (LDA):考虑类别信息的监督降维
- 奇异值分解 (SVD):矩阵分解方法
- 因子分析:寻找潜在变量
2. 非线性降维
- t-SNE:保持局部结构的可视化方法
- UMAP:保持全局和局部结构
- 自编码器:神经网络方法
- 等距映射 (Isomap):保持测地距离
代码示例
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris, make_swiss_roll
from sklearn.decomposition import PCA, KernelPCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.manifold import TSNE, Isomap, MDS
from sklearn.preprocessing import StandardScaler
from sklearn.random_projection import GaussianRandomProjection# 设置样式
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
sns.set_style("whitegrid")# 1. 加载数据
print("加载鸢尾花数据集...")
iris = load_iris()
X = iris.data
y = iris.target
feature_names = iris.feature_names
target_names = iris.target_namesprint(f"原始数据形状: {X.shape}") # (150, 4)
print(f"特征名称: {feature_names}") # ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)# 2. 主成分分析 (PCA)
print("\n=== 主成分分析 (PCA) ===")
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)print(f"解释方差比例: {pca.explained_variance_ratio_}") # [0.72962445 0.22850762]
print(f"累计解释方差: {np.cumsum(pca.explained_variance_ratio_)}") # [0.72962445 0.95813207]# 3. 线性判别分析 (LDA)
print("\n=== 线性判别分析 (LDA) ===")
lda = LDA(n_components=2)
X_lda = lda.fit_transform(X_scaled, y)
print(f"解释方差比例: {lda.explained_variance_ratio_}") # [0.9912126 0.0087874]# 4. t-SNE 降维
print("\n=== t-SNE 降维 ===")
tsne = TSNE(n_components=2, random_state=42, perplexity=30)
X_tsne = tsne.fit_transform(X_scaled)# 5. 可视化比较
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
fig.suptitle('不同降维方法比较 - 鸢尾花数据集', fontsize=16, fontweight='bold')methods_data = [(X_pca, 'PCA', '主成分1', '主成分2'),(X_lda, 'LDA', 'LD1', 'LD2'),(X_tsne, 't-SNE', 't-SNE1', 't-SNE2')
]for i, (data, title, xlabel, ylabel) in enumerate(methods_data):row, col = i // 2, i % 2scatter = axes[row, col].scatter(data[:, 0], data[:, 1], c=y,cmap='viridis', alpha=0.7, s=50)axes[row, col].set_title(title)axes[row, col].set_xlabel(xlabel)axes[row, col].set_ylabel(ylabel)axes[row, col].grid(True, alpha=0.3)# 方差解释率
pca_full = PCA().fit(X_scaled)
cumulative_variance = np.cumsum(pca_full.explained_variance_ratio_)
axes[1, 1].plot(range(1, 5), cumulative_variance, 'bo-')
axes[1, 1].set_title('PCA累计方差解释率')
axes[1, 1].set_xlabel('主成分数量')
axes[1, 1].set_ylabel('累计解释方差比例')
axes[1, 1].grid(True, alpha=0.3)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.tight_layout()
plt.show()# 6. 选择最佳降维维度
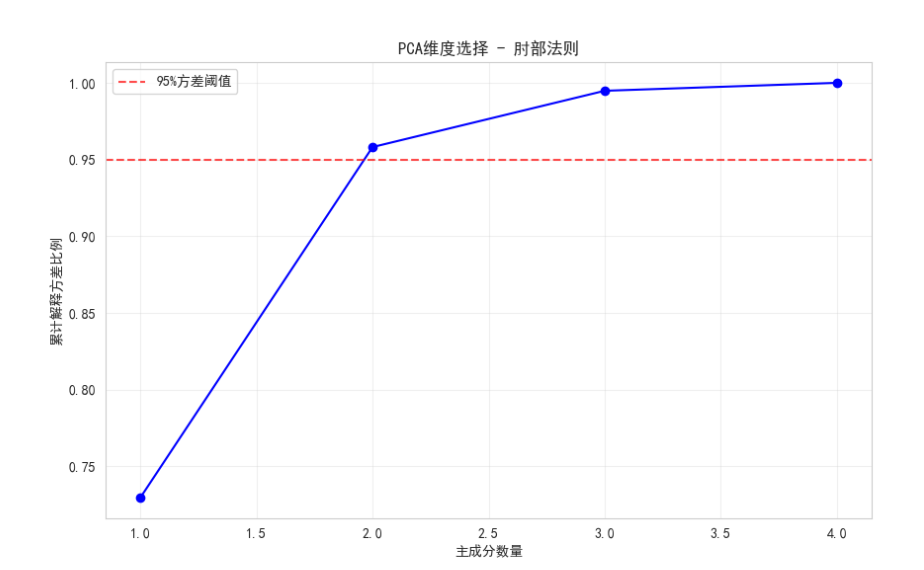
print("\n=== 选择最佳降维维度 ===")
pca = PCA()
pca.fit(X_scaled)plt.figure(figsize=(10, 6))
plt.plot(range(1, 5), np.cumsum(pca.explained_variance_ratio_), 'bo-')
plt.axhline(y=0.95, color='r', linestyle='--', alpha=0.7, label='95%方差阈值')
plt.xlabel('主成分数量')
plt.ylabel('累计解释方差比例')
plt.title('PCA维度选择 - 肘部法则')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()# 选择保留95%方差的维度
n_components = np.argmax(np.cumsum(pca.explained_variance_ratio_) >= 0.95) + 1
print(f"保留95%方差所需维度: {n_components}") # 2# 7. 非线性数据降维示例
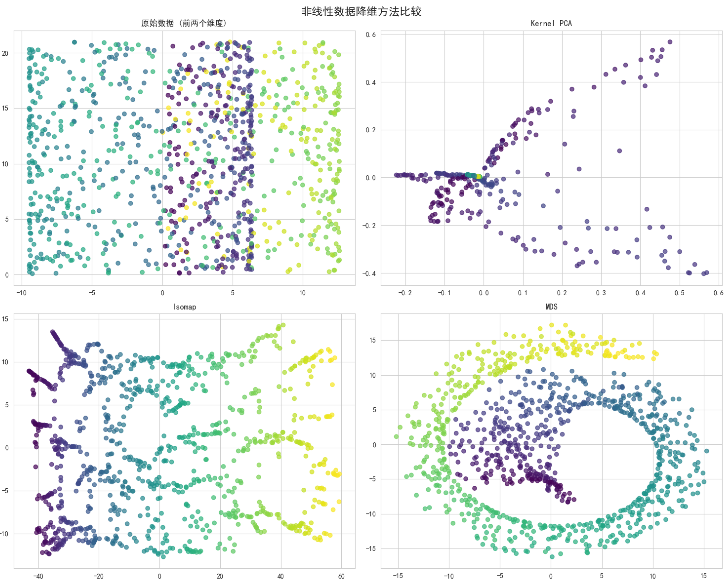
print("\n=== 非线性数据降维 ===")
X_swiss, color = make_swiss_roll(n_samples=1000, random_state=42)# 应用不同非线性降维方法
nonlinear_methods = {'Kernel PCA': KernelPCA(n_components=2, kernel='rbf'),'Isomap': Isomap(n_components=2),'MDS': MDS(n_components=2, random_state=42)
}fig, axes = plt.subplots(2, 2, figsize=(15, 12))
fig.suptitle('非线性数据降维方法比较', fontsize=16, fontweight='bold')# 原始数据前两个维度
axes[0, 0].scatter(X_swiss[:, 0], X_swiss[:, 1], c=color, cmap='viridis', alpha=0.7)
axes[0, 0].set_title('原始数据 (前两个维度)')for i, (name, method) in enumerate(nonlinear_methods.items()):row, col = (i + 1) // 2, (i + 1) % 2X_reduced = method.fit_transform(X_swiss)axes[row, col].scatter(X_reduced[:, 0], X_reduced[:, 1], c=color,cmap='viridis', alpha=0.7)axes[row, col].set_title(name)plt.tight_layout()
plt.show()# 8. 实际应用:降维后的机器学习流程
print("\n=== 降维在机器学习中的应用 ===")
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 原始数据
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42
)# 使用PCA降维
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train)
X_test_pca = pca.transform(X_test)# 训练分类器
clf_original = RandomForestClassifier(random_state=42)
clf_pca = RandomForestClassifier(random_state=42)clf_original.fit(X_train, y_train)
clf_pca.fit(X_train_pca, y_train)# 评估性能
acc_original = accuracy_score(y_test, clf_original.predict(X_test))
acc_pca = accuracy_score(y_test, clf_pca.predict(X_test_pca))print(f"原始数据准确率: {acc_original:.4f}")
print(f"PCA降维后准确率: {acc_pca:.4f}")
print(f"维度减少: {X.shape[1]} -> {X_train_pca.shape[1]}")
print(f"准确率变化: {acc_original - acc_pca:+.4f}")
# 原始数据准确率: 1.0000
# PCA降维后准确率: 0.9000
# 维度减少: 4 -> 2
# 准确率变化: +0.1000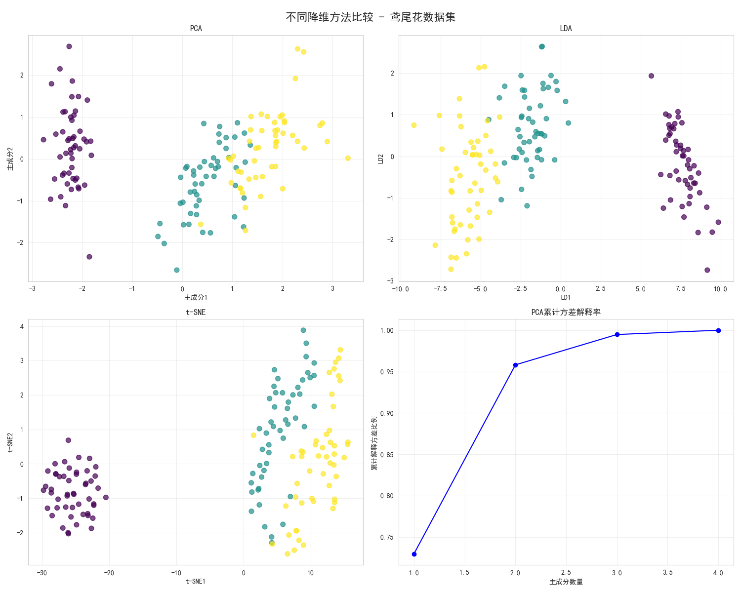
关键要点
- 数据预处理:降维前务必进行数据标准化
- 维度选择:使用累计方差解释率选择合适维度
- 方法选择:根据数据特性和任务目标选择合适方法
- 性能评估:降维后应评估对模型性能的影响
- 可视化验证:通过可视化检查降维效果
实际应用场景
- 图像处理:将高维像素数据降维
- 文本分析:处理词向量和高维文本特征
- 生物信息学:处理基因表达数据
- 推荐系统:处理用户-物品交互矩阵
- 异常检测:在高维空间中识别异常点
