逻辑回归（四）：从原理到实战-训练，评估与应用指南

引言：

上期我们完成了数据可视化，本期内容，我们将从探索分析正式迈向机器学习的核心环节——模型训练与评估。我们将亲手赋予算法学习的能力，并像一位严谨的审计官一样，全方位地评估它的性能。

Step1:构建预测模型（用逻辑回归）

log_reg = LogisticRegression(random_state=42)
log_reg.fit(X_train, y_train)
y_pred_log_reg = log_reg.predict(X_test)

代码解析：

log_reg = LogisticRegression(random_state=42)

log_reg = LogisticRegression(...): 实例化了一个 LogisticRegression 类别的对象，并将其赋值给变量 log_reg。

LogisticRegression: 这是 sklearn.linear_model 模块中提供的逻辑回归分类器。

random_state=42: 这是一个随机状态种子。在一些机器学习算法中（包括逻辑回归在某些内部实现时），可能会用到随机数生成。设置 random_state 目的是为了保证每次运行代码时，随机数生成器的起始状态都是相同的。这使得实验结果具有可复现性，即当你对模型进行训练和预测时，总是会得到相同的结果（前提是所有输入数据和参数都相同）。42 是一个常用的、任意选择的整数。

log_reg.fit(X_train, y_train)

• log_reg.fit(...): 这是模型训练的核心方法。它使用训练数据来“学习”参数，从而建立输入特征与目标变量之间的关系。
• X_train: 这是训练集的特征数据。在前面的代码中，X 是所有特征，经过 train_test_split 划分后，X_train 包含了用于训练模型的那部分特征。这些特征在前面已经被 StandardScaler 进行过标准化处理，所以这里传入的是标准化后的特征。
• y_train: 这是训练集的目标变量（标签）。与 X_train 对应，y_train 包含了训练集样本的真实类别（在前面已经通过 LabelEncoder 转换成了数值）。
• 作用: fit 方法会根据 X_train 和 y_train 来调整逻辑回归模型内部的权重（系数）和偏置项，使得模型能够尽可能准确地预测 y_train 的值。

y_pred_log_reg = log_reg.predict(X_test)

• y_pred_log_reg = log_reg.predict(...): 这是模型进行预测的方法。它使用已经训练好的模型来预测新数据（测试集）的类别。
• log_reg: 这是已经通过 .fit() 方法训练好的逻辑回归模型对象。
• X_test: 这是测试集的特征数据。与 X_train 类似，X_test 是从原始特征 X 中划分出来，用于评估模型在未见过的数据上的表现。同样，这里传入的是经过 StandardScaler 标准化处理后的测试集特征。
• y_pred_log_reg: 这是预测结果的变量。.predict() 方法会返回一个数组，其中包含了模型对 X_test 中每一个样本预测出的类别标签（数值形式）。

Step2:评估逻辑回归模型

# 评估逻辑回归模型
accuracy_log_reg = accuracy_score(y_test, y_pred_log_reg)
cm_log_reg = confusion_matrix(y_test, y_pred_log_reg)
cr_log_reg = classification_report(y_test, y_pred_log_reg, target_names=le.classes_)

代码解析：

accuracy_log_reg = accuracy_score(y_test, y_pred_log_reg)

• accuracy_log_reg = accuracy_score(...): 这一行计算模型的准确率。
• accuracy_score: 这是 sklearn.metrics 模块中的一个函数，用于计算分类模型的准确率。
• y_test: 这是测试集的真实目标变量（真实标签）。
• y_pred_log_reg: 这是模型对测试集进行的预测目标变量。
• 作用: accuracy_score 会比较 y_test 和 y_pred_log_reg 中对应位置的元素。它计算预测正确的样本数占总测试样本数的比例，并将结果（一个浮点数，介于 0 和 1 之间）赋值给 accuracy_log_reg。

cm_log_reg = confusion_matrix(y_test, y_pred_log_reg)

• confusion_matrix(y_test, y_pred_log_reg): 计算混淆矩阵。

cr_log_reg = classification_report(y_test, y_pred_log_reg, target_names=le.classes_)

• classification_report(y_test, y_pred_log_reg, target_names=le.classes_): 生成详细的分类报告。target_names=le.classes_ 参数使得报告中的类别名称是原始的字符串名称，而不是数字编码。

Step3：打印混淆矩阵和分类报告

print("\n--- 逻辑回归模型评估 ---")
print(f"准确率: {accuracy_log_reg:.4f}")
print("\n混淆矩阵:")
print(cm_log_reg)
print("\n分类报告:")
print(cr_log_reg)

结果如下：

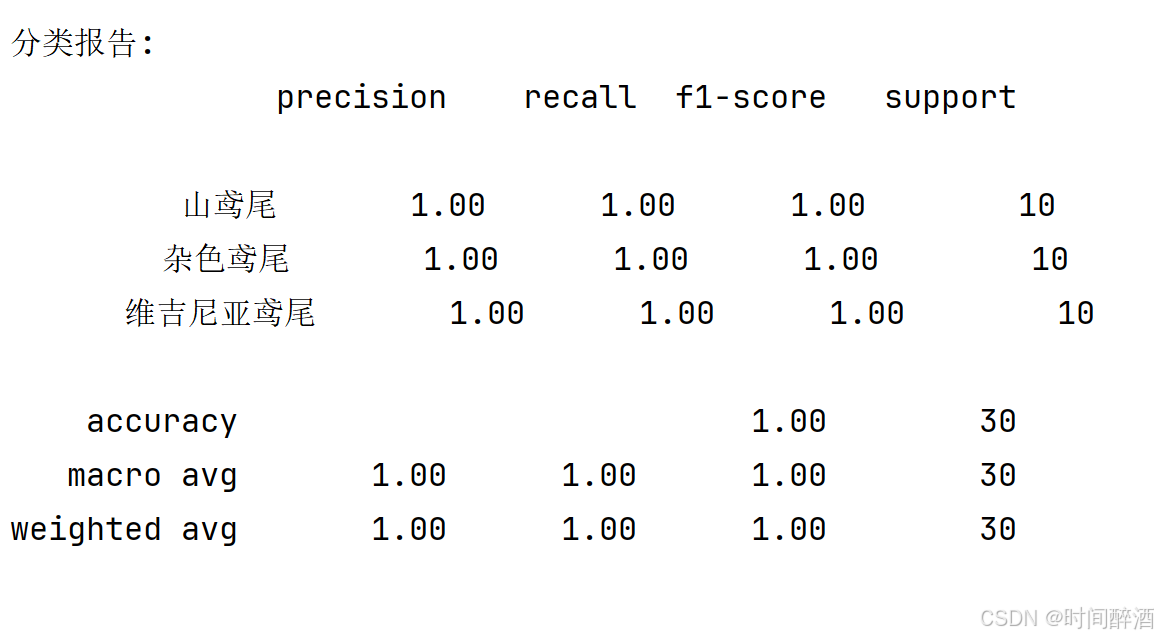
Step4:分析结果：

在分析之前，我想先介绍一下各指标的含义

1. 混淆矩阵 (Confusion Matrix)

混淆矩阵是一个 NxN 的矩阵，其中 N 是类别的数量。它直观地展示了模型在各个类别上的预测结果，究竟哪些样本被正确分类，哪些被错误分类，以及错误分类到哪个类别。

对于一个二分类问题（通常分为“正例”和“负例），混淆矩阵是一个 2x2 的矩阵，包含以下四个基本要素：

• 真正例 (True Positive, TP): 模型正确地预测为正类的样本数量。

  • 真实标签：正类
  • 模型预测：正类

• 真负例 (True Negative, TN): 模型正确地预测为负类的样本数量。

  • 真实标签：负类
  • 模型预测：负类

• 假正例 (False Positive, FP): 模型错误地预测为正类的样本数量 (实际是负类)。也称为 第一类错误 (Type I Error)。

  • 真实标签：负类
  • 模型预测：正类

• 假负例 (False Negative, FN): 模型错误地预测为负类的样本数量 (实际是正类)。也称为 第二类错误 (Type II Error)。

  • 真实标签：正类
  • 模型预测：负类

混淆矩阵的图形表示 (以二分类为例):

        Predicted Positive | Predicted Negative
----------------------------------------------
Actual Positive |        TP              |        FN
----------------------------------------------
Actual Negative |        FP              |        TN

对于多分类问题: N x N 的维度，其中 N 是类别的数量。

• 对角线上的元素表示正确分类的样本。
• 非对角线上的元素表示错误分类的样本，其具体值表示被错误预测到某个类别的样本数量。

混淆矩阵的用途:

• 直观展示分类情况: 快速了解模型在哪些类别上表现好，在哪些类别上表现差。
• 识别偏见: 发现模型是否对某些类别存在过度的预测或低估。
• 计算更详细的指标: 混淆矩阵是计算精度、召回率、F1分数等指标的基础。

2. 分类报告 (Classification Report)

分类报告是对混淆矩阵指标的进一步提炼和汇总，并以一种易于阅读的格式呈现。它通常包含以下关键指标，并对每个类别提供单独的计算结果，以及对所有类别的宏平均和加权平均。

分类报告中的关键指标:

在深入介绍指标之前，我们先根据混淆矩阵的 TP, FP, FN, TN 定义一些基础的概念：

• 支持度 (Support): 指定类别的实际样本数量。相当于混淆矩阵中该类别在真实标签行或列上的样本总数。

• 精确率 (Precision): 在所有被模型预测为正类的样本中，有多少是真正例。它衡量了模型预测“正类”的准确性，即“预测为正类”的样本中有多少是“真的正类”。

  • 公式: Precision = TP / (TP + FP)
  • 含义: 精确率越高，说明模型对正类的预测越可靠，不那么容易将负类误判为正类。

• 召回率 (Recall): 在所有实际为正类的样本中，有多少被模型正确地预测为正类。它衡量了模型找出所有正类样本的能力，即“为真的正类”中有多少被模型找出来了。也称为 敏感度 或 命中率。

  • 公式: Recall = TP / (TP + FN)
  • 含义: 召回率越高，说明模型越能“抓住”所有正类的样本，不那么容易将正类遗漏。

• F1 分数 (F1-Score): 精确率和召回率的 调和平均值。它综合考虑了精确率和召回率，是在两者都需要关注时的一个折衷指标。当两者都较高时，F1 分数也会很高。

  • 公式: F1-Score = 2 * (Precision * Recall) / (Precision + Recall)
  • 含义: F1 分数越高，说明模型在精确率和召回率之间取得了更好的平衡。

• 准确率 (Accuracy): 在所有样本中，被模型正确分类的样本所占的比例。

  • 公式: Accuracy = (TP + TN) / (TP + TN + FP + FN)
  • 注意: 当类别不平衡时，准确率可能会产生误导。例如，如果 95% 的样本是负类，模型将所有样本都预测为负类，准确率也会高达 95%，但它在预测正类方面毫无作用。

分类报告中的平均值计算:

分类报告通常会提供对所有类别的平均指标，主要有两种方式：

• 宏平均 (Macro Average):

  • 计算方式: 对每个类别的指标 (Precision, Recall, F1-Score) 进行算术平均。
  • 含义: 宏平均对所有类别一视同仁，即使某个类别的支持度很低，它在宏平均中的权重也和其他类别相同。这有助于评估模型在所有类别上的平均性能，尤其适合需要关注所有类别，包括少数类的情况。

• 加权平均 (Weighted Average):

  • 计算方式: 对每个类别的指标 (Precision, Recall, F1-Score) 进行加权平均，权重是该类别的支持度 (Support)。
  • 含义: 加权平均更侧重于样本数量占多数的类别。它反映了模型在整体数据集上的平均性能，更能体现被更多样本代表的类别的表现。

小小的总结一下，我们应该怎么看分类报告？或者说我们应该侧重于哪一些指标?其实有的时候这是视情况而定的。

1. 关注每个类别的指标: 逐个查看每个类别的 Precision, Recall, F1-Score。

   • 高 Precision: 模型预测该类别时，出错的可能性较低。
   • 高 Recall: 模型能较好地找出该类别的所有样本，遗漏较少。
   • 高 F1-Score: 该类别在 Precision 和 Recall 之间取得了较好的平衡。

2. 关注平均指标:

   • Macro Average: 当你需要平等对待所有类别，不希望类别不平衡影响评估时，宏平均是一个好的选择。
   • Weighted Average: 当你更关心模型在整体数据集上的表现，尤其是样本量较大的类别时，加权平均更有参考价值。

3. 结合业务场景: 不同的应用场景对 Precision 和 Recall 的要求可能不同。

   • 例如: 在医疗诊断中，召回率 (Recall) 可能更重要，因为漏诊 (FN) 的代价可能非常高。即使因此产生一些假阳性 (FP) (误诊)，后续的复查也可以纠正。
   • 例如: 在垃圾邮件过滤中，精确率 (Precision) 可能更重要，因为将正常邮件误判为垃圾邮件 (FP) 的代价是用户可能错过重要的信息，而将少量垃圾邮件漏掉 (FN) 的影响相对较小。

混淆矩阵提供了分类结果的原始数据，是理解模型性能的基石。分类报告则是在混淆矩阵的基础上，计算出了一系列更具可解释性的指标，并提供了宏平均和加权平均，使得我们能够从不同维度全面地评估分类模型的性能，并根据具体的业务需求做出合理的判断和选择。

ok,我们回到正题，这是我们拿到的结果：

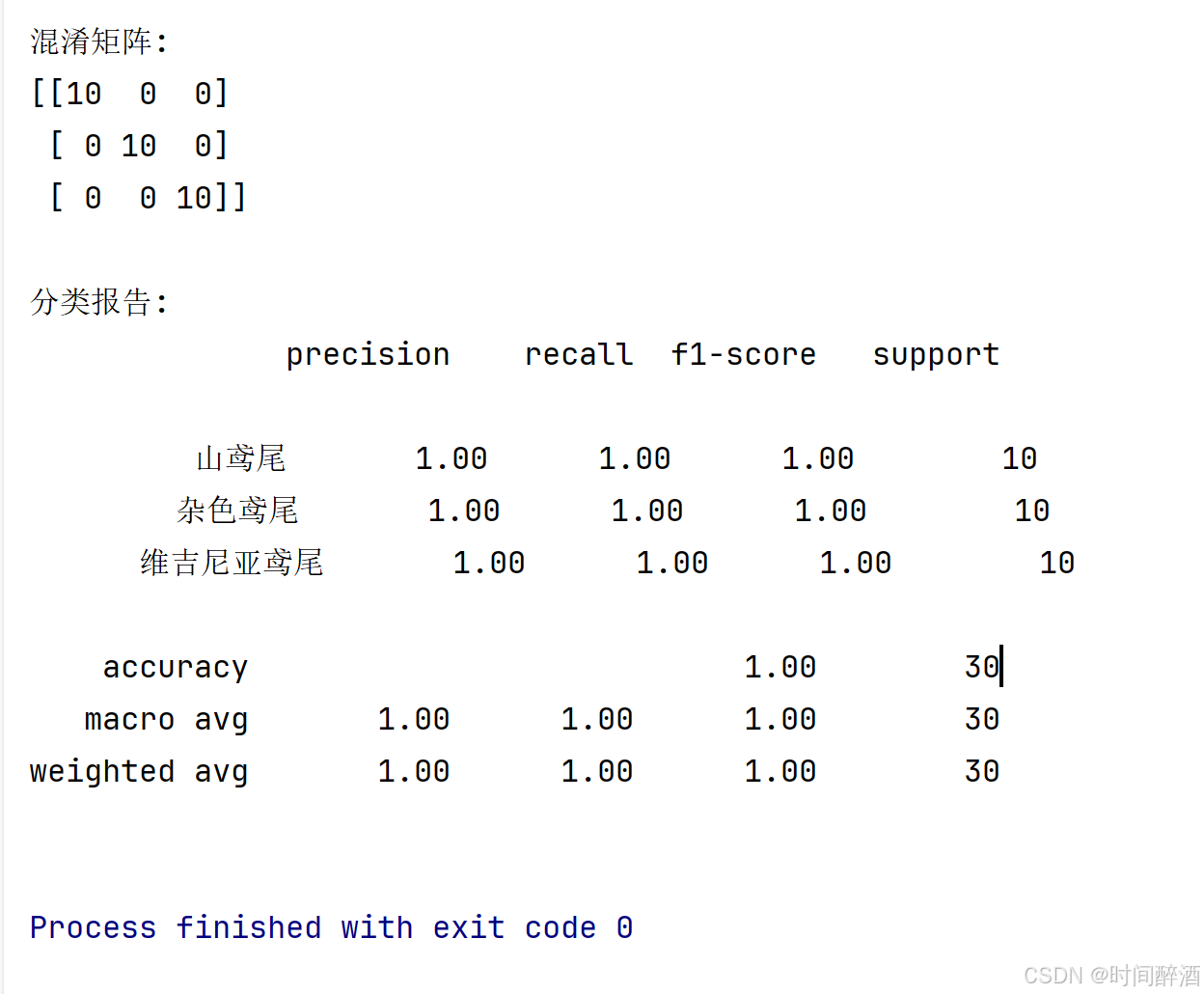
不难发现，精确度是1，很多指标都是1。那么这是不是意味着我们的模型是完美的呢？在实际的机器学习应用中，遇到这种"完美结果"时我们反而需要保持警惕。

这种情况通常暗示着两种可能性：

1. 数据泄露（Data Leakage）
这是指测试集的信息意外地混入了训练过程，导致模型在训练时就已经"见过"了本应在测试阶段才能接触的数据。就像是考试前就拿到了考题的答案，这样的高分自然缺乏说服力。

2. 数据集过于简单
当前使用的教学数据集可能经过精心设计，特征与目标变量之间的关系过于明显，或者特征工程已经完美地捕捉了所有判别信息。然而在真实世界中，数据往往包含噪声、缺失值和不平衡的类别分布，很难达到这种理想状态。

总结：

1. 逻辑回归模型构建

• 使用LogisticRegression类创建模型实例

• random_state参数确保实验结果可复现

• fit()方法进行模型训练，predict()方法进行预测

2. 全面评估指标体系

• 准确率：整体分类正确率，但在类别不平衡时可能失真

• 混淆矩阵：直观展示各类别的预测情况（TP/TN/FP/FN）

• 分类报告：提供精确率、召回率、F1-score等详细指标

• 宏平均 vs 加权平均：针对不同业务场景选择合适的评估视角

3. 遇到完美结果的批判性思维

• 准确率1.0在真实项目中往往是警示信号而非成功标志

• 主要原因：数据泄露或数据集过于简化

• 需要进一步验证而非直接接受表面结果

由于当前使用的是为教学目的简化的数据集，我们暂时不深入探讨复杂的数据验证技术。在后续课程中，当我们接触到更复杂的真实世界数据集和高级模型时，我会详细讲解：

• 如何系统性地检查数据泄露

• 交叉验证的深入应用与实践技巧

• 学习曲线和验证曲线的分析方法

• 特征重要性和模型可解释性工具的使用

现在，让我们先聚焦于理解基础概念，为后续更复杂的学习打下坚实基础。接下来，我们将用更复杂的数据集和模型探讨即使面对"完美"结果，如何从中提取价值。

作者本人水平有限，非常欢迎任何反馈和指正，请随时指出我可能存在的误解、遗漏或表述不当之处。

我将继续深入学习机器学习和统计学领域，并持续更新我的理解和最佳实践。我愿意虚心接受反馈，不断打磨和完善我的内容，以便为读者提供更可靠、更有价值的信息。

感谢您提供的建议，它们对我至关重要！