当前位置：首页 > news >正文

【算法】【优选算法】BFS 解决边权相同最短路问题

news 2025/9/24 8:01:55

一、1926.迷宫中离⼊⼝最近的出⼝

题目链接：1926.迷宫中离⼊⼝最近的出⼝

题目描述：

题目解析：

给我们一个字符数组 + 表示墙，. 表示路。
求给我们的起始坐标，上下左右走到边界最短的距离。
没路出去返回-1，刚开始的起点不算距离。

解题思路：

使用层序遍历，从给我们的起点开始，
每一次都将队列中的元素全部取出，相当于进了一步。
直到没路可走，或者走到边界。
使用一个相同大小的标记数组，将走过的路和墙标记。标记过的下标不入队。
解题代码：

时间复杂度：O(M*N)
空间复杂度：O(M*N)
class Solution {int[] dx = {1,-1,0,0};int[] dy = {0,0,1,-1};boolean[][] flag;int m, n;public int nearestExit(char[][] maze, int[] entrance) {m = maze.length;n = maze[0].length;flag = new boolean[m][n];for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {if(maze[i][j] == '+' ) {flag[i][j] = true;}}}Queue<int[]> queue = new LinkedList<>();queue.add(new int[]{entrance[0], entrance[1]});flag[entrance[0]][entrance[1]] = true;int length = 0;while(!queue.isEmpty()) {length++;int size = queue.size();//将这一层元素出完for(int i = 0; i < size; i++) {int[] arr = queue.poll();//层序遍历入队for(int j = 0; j < 4; j++) {int x = dx[j] + arr[0];int y = dy[j] + arr[1];if( x >= 0 && x < m&& y >= 0 && y < n&& maze[x][y] == '.' && !flag[x][y]) {//结束条件if(x == 0 || x == m - 1 || y == 0 || y == n - 1) {return length;}System.out.println(x +" "+y +" 入队"+length);queue.add(new int[]{x,y});flag[x][y] = true;}}}}return - 1;}
}

二、433. 最⼩基因变化

题目链接：433. 最⼩基因变化

题目描述：

题目解析：

给我们一个起始字符串start和最终字符串end，长度固定为8
起始字符串每一次可以变化一个字符，并且变化后的字符串必须属于bank字符串数组中的值
求最短从start变成end的次数。

解题思路：

我们将起始的字符串中的字符，每一个字符都有四个突变选择，层序遍历每一种突变的可能，符合条件（包含在基因库，突变过后是全新未突变过得到的），直到与最后end相同为止。
我们需要使用两个hash表，一个记录每个符合条件的突变结果，一个记录基因库好实行对比。
我们顺序遍历起始字符串，每一次队列中的元素，相当于突变一次可以达到的结果，每次将队列中的元素出完，出一次就相当于进行一次实际突变。
当最终的end字符串不在基因库，或者进行突变完了（队列空了），还没有找到结果，就返回-1。
解题代码：

//时间复杂度：O(N)
//空间复杂度：O(N)
class Solution {public int minMutation(String startGene, String endGene, String[] bank) {Set<String> flag = new HashSet<>();//标记改变过的基因Set<String> hash = new HashSet<>();//记录基因库bank元素for(String s : bank) hash.add(s);System.out.println(hash.toString());//end基因无效if(!hash.contains(endGene)) return -1;Queue<String> queue = new LinkedList<>();queue.add(startGene);flag.add(startGene);int length = 0;char[] change = {'A','C','G','T'};while(!queue.isEmpty()) {int size = queue.size();length++;//层序遍历for(int i = 0; i < size; i++) {String t = queue.poll();//遍历字符串的字符，一一突变for(int j = 0; j < 8; j++) {char[] tmp = t.toCharArray();//突变for(int k = 0; k < 4; k++) {tmp[j] =  change[k];String next = new String(tmp);//入队条件if(hash.contains(next) && !flag.contains(next)) {queue.add(next);flag.add(next);}//结束条件if(next.equals(endGene)) return length;}}}}return -1;}
}

三、127. 单词接⻰

题目链接：127. 单词接⻰

题目描述：

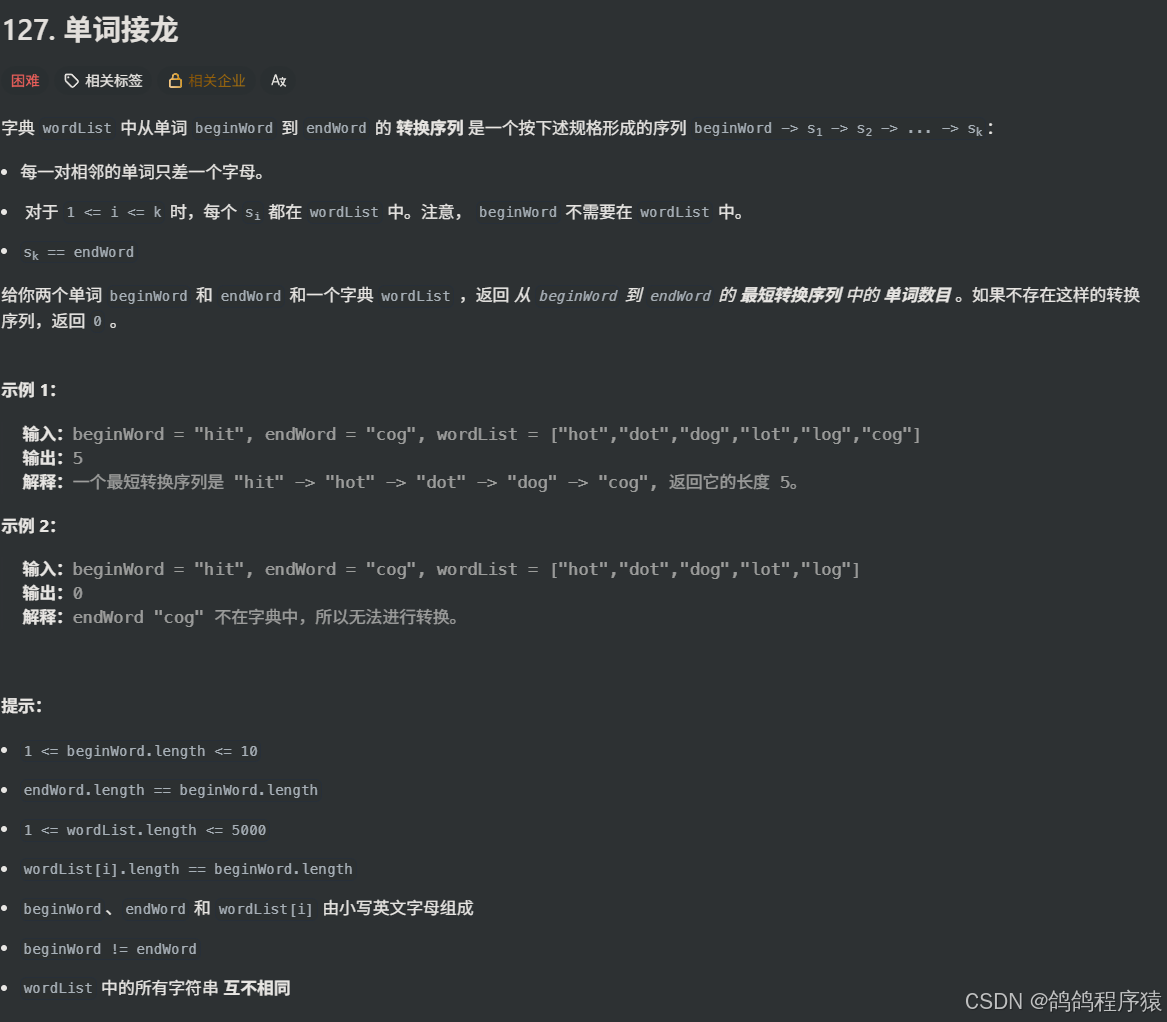
题目解析：

给我们一个起始单词beginWord和一个结束单词endWord，和一个字典wordList
我们一次变化一个字母，使beginWord 变到 endWord，并且每一次变化后单词必须在 wordList 中

解题思路：

跟上一题一模一样，只不过变化是26个小写字母
解题代码：

//时间复杂度：O(N)
//空间复杂度：O(N)
class Solution {public int ladderLength(String beginWord, String endWord, List<String> wordList) {Set<String> hash = new HashSet<>();for(String s : wordList) hash.add(s);//endWord不在字典if(!hash.contains(endWord)) return 0;//标记表Set<String> flag = new HashSet<>();flag.add(beginWord);//队列Queue<String> queue = new LinkedList<>();queue.add(beginWord);int ret = 1;while(!queue.isEmpty()) {int size = queue.size();ret++;for(int k = 0; k < size; k++) {String s = queue.poll();for(int i = 0; i < s.length(); i++) {char[] tmp = s.toCharArray();//26个字母for(char j = 'a'; j <= 'z'; j++) {tmp[i] = j;//入队条件String string = new String(tmp);if(hash.contains(string) && !flag.contains(string)) {System.out.println(string);queue.add(string);flag.add(string);}//结束条件if(string.equals(endWord)) return ret;}}}}return 0;}
}

四、675. 为⾼尔夫⽐赛砍树

题目链接：675. 为⾼尔夫⽐赛砍树

题目描述：

题目解析：

给我们一个数组，让我们从根据数组值的大小依次砍树，0代表墙，1代表地面
让我们计算一次砍树，我们需要走的最短路径

解题思路：

我们先将怎么砍树记录出来，将数组中大于0的值，按数组值从小到大排序，将他们的下标存入一个数组中；
然后该数组中每一个前面元素（起始）到后元素（结尾）都相当于求一次最短路径
注意第一次是坐标（0,0）起始，因此当第二个坐标是代表地面的时候，我们就要跳过这一次。例如：[[1,2,3],[0,0,4],[7,6,5]]这个数组。

解题代码：

//时间复杂度：O(N)
//空间复杂度：O(N)
class Solution {int[] dx = {1,-1,0,0};int[] dy = {0,0,1,-1};int m, n;public int cutOffTree(List<List<Integer>> forest) {m = forest.size();n = forest.get(0).size();//找出砍树的顺序，根据树的大小排序List<int[]> trees = new ArrayList<>();for(int i = 0; i < m; i++) {for(int j = 0; j < n; j++) {if(forest.get(i).get(j) > 0) trees.add(new int[]{i,j});}}//排序Collections.sort(trees, (a,b) -> {return forest.get(a[0]).get(a[1]) - forest.get(b[0]).get(b[1]);});int ret = 0; int beginX = 0;int beginY = 0;//标记数组for(int[] tree : trees) {int endX = tree[0];int endY = tree[1];int tep = 0;//下一步是地面if(forest.get(endX).get(endY) == 1) continue;tep = bfs(forest,beginX,beginY,endX,endY);if(tep == -1) return -1;ret += tep;beginX = endX;beginY = endY;}return ret;}//ab代表下一棵砍的坐标，xy表示当前的位置public int bfs(List<List<Integer>> forest, int beginX, int beginY, int endX, int endY) {//当前就是要砍的树if((beginX == endX && beginY == endY)) return 0;//标记数组，走过的路boolean[][] flag = new boolean[m][n];int tep = 0;Queue<int[]> queue = new LinkedList<>();queue.add(new int[]{beginX,beginY});flag[beginX][beginY] = true;//bfswhile(!queue.isEmpty()) {int size = queue.size();tep++;while(size -- != 0) {int[] arr = queue.poll();int nx,ny;for(int i = 0; i < 4; i++) {nx = arr[0] + dx[i];ny = arr[1] + dy[i];//入队条件if(nx >= 0 && nx < m&& ny >= 0 && ny < n&& !flag[nx][ny]&& forest.get(nx).get(ny) != 0) {queue.add(new int[]{nx,ny});flag[nx][ny] = true;//到了if(nx == endX && ny == endY) return tep;}}}}return -1;}
}