当前位置：首页 > news >正文

一维卡尔曼滤波（无过程噪声）详解

news 2025/9/24 6:53:26

卡尔曼滤波是一种最优线性滤波器，用于从含噪声的测量中估计系统状态。本文聚焦于一维且不带过程噪声的卡尔曼滤波，解析其核心原理与公式推导。

一、状态预测：从当前状态外推未来状态

卡尔曼滤波的 “预测” 阶段包含状态外推和协方差外推（估计不确定性外推），两者均由系统的动态模型决定。

1. 状态外推（State Extrapolation）

状态外推是利用系统动态模型，从 “当前状态估计” 推导 “下一时刻先验状态估计”。

例子 1：系统状态恒定（如金条重量测量）

若系统状态（如金条重量）不随时间变化，动态模型为 “恒定”，则状态外推公式为： $\hat{x}_{n+1,n} = \hat{x}_{n,n}$ 其中：

$\hat{x}_{n,n}$ ：第 n 时刻后验状态估计（结合测量后的最优估计）。
$\hat{x}_{n+1,n}$ ：第 $n+1$ 时刻先验状态估计（仅由动态模型外推的估计）。

例子 2：一维运动模型（如雷达跟踪位置与速度）

若系统是 “位置 - 速度” 的一维运动（速度恒定），动态模型为：

$\begin{cases} \hat{x}_{n+1,n} = \hat{x}_{n,n} + \Delta t \cdot \hat{\dot{x}}_{n,n} \\ \hat{\dot{x}}_{n+1,n} = \hat{\dot{x}}_{n,n} \end{cases}$

其中：

$\hat{x}$ ：位置的状态估计， $\hat{\dot{x}}$ ：速度的状态估计。
$\Delta t$ ：时间步长，速度假设恒定（因此 $\hat{\dot{x}}_{n+1,n} = \hat{\dot{x}}_{n,n}$ ），位置由“当前位置 + 速度×时间”更新。

2. 协方差外推（Covariance Extrapolation）

“协方差”描述状态估计的不确定性（方差）。协方差外推是从“当前状态的不确定性”推导“下一时刻先验状态的不确定性”。

例子1：系统状态恒定

由于状态无变化，不确定性也不传播，因此协方差外推公式为：

$\hat{p}_{n+1,n} = \hat{p}_{n,n}$

其中 $p$ 表示状态估计的方差（不确定性）。

例子2：一维运动模型（位置-速度）

位置的不确定性会因速度的不确定性而传播，由 $x = x_0 + v\Delta t$ ，方差满足 $V(x) = V(x_0) + \Delta t^2 V(v)$ ，而速度不确定性恒定。因此协方差外推公式为：

$\begin{cases} p^x_{n+1,n} = p^x_{n,n} + \Delta t^2 \cdot p^v_{n,n} \\ p^v_{n+1,n} = p^v_{n,n} \end{cases}$

其中：

$p^x$ ：位置估计的方差（不确定性）。
$p^v$ ：速度估计的方差（不确定性）。

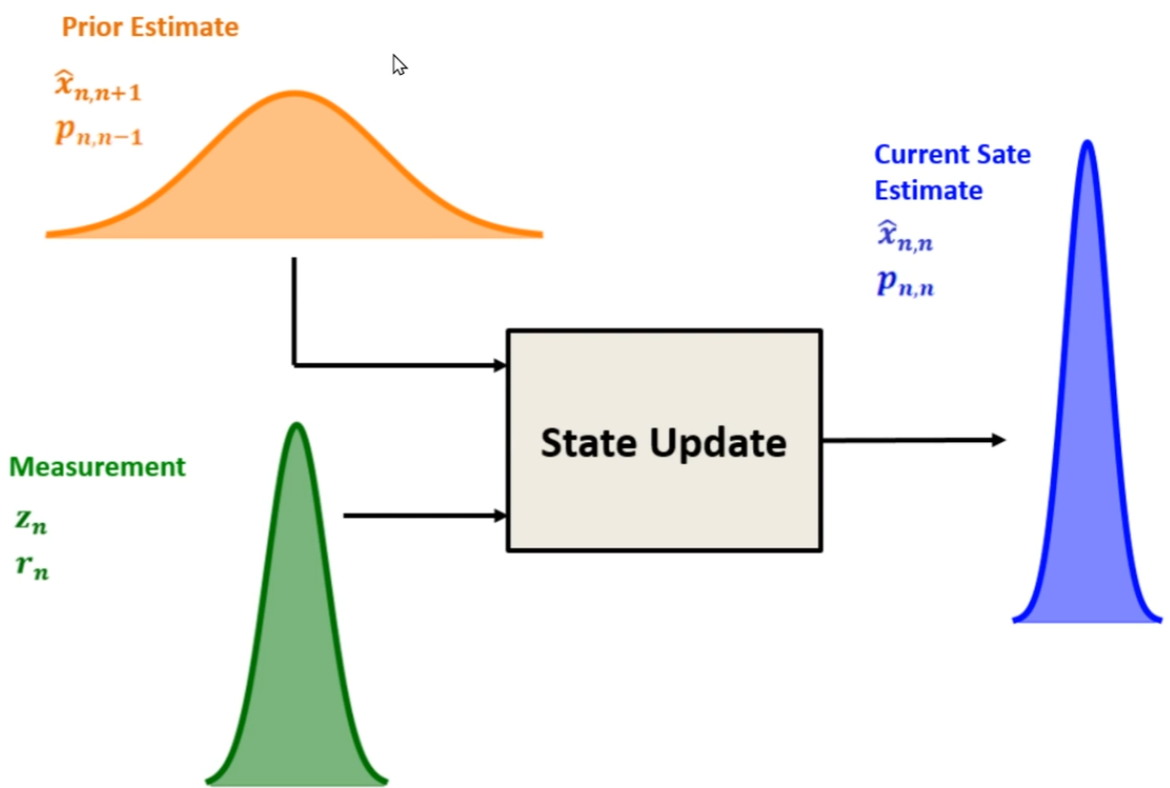
二、状态更新：结合测量优化估计

“更新”阶段通过结合先验状态估计和当前测量，得到“后验状态估计”（更优的状态估计），同时更新不确定性（协方差）。

1. 状态更新的思想：加权平均最小化方差

当前状态估计是“先验状态估计”和“测量值”的加权平均：

$\hat{x}_{n,n} = w_1 z_n + (1 - w_1) \hat{x}_{n,n-1}$

其中：

$z_n$ ：第 $n$ 时刻的测量值。
$\hat{x}_{n,n-1}$ ：第 $n$ 时刻的先验状态估计（由预测阶段得到）。
$w_1$ ：测量值的权重， $1 - w_1$ ：先验估计的权重。

我们的目标是最小化当前状态估计的方差 $p_{n,n}$ 。根据方差的性质（若随机变量 ( X ) 的方差为 $\sigma^2$ ，则 $kX$ 的方差为 $k^2 \sigma^2$ ；独立变量和的方差为方差和），当前状态估计的方差为：

$p_{n,n} = w_1^2 r_n + (1 - w_1)^2 p_{n,n-1}$

其中：

$r_n$ ：测量值 $z_n$ 的方差（测量不确定性）。
$p_{n,n-1}$ ：先验状态估计 $\hat{x}_{n,n-1}$ 的方差（先验不确定性）。

2. 卡尔曼增益：最优权重的推导

为了最小化 $p_{n,n}$ ，对 $p_{n,n}$ 关于 $w_1$ 求偏导并令导数为0：

$\frac{d p_{n,n}}{d w_1} = 2 w_1 r_n - 2 (1 - w_1) p_{n,n-1} = 0$

解得最优权重：

$w_1 = \frac{p_{n,n-1}}{p_{n,n-1} + r_n}$

这个最优权重就是卡尔曼增益 ( $K_n$ )，因此卡尔曼增益公式为：

$K_n = \frac{p_{n,n-1}}{p_{n,n-1} + r_n}$

卡尔曼增益 ( $K_n$ ) 满足 ( $0 \leq K_n \leq 1$ )：

若测量不确定性 ( $r_n$ ) 小（测量准确），则 ( $K_n$ ) 大（更信任测量）。
若先验不确定性 ( $p_{n,n-1}$ ) 小（先验估计准确），则 ( $K_n$ ) 小（更信任先验）。

3. 状态更新公式

将卡尔曼增益 $K_n$ 代入“加权平均”的状态估计公式，得到更简洁的形式：

$\hat{x}_{n,n} = \hat{x}_{n,n-1} + K_n \left( z_n - \hat{x}_{n,n-1} \right)$

其中 $z_n - \hat{x}_{n,n-1}$ 称为创新（Innovation），表示“测量与先验估计的差异”，卡尔曼增益决定了“创新”对状态更新的贡献程度。

4. 协方差更新公式

将 $K_n = \frac{p_{n,n-1}}{p_{n,n-1} + r_n}$ 代入方差公式 $p_{n,n} = w_1^2 r_n + (1 - w_1)^2 p_{n,n-1}$ ，经过化简（展开、合并同类项）可得：

$p_{n,n} = (1 - K_n) p_{n,n-1}$

该公式表明：更新后的状态不确定性（方差）是“先验不确定性”乘以 $(1 - K_n)$ 。由于 ( $0 \leq K_n \leq 1$ )，因此 ( $p_{n,n} \leq p_{n,n-1}$ )，即估计的不确定性随滤波迭代逐渐减小。

三、总结：一维无过程噪声卡尔曼滤波的流程

一维无过程噪声的卡尔曼滤波分为预测和更新两个核心阶段：

预测阶段：
- 状态外推：用系统动态模型，从当前后验状态估计外推下一时刻先验状态估计（如 ( $\hat{x}_{n+1,n} = \hat{x}_{n,n}$ ) 或 ( $\hat{x}_{n+1,n} = \hat{x}_{n,n} + \Delta t \hat{\dot{x}}_{n,n}$ )）。
- 协方差外推：用动态模型传播不确定性（如 $p_{n+1,n} = p_{n,n}$ 或 $p^x_{n+1,n} = p^x_{n,n} + \Delta t^2 p^v_{n,n}$ ）。
更新阶段：
- 计算卡尔曼增益 $K_n = \frac{p_{n,n-1}}{p_{n,n-1} + r_n}$ ，确定测量与先验估计的权重。
- 状态更新：结合先验估计和测量，得到后验状态估计 $\hat{x}{n,n} = \hat{x}{n,n-1} + K_n (z_n - \hat{x}_{n,n-1})$ 。
- 协方差更新：更新后验不确定性 $p_{n,n} = (1 - K_n) p_{n,n-1}$ 。