磁共振成像原理(理论)11:梯度回波 (Gradient Echoes)
磁共振成像中常用的另一种回波信号形式是通过时变梯度磁场产生的。此类回波称为梯度回波,以区别于自旋回波或受激回波。梯度回波形成的核心概念在于:梯度场能够以可控方式使信号失相位和重相位,从而产生一个或多个回波信号。为理解这一机制,我们首先正式定义梯度场。
梯度场 (Gradient Field)
在磁共振成像中,梯度场 B⃗G\vec{B}_{G}BG 是一种特殊的不均匀场,其zzz分量沿特定方向(称为梯度方向)呈线性变化。若满足:
BG,z=Gxx(4.59) B_{G,z} = G_{x}x \tag {4.59} BG,z=Gxx(4.59)
则 B⃗G\vec{B}_{G}BG 称为 xxx 梯度场,其中 GxG_xGx 称为xxx梯度。在xxx梯度Gx>0G_x>0Gx>0指的是,沿着x+x+x+方向移动,磁场强度的大小在递增,但是磁场强度的方向一直是沿着zzz方向的(k⃗\vec kk)。
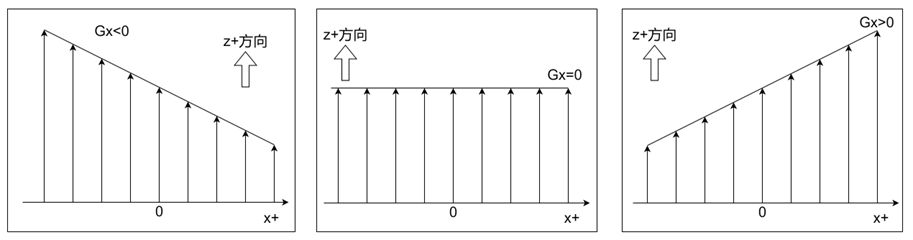
梯度场的理解是初学者经常犯的一个错误,以为xxx梯度是产生了xxx方向的磁场分量,为了更好的说明这一点,如下图所示:
- 下图左:当Gx=−1<0G_x=-1<0Gx=−1<0时,在x=0x=0x=0处的磁场强度是(B0+Gx0)k⃗=B0k⃗(B_0+G_x0)\vec k=B_0\vec k(B0+Gx0)k=B0k,在x=+1x=+1x=+1处的磁场强度是(B0+Gx1)k⃗=(B0−1)k⃗(B_0+G_x1)\vec k=(B_0-1)\vec k(B0+Gx1)k=(B0−1)k,在x=−1x=-1x=−1处的磁场强度是(B0−Gx1)k⃗=(B0+1)k⃗(B_0-G_x1)\vec k=(B_0+1)\vec k(B0−Gx1)k=(B0+1)k
- 下图中:当Gx=0G_x=0Gx=0时,在x=0x=0x=0处的磁场强度是(B0+Gx0)k⃗=B0k⃗(B_0+G_x0)\vec k=B_0\vec k(B0+Gx0)k=B0k,在x=+1x=+1x=+1处的磁场强度是(B0+Gx1)k⃗=B0k⃗(B_0+G_x1)\vec k=B_0\vec k(B0+Gx1)k=B0k,在x=−1x=-1x=−1处的磁场强度是(B0−Gx0)k⃗=B0k⃗(B_0-G_x0)\vec k=B_0\vec k(B0−Gx0)k=B0k
- 下图右:当Gx=1>0G_x=1>0Gx=1>0时,在x=0x=0x=0处的磁场强度是(B0+Gx0)k⃗=B0k⃗(B_0+G_x0)\vec k=B_0\vec k(B0+Gx0)k=B0k,在x=+1x=+1x=+1处的磁场强度是(B0+Gx1)k⃗=(B0+1)k⃗(B_0+G_x1)\vec k=(B_0+1)\vec k(B0+Gx1)k=(B0+1)k,在x=−1x=-1x=−1处的磁场强度是(B0−Gx1)k⃗=(B0−1)k⃗(B_0-G_x1)\vec k=(B_0-1)\vec k(B0−Gx1)k=(B0−1)k
所以GxG_xGx是沿着xxx方向每移动1m所引起的zzz方向磁场大小的增量。因此越偏离xxx中心,受到的影响也越大。如果GxG_xGx是一个常数,此时磁场沿着xxx方向线性分布。
类似地,若满足:
BG,z=Gyy(4.60) B_{G,z} = G_{y}y \tag {4.60} BG,z=Gyy(4.60)
则称为yyy梯度场。若满足:
BG,z=Gzz(4.61) B_{G,z} = G_{z}z \tag {4.61} BG,z=Gzz(4.61)
则称为zzz梯度场。
梯度系统由三个独立的梯度线圈(xxx、yyy、zzz 梯度线圈)组成,理想情况下各产生一个方向的梯度场。需注意:每个梯度线圈产生的磁场也存在xxx分量(BG,xB_{G,x}BG,x)和yyy分量(BG,yB_{G,y}BG,y),但由于主磁场 B⃗0\vec{B}_0B0 在zzz方向极强,这些分量常被忽略。因此,BG,zB_{G,z}BG,z本身常被简称为“梯度场”,且 BG,zB_{G,z}BG,z 与 B⃗G\vec{B}_GBG 在无歧义时可互换使用。注:根据麦克斯韦方程组,此类梯度场并不严格存在,但在 MRI 理论中作为理想模型使用。
因此感兴趣区域内的总磁场可表示为:
B⃗=(B0+BG,z)k⃗(4.62) \vec{B} = (B_0 + B_{G,z})\vec{k} \tag {4.62} B=(B0+BG,z)k(4.62)
其中 BG,zB_{G,z}BG,z 的定义见公式 (4.59)-(4.61)。若所有梯度线圈同时开启,则:
BG,z=Gxx+Gyy+Gzz(4.63) B_{G,z} = G_x x + G_y y + G_z z \tag {4.63} BG,z=Gxx+Gyy+Gzz(4.63)
进而总磁场为(注意都是zzz方向的分量):
B⃗=(B0+Gxx+Gyy+Gzz)k⃗(4.64) \vec{B} = (B_0 + G_x x + G_y y + G_z z)\vec{k} \tag {4.64} B=(B0+Gxx+Gyy+Gzz)k(4.64)
将三个梯度组合为梯度矢量 G⃗\vec{G}G:
G⃗=(Gx,Gy,Gz)=Gxi⃗+Gyj⃗+Gzk⃗(4.65) \vec{G} = (G_x, G_y, G_z) = G_x \vec{i} + G_y \vec{j} + G_z \vec{k} \tag {4.65} G=(Gx,Gy,Gz)=Gxi+Gyj+Gzk(4.65)
G⃗\vec{G}G 的方向称为梯度场 B⃗G\vec{B}_GBG 或 B⃗\vec{B}B 的梯度方向。此时公式 (4.63) 可改写为:
BG,z=G⃗⋅r⃗(4.66) B_{G,z} = \vec{G} \cdot \vec{r} \tag {4.66} BG,z=G⋅r(4.66)
其中 r⃗=(x,y,z)\vec{r} = (x, y, z)r=(x,y,z) 为位置矢量。
需区分 BG,zB_{G,z}BG,z 的梯度方向与梯度场本身的方向:虽然通过控制 GxG_xGx、GyG_yGy、GzG_zGz 可使 G⃗\vec{G}G 指向任意方向,但 B⃗G\vec{B}_GBG 的方向通常未知且无关紧要。
若 G⃗\vec{G}G 在特定时间间隔内为常数,则称为静态梯度场;否则为时变梯度场。两者均广泛应用于 MRI 中。
梯度回波的形成
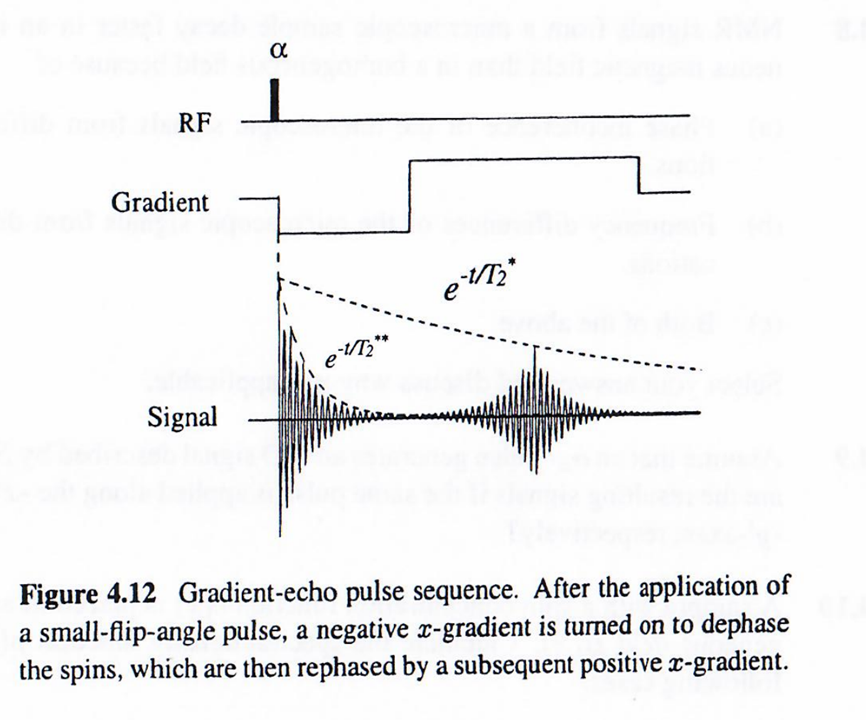
如上图脉冲序列为例:施加α\alphaα角射频脉冲(小角度激发常用于快速成像)后,开启负xxx梯度。位于不同xxx位置的自旋将积累不同相位(在旋转坐标系下):
ϕ(x,t)=γ∫0t(−Gxx)dt=−γGxxt(0≤t≤τ)(4.67) \phi(x, t) = \gamma \int_0^t (-G_x x) dt = -\gamma G_x x t \qquad (0 \leq t \leq \tau) \tag {4.67} ϕ(x,t)=γ∫0t(−Gxx)dt=−γGxxt(0≤t≤τ)(4.67)
该式表明:激发脉冲后,自旋相位一致性随时间逐渐恶化,信号衰减时间常数为 T2∗∗T_2^{**}T2∗∗。当 t>3T2∗∗t > 3T_2^{**}t>3T2∗∗ 时信号衰减为零。若在此时施加相同强度的正梯度,横向磁化分量将逐渐重相位,信号重新增长。
在 t≥τt \geq \taut≥τ 时段,自旋相位角变为:
ϕ(x,t)=γ∫0τ(−Gxx)dt+∫τtGxxdt^=−γGxxτ+γ∫τtGxxdt^=−γGxxτ+γGxx(t−τ)(τ≤t≤2τ)(4.68) \begin{align*}
\phi(x, t) &=\gamma \int_0^\tau (-G_x x) dt + \int_{\tau}^t G_x x d\hat{t}\\
&= -\gamma G_x x \tau + \gamma \int_{\tau}^t G_x x d\hat{t} \\
&= -\gamma G_x x \tau + \gamma G_x x (t - \tau) \qquad (\tau \leq t \leq 2\tau)
\end{align*} \tag {4.68} ϕ(x,t)=γ∫0τ(−Gxx)dt+∫τtGxxdt^=−γGxxτ+γ∫τtGxxdt^=−γGxxτ+γGxx(t−τ)(τ≤t≤2τ)(4.68)
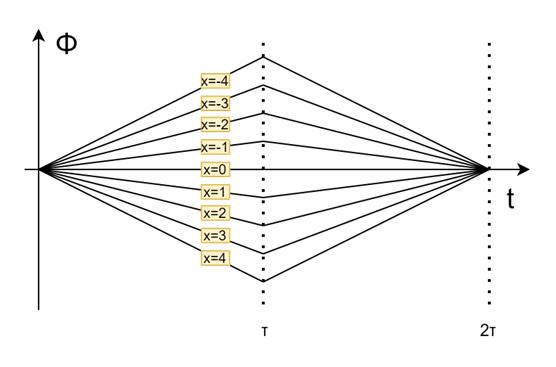
下图是相位演化:
在0<t<=τ0<t<=\tau0<t<=τ时,位于不同xxx位置的自旋将积累不同相位(在旋转坐标系下)进而导致失相,该失相使得信号以T2∗∗T_2^{**}T2∗∗衰减。在t=τt=\taut=τ时相位分散达到最大。
在τ<t<2τ\tau<t<2\tauτ<t<2τ时,负梯度引入的相位分散在正梯度开启后逐渐减小。经过时间 τ\tauτ 后(t=2τt=2\taut=2τ),所有xxx位置的自旋相位归零(ϕ=0\phi=0ϕ=0),即完全重相位,形成回波信号。此分析可推广至去相位与重相位梯度强度不等的情况,此时回波时间不一定等于 2τ2\tau2τ。
若 B⃗0\vec{B}_0B0 场不均匀,梯度反转无法使自旋完全重相位。因此,梯度回波的幅度携带 T2∗T_2^*T2∗ 权重(而非 T2T_2T2 权重),这是梯度回波与射频回波的关键差异之一。下面是射频回波:
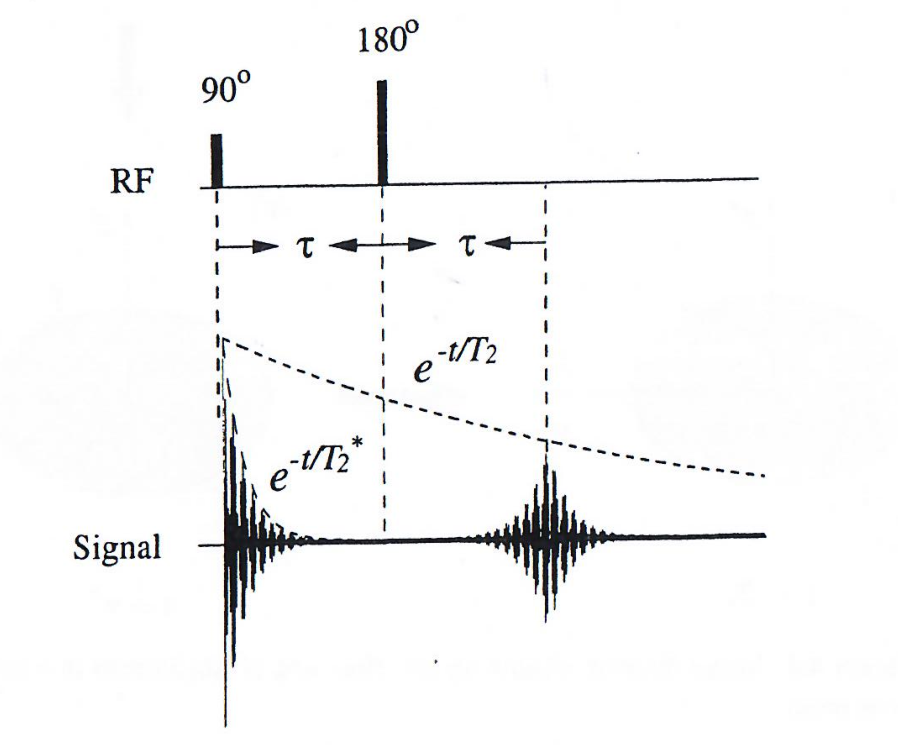
在t=0t=0t=0时刻激发90°90 \degree90°脉冲。因为B0B_0B0不均匀(但是不随时间变化)导致空间r处的原子团的自旋进动频率为:
Δω(r⃗)=γΔB0(r⃗)\Delta\omega(\vec r) = \gamma \Delta B_0(\vec r)Δω(r)=γΔB0(r)
这也进而使得不同原子团之间的相位失去同步(失相)的速度加剧(相比微观磁场环境因为相邻原子核自旋导致的磁场涨落而导致的T2T_2T2衰减),最终导致信号以时间常数T2∗T_2^*T2∗衰减:
1T2∗=1T2+γΔB0 \frac{1}{T_2^*} = \frac{1}{T_2} + \gamma \Delta B_0 T2∗1=T21+γΔB0
当t>0t>0t>0时刻,空间r处原子团累积的相位差为
Δϕ(t,r⃗)=γΔB0(r⃗)t\Delta\phi(t,\vec r) = \gamma \Delta B_0(\vec r) tΔϕ(t,r)=γΔB0(r)t
在t=τ−t=\tau_-t=τ−时刻,空间r处原子团累积的相位差为
Δϕ(τ−,r⃗)=γΔB0(r⃗)τ\Delta\phi(\tau_-,\vec r) = \gamma \Delta B_0(\vec r) \tauΔϕ(τ−,r)=γΔB0(r)τ
在t=τ+t=\tau_+t=τ+时刻,空间r处原子团累积的相位差因为180°180 \degree180°脉冲发生反转
Δϕ(τ+,r⃗)=−γΔB0(r⃗)τ\Delta\phi(\tau_+,\vec r) = -\gamma \Delta B_0(\vec r) \tauΔϕ(τ+,r)=−γΔB0(r)τ
当t>τt>\taut>τ时刻,空间r处原子团累积的相位差为
Δϕ(t,r⃗)=−γΔB0(r⃗)τ+γΔB0(r⃗)(t−τ)\Delta\phi(t,\vec r) = -\gamma \Delta B_0(\vec r) \tau + \gamma \Delta B_0(\vec r) (t-\tau)Δϕ(t,r)=−γΔB0(r)τ+γΔB0(r)(t−τ)
当t=2τt=2\taut=2τ时,空间r处原子团累积的相位差回到0。实际上空间中任意r处原子团累积的相位差都回到了0,B0B_0B0不均匀的失相被重新聚相,此时射频回波产生。
回到梯度回波,在t=0t=0t=0时刻激发90°90 \degree90°脉冲。因为B0B_0B0不均匀(但是不随时间变化)和人为施加的xxx负梯度场(这里假设是x方向,为了下面符号方便),他们共同作用导致空间r处的原子团的自旋进动频率为:
Δω(r⃗)=γ[ΔB0(r⃗)−Gxx]\Delta\omega(\vec r) = \gamma [\Delta B_0(\vec r)- G_x x]Δω(r)=γ[ΔB0(r)−Gxx]
当t>0t>0t>0时刻,空间r处原子团累积的相位差为
Δϕ(t,r⃗)=γ[ΔB0(r⃗)−Gxx]t\Delta\phi(t,\vec r) = \gamma [\Delta B_0(\vec r)-G_x x] tΔϕ(t,r)=γ[ΔB0(r)−Gxx]t
在t=τt=\taut=τ时刻,开始施加xxx正梯度场(注意这里相位没有反转,而是直接继承)
Δϕ(τ,r⃗)=γ[ΔB0(r⃗)−Gxx]τ\Delta\phi(\tau,\vec r) = \gamma [\Delta B_0(\vec r)- G_x x] \tauΔϕ(τ,r)=γ[ΔB0(r)−Gxx]τ
当t>τt>\taut>τ时刻,空间r处原子团累积的相位差为
Δϕ(t,r⃗)=γ[ΔB0(r⃗)−Gxx]τ+γ[ΔB0(r⃗)+Gxx](t−τ)\Delta\phi(t,\vec r) = \gamma [\Delta B_0(\vec r)- G_x x] \tau + \gamma [\Delta B_0(\vec r)+ G_x x](t-\tau) Δϕ(t,r)=γ[ΔB0(r)−Gxx]τ+γ[ΔB0(r)+Gxx](t−τ)
当t=2τt=2\taut=2τ时刻,空间r处原子团累积的相位差为
Δϕ(2τ,r⃗)=γ[ΔB0(r⃗)−Gxx]τ+γ[ΔB0(r⃗)+Gxx](2τ−τ)=2γΔB0(r⃗)τ\Delta\phi(2\tau,\vec r) = \gamma [\Delta B_0(\vec r)- G_x x] \tau + \gamma [\Delta B_0(\vec r)+ G_x x](2\tau-\tau) = 2\gamma \Delta B_0(\vec r)\tauΔϕ(2τ,r)=γ[ΔB0(r)−Gxx]τ+γ[ΔB0(r)+Gxx](2τ−τ)=2γΔB0(r)τ
所以当t=2τt=2\taut=2τ时,空间r处原子团累积的相位差没有回到0 ,实际上等于2γΔB0(r⃗)τ2\gamma \Delta B_0(\vec r)\tau2γΔB0(r)τ,所以B0B_0B0不均匀导致的相位发散并没有被重新聚相,但是梯度场导致的相位累积在t=2τt=2\taut=2τ被恢复了,此时梯度回波产生。
总结:
- 射频回波以T2∗T_2^{*}T2∗进行衰减和恢复,回波的峰值和初始值有e−TET2e^{\frac{-T_E}{T_2^{}}}eT2−TE进行衰减。
- 梯度回波以T2∗∗T_2^{**}T2∗∗进行衰减和恢复,回波的峰值和初始值仍以e−TET2∗e^{\frac{-T_E}{T_2^{*}}}eT2∗−TE进行衰减
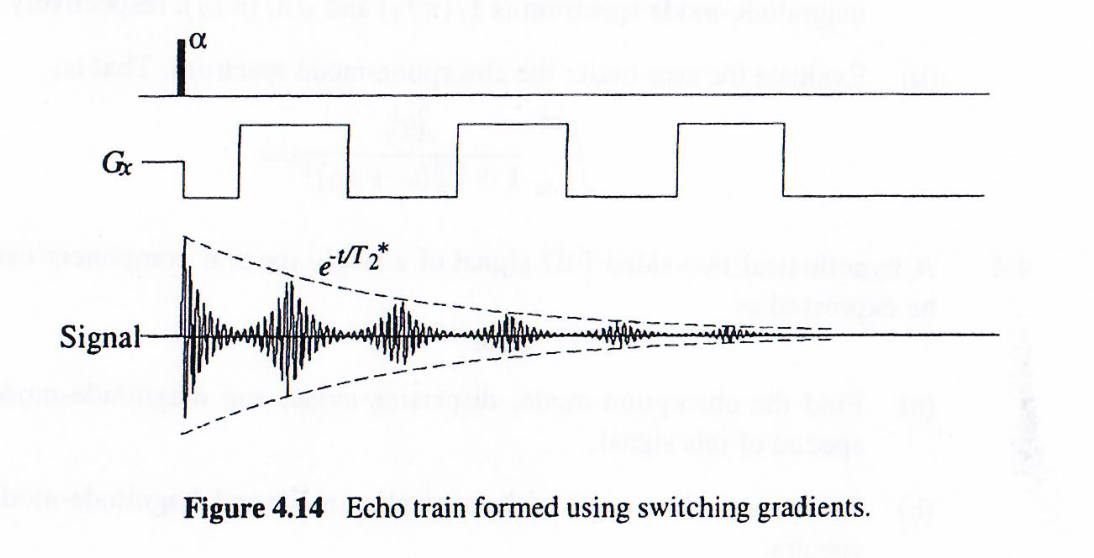
因为T2∗∗<T2∗T_2^{**}<T_2^{*}T2∗∗<T2∗,所以梯度回波的TET_ETE远小于射频回波的TET_ETE,使得梯度回波可以更快的完成成像。下图演示了,利用一个射频α\alphaα脉冲,仅操控梯度场即可实现多个回波。但是越靠后的回波幅值越小。