[学习笔记][机器学习-周志华] 第1章 绪论

1.1 引言

什么是机器学习(Machine Learning)?

机器学习是这样一门学科，它致力于研究如何通过计算的手段，利用经验来改善系统自身的性能，在计算机系统中，“经验”通常以“数据”形式存在，因此，机器学习所研究的主要内容，是关于在计算机上从数据中产生“模型”(model)的算法，即“学习算法”(learning algorithm).有了学习算法，我们把经验数据提供给它，它就能基于这些数据产生模型；在面对新的情况时（例如看到一个没剖开的西瓜），模型会给我们提供相应的判断（例如好瓜），如果说计算机科学是研究关于“算法”的学问，那么类似的，可以说机器学习是研究关于“学习算法”的学问。

[Mitchell, 1997] 给出了一个更形式化的定义: 假设用 P 来评估计算机程序在某任务类 T 上的性能，若一个程序通过利用经验 E 在 T 中任务丰获得了性能改善, 则我们就说关于 T 和 P , 该程序对 E 进行了学习.

本书用 "模型"泛指从数据中学得的结果.

1.2 基本术语

假定我们收集了一批关于西瓜的数据, 例如(色泽=青绿; 根蒂=蜷缩; 敲声=浊响), (色泽=乌黑; 根蒂=稍蜷; 敲声=沉闷), (色泽=浅白; 根蒂=硬挺; 敲声=清脆), ……, 每对括号内是一条记录, "=“意思是"取值为”.

术语	含义	示例	数学描述
数据集 (data set)	一组记录的集合	一批关于西瓜的数据	D={x1,x2,⋯,xm}D = \left \{ \boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_m \right \}D={x1​,x2​,⋯,xm​}
示例 (instance) / 样本 (sample) / 特征向量 (feature vector)	关于一个事件或对象的描述	(色泽=青绿; 根蒂=蜷缩; 敲声=浊响) / 属性张成空间中的每个点对应的一个坐标向量	${\mathbf{x}}_i=(x_{i1};x_{i2};\cdots ,x_{id})$
属性 (attribute) / 特征 (feature)	反映事件或对象在某方面的表现或性质的事项	色泽, 根蒂, 敲声	$x_{ij}$是${\mathbf{x}}_i$的第$j$个属性对应的取值
属性值 (attribute value)	属性上的取值	“青绿”, “乌黑”	$x_{ij}$
属性空间 (attribute space) / 样本空间 (sample space) / 输入空间	属性张成的空间	把"色泽", “根蒂”, "敲声"作为三个坐标轴，则它们张成一个用于描述西瓜的三维空间，每个西瓜都可在这个空间中找到自己的坐标位置	$d$ 维样本空间 $\mathcal{X}$
学习(learning) / 训练 (training)	从数据中学得模型	-	-
训练数据(training data)	训练过程中使用的数据	-	-
训练样本(training sample) / 训练示例(training instance)	训练数据中的每个样本	-	-
训练集(training set)	训练样本组成的集合	-	-
假设(hypothesis)	学得模型对应了关于数据的某种潜在的规律	-	$h(\mathbf{x})$
真相 / 真实(ground-truth)	潜在规律自身	-	-
学习器(learner)	学习算法在给定数据和参数空间上的实例化	-	-
标记(label)	关于示例结果的信息	好瓜	$y_i\in \mathcal{Y}$
样例(example)	拥有了标记信息的示例	((色泽=青绿; 根蒂=蜷缩; 敲声=浊响)，好瓜)	$({\mathbf{x}}_i,y_i)$
标记空间(label space)/输出空间	所有标记的集合	-	$\mathcal{Y}$

• 欲预测的是离散值, 此类学习任务称为分类(classification);
• 欲预测的是连续值, 此类学习任务称为回归(regression).

对于二分类(binary classification)任务, 通常称其中一个类为"正类" (positive class), 另一个类为"反类"(negative class);
涉及多个类别时, 则称为多分类(multi-class classification)任务

学得模型后，使用其进行预测的过程称为测试(testing), 被预测的样本称为测试样本(testing sample).

聚类 (clustering) : 将训练集中的西瓜分成若干组，每组称为一个簇(cluster)

根据 训练数据是否拥有标记信息，学习任务可大致划分为两大类:

• 有监督学习(supervised learning) : 分类, 回归;
• 无监督学习(unsupervised learning) : 聚类;

泛化能力: 学得模型适用于新样本的能力. 具有强泛化能力的模型能很好地适用于整个样本空间.

1.3 假设空间

归纳与演绎
归纳(induction)与演绎(deduction)是科学推理的两大基本手段.
前者是从特殊到一般的泛化 (generalization)过程，即从具体的事实归结出一般性规律;
后者是从一般到特殊的特化 (specialization)过程，即从基础原理推演出具体状况.

例如，在数学公理系统中，基于一组公理和推理规则推导出与之相洽的定理，这是演绎; 而"从样例中学习"显然是一个归纳的过程, 因此亦称"归纳学习" (inductive learning).

归纳学习

• 广义: 从样例中学习;
• 狭义: 从训练数据中学得概念(concept), 因此亦称为"概念学习"或"概念形成".

概念学习/概念生成
最基本的是布尔概念学习, 即对"是" "不是"这样的可表示为 0/1 布尔值的目标概念的学习.

学习过程看作一个在所有假设(hypothesis)组成的空间中进行搜索的过程, 搜索目标是找到与训练集"匹配"(fit) 的假设, 即能够将训练集中的瓜判断正确的假设.假设的表示一旦确定, 假设空间及其规模大小就确定了.

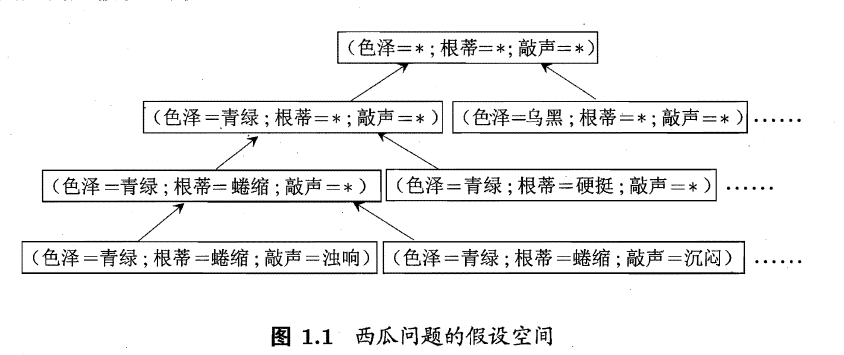
假设空间大小的计算

以如何判断一个西瓜是不是好瓜问题为例, 假设这个西瓜是不是好瓜可以有三种属性确定，分别为“色泽”，“根蒂”，“敲声”，同时每种属性有三种可能的情况，那么假设空间的规模是多少? 或者说在我们判断一个瓜是不是好瓜有多少种可能出现的情况?
假设每个属性有三种取值, 那么首先由简单的排列组合即可知道所有的属性情况为 $3\times 3\times 3$ 种.

但是在这种判断中, 默认了一个瓜是不是好瓜, 需要通过对西瓜的三种属性进行判断, 然而也许判断一个瓜是不是好瓜，压根不需要三种属性的确定, 可能一种属性, 比如只要色泽乌黑的西瓜全是好瓜, 那么此时其他两种属性都不再需要，也就是可以表述为 $\ast$，那么此时对每种属性的设置，除了我们给出的三种，我们还可以给出任意 $\ast$, 这样我们就得到了 $4\times 4\times 4$ 种.

上面都是判断一个瓜是不是好瓜, 那么我们默认这些假设中有总有好瓜的情况, 但是如果好瓜压根不存在, 那么好瓜的概念压根就不存在, 我们用 $\varnothing$ 表示这个假设. 则我们面临的假设空间规模大小为 $4\times 4\times 4+1=65$.

假定有 $k$ 种属性, 每种属性的取值各有 $n_1,n_2,\cdots ,n_k$种, 则该问题假设空间大小为:
$$(n_1+1)\times (n_2+1)\times \cdots \times (n_k+1)+1$$

参考 假设空间规模计算

搜索策略
自顶向下、从一般到特殊, 或是自底向上、从特殊到一般

版本空间
可能有多个假设与训练集一致，即存在着一个与训练集一致的"假设集合"，我们称之为"版本空间" (version space). 与西瓜数据集对应的版本空间如下

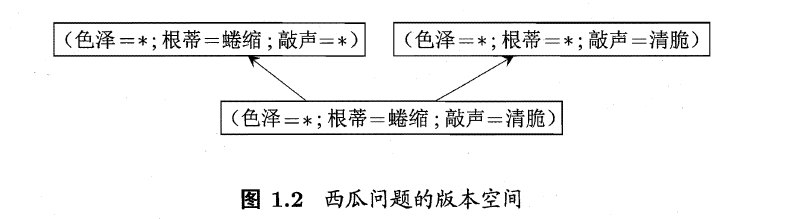
1.4 归纳偏好

机器学习算法在学习过程中对某种类型假设的偏好，称为"归纳偏好" (inductive bias), 或简称为"偏好". 任何一个有效的机器学习算法必有其归纳偏好, 否则它将被假设空间中看似在训练集上"等效"的假设所迷惑, 而无法产生确定的学习结果.

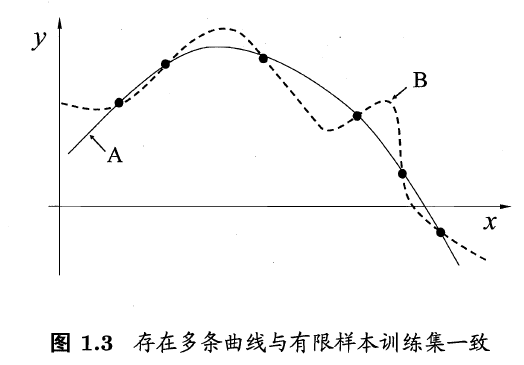
奥卡姆剃刀 (Occam’s razor)是一种常用的, 自然科学研究中最基本的原则来引导算法确立"正确的"偏好，即"若有多个假设与观察一致，则选最简单的那个".

"没有免费的午餐"定理(No Free Lunch Theorem，简称 NFL 定理)

假设样本空间 $\mathcal{X}$ 和假设空间 $\mathcal{H}$ 都是离散的. 令 $P(h\mid X,{\mathfrak{L}}_a)$ 代表算法 ${\mathfrak{L}}_a$ 基于训练数据 $X$ 产生假设 $h$ 的概率，再令 $f$ 代表我们希望学习的真实目标函数. ${\mathfrak{L}}_a$ 的 “训练集外误差”，即${\mathfrak{L}}_a$在训练集之外的所有样本上的误差为:
$$E_{ote}({\mathfrak{L}}_a\mid X,f)=\sum _h\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))P(h\mid X,{\mathfrak{L}}_a)$$
其中$\mathbb{I}(\cdot )$是指示函数，若 $\cdot$ 为真则取值1，否则取值0.
考虑二分类问题, 且真实目标函数可以是任何函数 X↦{0,1}\mathcal{X} \mapsto \left \{0, 1 \right \}X↦{0,1}，函数空间为 {0,1}∣X∣\left \{0, 1 \right \}^{|\mathcal{X}|}{0,1}∣X∣. 对所有可能的 $f$ 按均匀分布对误差求和, 有
$$\begin{array}{rl}\sum _f{E}_{ote}({\mathfrak{L}}_a\mid X,f)& =\sum _f\sum _h\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))P(h\mid X,{\mathfrak{L}}_a)\\ & =\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\sum _{h}P(h\mid X,{\mathfrak{L}}_a)\sum _f\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))\\ & =\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\sum _{h}P(h\mid X,{\mathfrak{L}}_a)\frac{1}{2}{2}^{|\mathcal{X}|}\\ & =\frac{1}{2}{2}^{|\mathcal{X}|}\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\sum _{h}P(h\mid X,{\mathfrak{L}}_a)\\ & =2^{|X|-1}\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\cdot 1\end{array}$$
其中, $E$ 表示期望, ${}_{ote}$ 表示训练集外误差, $P(\mathbf{x})$ 表示每种组合的概率.

此处证明可能较难理解, 这里参考博客 机器学习公式推导【Day1】NFL定理 给出详细解释

式$(1)$将误差式对 $f$ 进行求和, 对比误差表达式和式$(1)$即可理解.

式$(2)$对式$(1)$的重新排列, 将仅与 $\mathbf{x},f,h$ 各自有关的函数分离.

式$(3)$主要计算了
$$\sum _f\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))=\frac{1}{2}{2}^{|\mathcal{X}|}$$
这个结果首先需要明白$f$是任何能将样本映射到{0,1}\{0,1\}{0,1}的函数且为均匀分布, 也即不止有一个 $f$ 且每个 $f$ 出现的概率相等. 假设样本空间 X={x1,x2}\mathcal{X} = \{\boldsymbol{x}_1, \boldsymbol{x}_2\}X={x1​,x2​}, 即$|\mathcal{X}|=2$ , 那么所有$f$为
$$\begin{array}{rl}{f}_1& :f_1({\mathbf{x}}_1)=0,f_1({\mathbf{x}}_2)=0\\ f_2& :f_2({\mathbf{x}}_1)=0,f_2({\mathbf{x}}_2)=1\\ f_3& :f_3({\mathbf{x}}_1)=1,f_3({\mathbf{x}}_2)=0\\ f_4& :f_4({\mathbf{x}}_1)=1,f_4({\mathbf{x}}_2)=1\end{array}$$
共有$2^{|\mathcal{X}|}=2^2=4$个真实目标函数. 所以此时通过算法${\mathfrak{L}}_a$学习出来的模型$h(\mathbf{x})$对每个样本无论预测值为0还是1必然有一半的$f$与之预测值相等，例如，现在学出来的模型${\mathbf{x}}_1$的预测值为1，也即$h({\mathbf{x}}_1)$, 那么有且只有 $f_3$ 和 $f_4$​与$h({\mathbf{x}}_1)$的值相等, 也就是有且只有一半的 $f$ 与它预测值相等, 所以${\sum }_f\mathbb{I}(h(\mathbf{x})\ne f(\mathbf{x}))=\frac{1}{2}{2}^{|\mathcal{X}|}$

式$(4)$仅进行了移项操作.

式$(5)$是由于所有可能事件的概率之和为1, 故有 ${\sum }_{h}P(h\mid X,{\mathfrak{L}}_a)=1$ .

该定理表明总误差与学习算法无关.

值得一提的是, 在这里我们定义真实的目标函数为任何能将样本映射到 {0,1}\{0,1\}{0,1} 的函数且为均匀分布，但是实际情形并非如此，通常我们只认为能高度拟合已有样本数据的函数才是真实目标函数，例如，现在已有的样本数据为 {(x1,0),(x2,0)}\left\{\left(\boldsymbol{x}_{1}, 0\right),\left(\boldsymbol{x}_{2}, 0\right)\right\}{(x1​,0),(x2​,0)}, 由于没有收集到或者压根不存在 {(x1,1),(x2,0)},{(x1,1),(x2,1)}\left\{\left(\boldsymbol{x}_{1}, 1\right),\left(\boldsymbol{x}_{2}, 0\right)\right\},\left\{\left(\boldsymbol{x}_{1}, 1\right),\left(\boldsymbol{x}_{2}, 1\right)\right\}{(x1​,1),(x2​,0)},{(x1​,1),(x2​,1)}这类样本，所以$f_1,f_3,f_4$都不算是真实目标函数.

所以, NFL 定理最重要的寓意是让我们清楚地认识到，脱离具体问题，空泛地谈论"什么学习算法更好" 毫无意义, 因为若考虑所有潜在的问题, 则所有学习算法都一样好.要谈论算法的相对优劣, 必须要针对具体的学习问题; 在某些问题上表现好的学习算法, 在另一些问题上却可能不尽如人意, 学习算法自身的归纳偏好与问题是否相配, 往往会起到决定性的作用.