基础算法---【前缀和】
前言
前缀和的核⼼思想是预处理,可以在暴⼒枚举的过程中,快速给出查询的结果,从⽽优化时间复杂度。是经典的⽤空间替换时间的做法。
题目一:【模板】前缀和
https://www.nowcoder.com/share/jump/5581804081758411915028
解题思路
前缀和可以快速求数组某个区间的和,本题的第一步就是先预处理出一个前缀和数组,第二步就是利用前缀和数组去获得答案。
前缀和数组取名为f,题目给的数组记为a(数组从下标为1开始存),f[i] 表示的就是a数组下标 [1 , i] 所有元素的和,而f[i] 可以由 f[i - 1] + a[i] 来算出。
假设a数组为 [1 , 2 , 3 , 4 , 5]
f数组为 [1 , 3 ................
下标 1 2 3 4 5
由上边的例子可以更好理解上边提到的 f[i] 的计算方式。
最后一个问题就是如何利用f数组来计算题目给出的 l~r 的区间和呢?如果 l 为2,r 为4,那么 l~r 的区间和就可以由 f[4] - f[1] 来计算,类推一下就得出了计算方式,即为 f[r] - f[l - 1]
代码实现
#include<iostream>
using namespace std;const int N = 1e5 + 10;
int a[N];//a数组存放题给数据
long long f[N];//a数组里边的元素和可能会超出int的范围int n, m;int main()
{cin >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i];}//处理前缀和数组for (int j = 1; j <= n; j++){f[j] = f[j - 1] + a[j];}while (m--){int l, r;cin >> l >> r;cout << f[r] - f[l - 1] << endl;}return 0;
}题目二:最大子段和
https://www.luogu.com.cn/problem/P1115
解题思路
要想求所有子段和的最大值,只需要求出以 a[i] 为最后一个元素的所有子段中的最大值就可以了。最后循环一整个a数组取最终的最大值就是我们想要的结果。而要想求 a[i] 所有子段的最大值,我们仅需要求出 f 数组里边下标为 [1,i-1]中的最小值(记作prevmin),最后用 f[i] - prevmin 就可以了。

代码实现
#include<iostream>
using namespace std;const int N = 2e5 + 10;
long long f[N];//不用再创建a数组了,因为本题只需要计算前缀和就能解决问题
long long n;int main()
{cin >> n;for (int i = 1; i <= n; i++){int x;cin >> x;f[i] = f[i - 1] + x;}//负无穷大//ret表示最终的最大子段和long long ret = -1e20;//a[i]之前的所有前缀和里边最小的。long long prevmin = 0;for (int i = 1; i <= n; i++){ret = max(ret, f[i] - prevmin);prevmin = min(prevmin, f[i]);//计算下一次[1,i-1]区间里边的最小值}cout << ret << endl;return 0;
}
题目三:【模板】二维前缀和
https://www.nowcoder.com/share/jump/5581804081758530268753
解题思路
二维前缀和是用于求解矩阵某个区间的和的,本题的解题思路就是先用一个二维矩阵去预处理矩阵的和,假设这个前缀和数组为f,那么 f[i][j] 就表示从 [1 , 1] ~ [i , j] 的所有元素的和。请看下图。

预处理好了f数组之后就可以开始解决我们题目要求的问题了,再看下边的一张图。
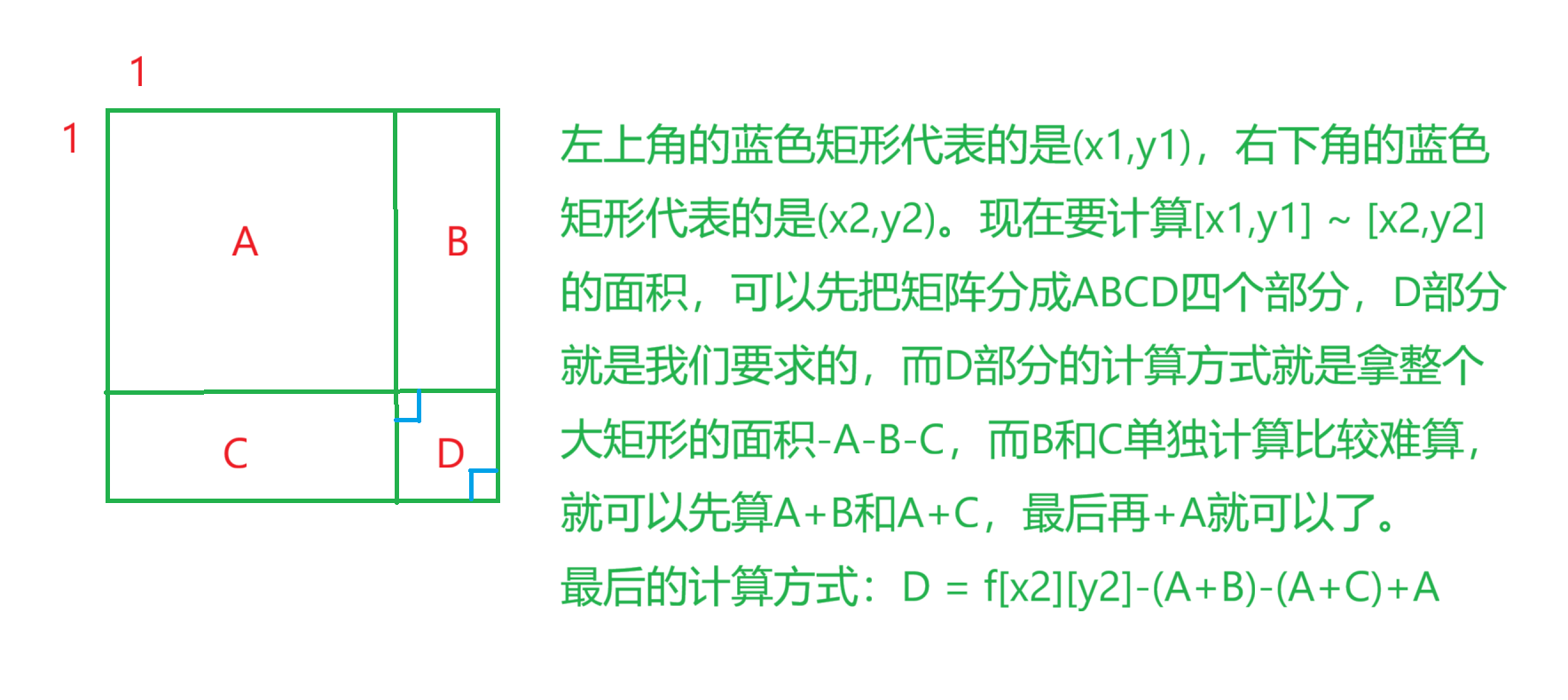
代码实现
//注意:下边的a矩阵也可以不要,直接就计算f也可以
#include<iostream>
using namespace std;const int N = 1e3 + 10;
typedef long long LL;int n, m, q;
int a[N][N];
LL f[N][N];//前缀和数组int main()
{cin >> n >> m >> q;for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){cin >> a[i][j];}}//计算f数组for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){f[i][j] = f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1] + a[i][j];}}while(q--){//int x1, y1;int x2, y2;cin >> x1 >> y1 >> x2 >> y2;cout << f[x2][y2] - f[x1 - 1][y2] - f[x2][y1 - 1] + f[x1 - 1][y1 - 1] << endl;}return 0;}