当前位置：首页 > news >正文

atcoder经典好题

news 2025/9/23 8:48:34

D - Forbidden Difference

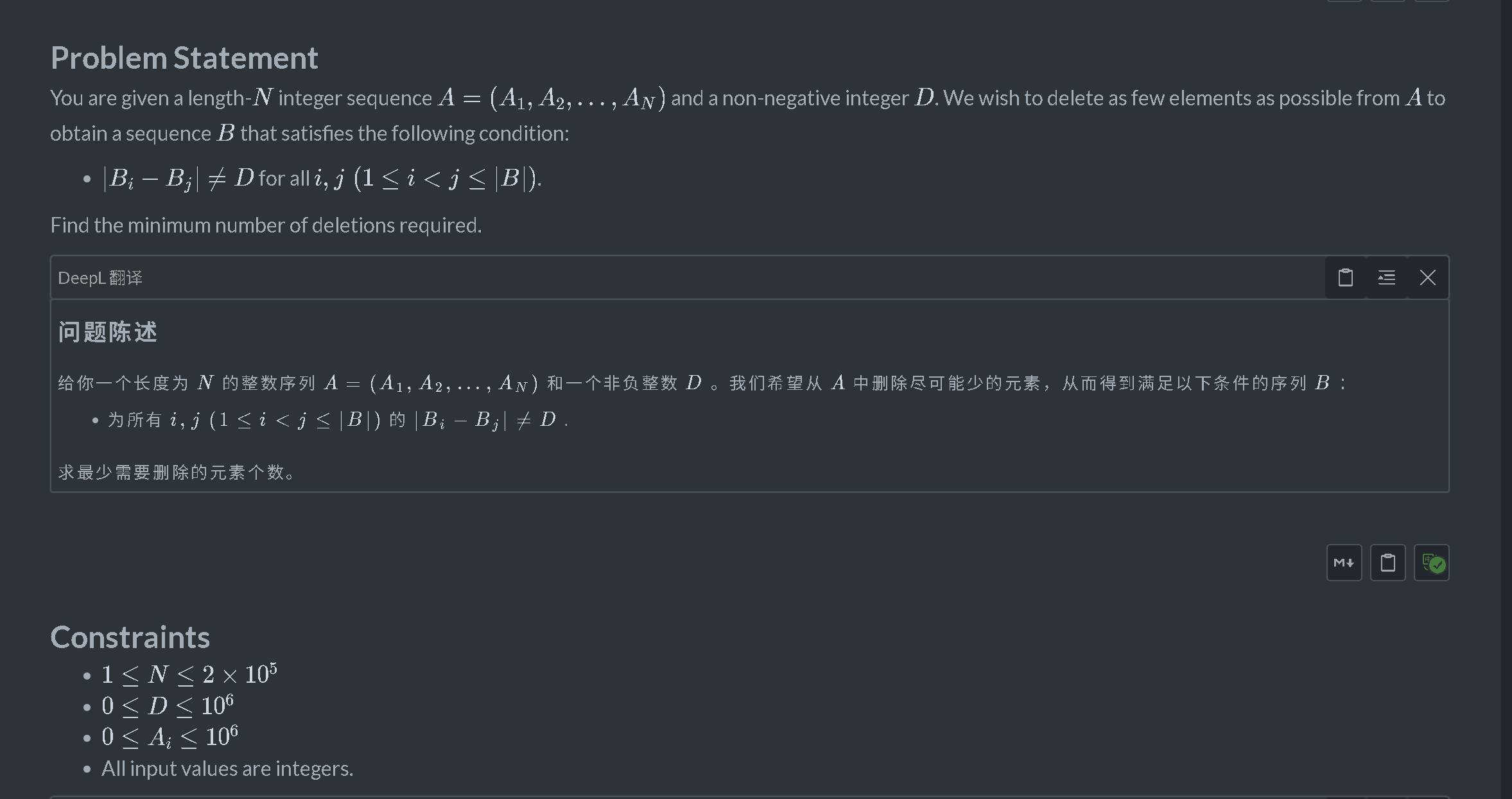
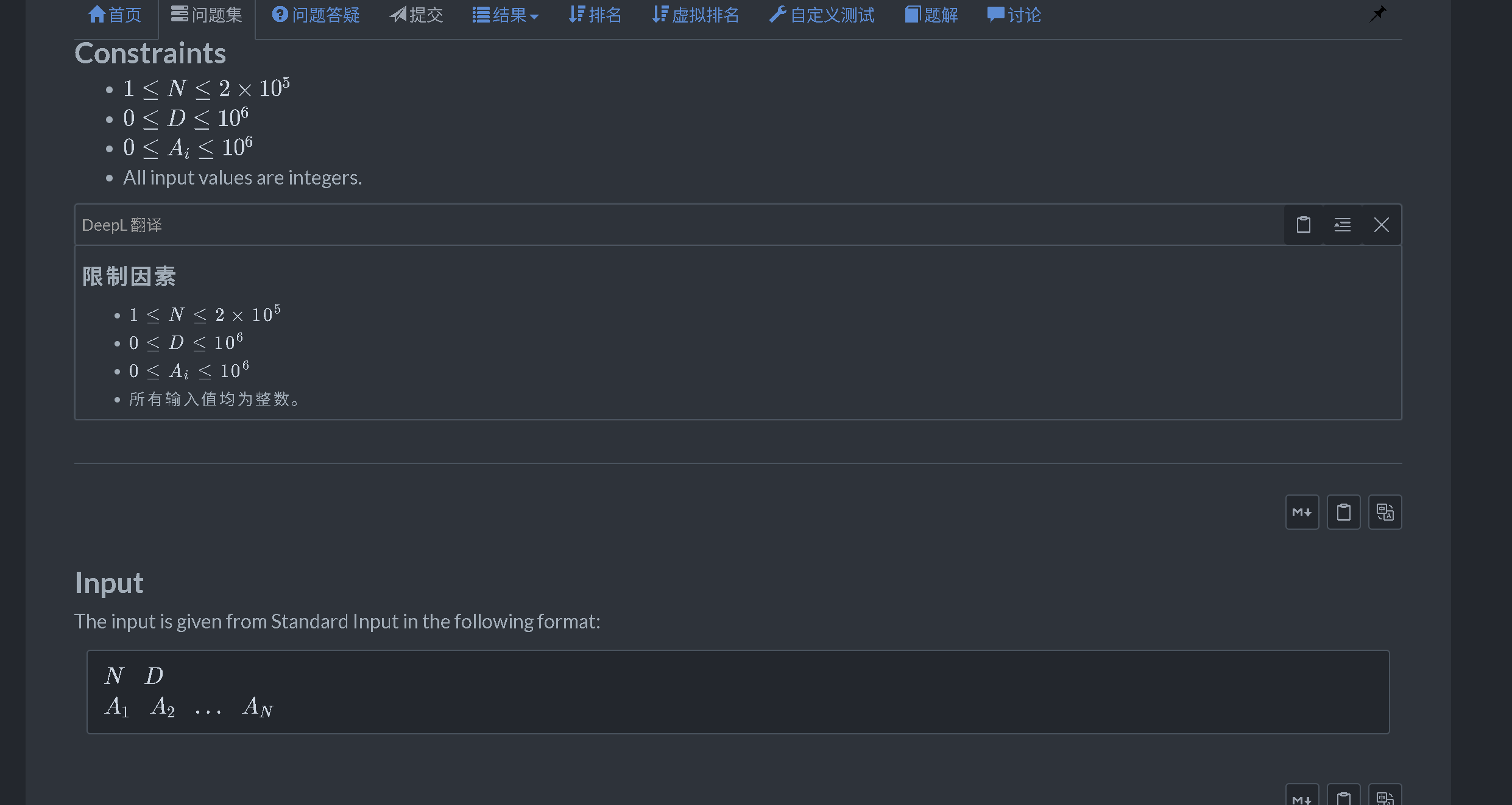
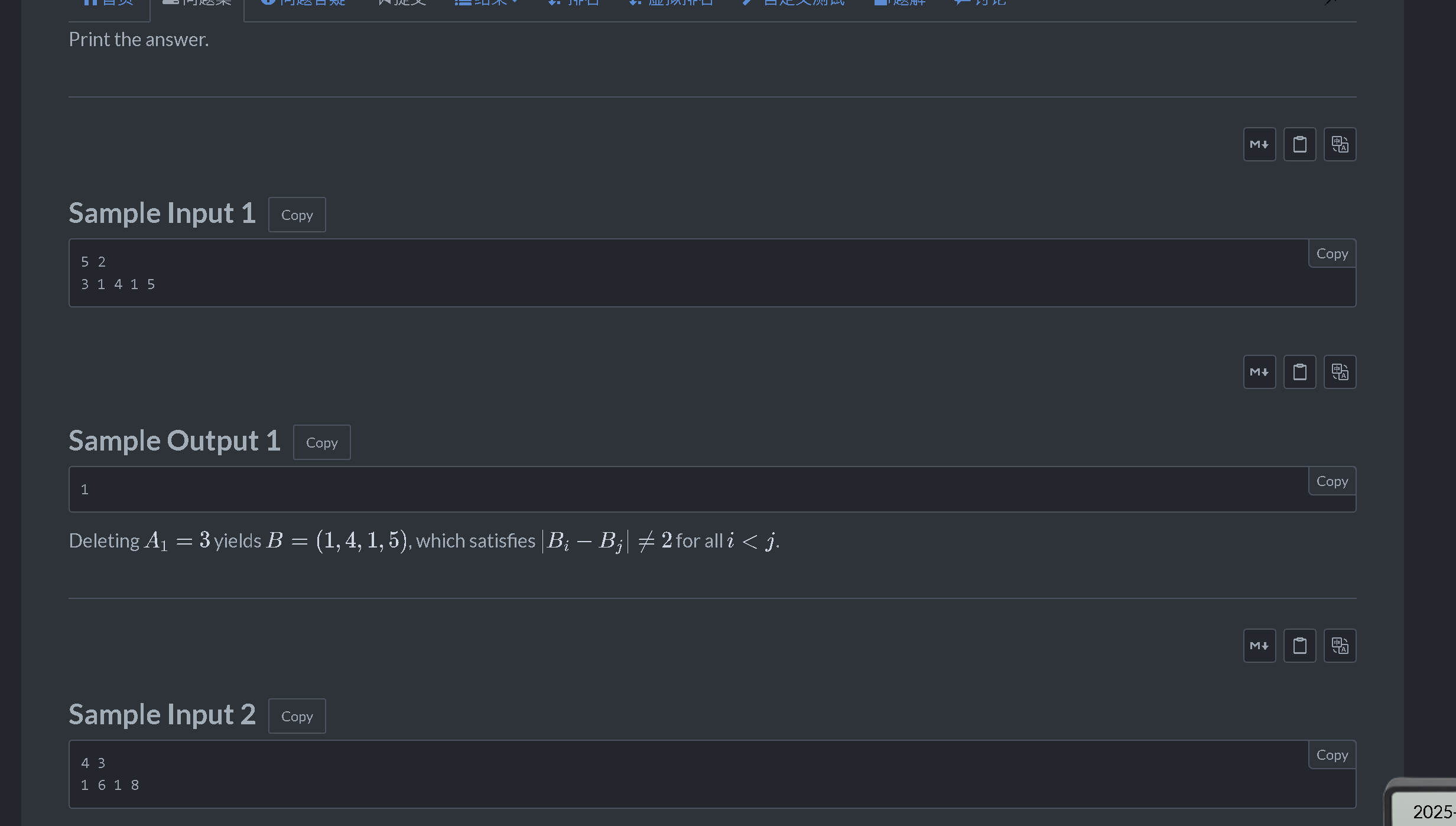
题意：给你一段序列，问你最少删多少个元素，删后使得任意元素两两之间差的绝对值不等于题目中给定的值。

思路：如果两个元素两两差的绝对值等于m，则必有|a - b| % m == a % m - b % m; 所以我们将数按照模m的值进行划分，对于一组模值一致的数，我们就要判断数字之间是否相等，进行排序以更好的判断，考虑用dp表示所有状态的取值，dp[n][2]，dp[i][0]，表示到第i个数时，不删除这个数的最小答案，dp[i][1]，表示到第i个数时，删除这个数时的最小答案，根据这种状态划分，有三种情况：当a[i] == a[i-1]时，dp[i][0] = dp[i-1][0], dp[i][1] = dp[i-1][1] + 1, 当a[i] == a[i-1] + m时，dp[i][0] = dp[i-1][1], dp[i][1] = min(dp[i-1][0], dp[i-1][1]) + 1, 当a[i] != a[i-1] + m && a[i] != a[i-1]时，dp[i][0] =

min(dp[i-1][0], dp[i-1][1]), dp[i][1] = min(dp[i-1][0], dp[i-1][1]) + 1;

特殊的，要判断m是否等于0，当m等于0时，只需开一个set距离有多少个不同数，然后用n减去有多少个不同的数即为答案。

代码：

void solve()
{int n, m;cin >> n >> m;if (m == 0){set<int> s;for (int i = 0; i < n; i ++ ){int x; cin >> x;s.insert(x);}cout << n - s.size() << endl;return ;}vector<vector<int>> a(m);for (int i = 0; i < n; i ++ ){int x; cin >> x;a[x % m].push_back(x);}for (int i = 0; i < m; i ++ ){sort(a[i].begin(), a[i].end());}int ans = 0;for (int i = 0; i < m; i ++ ){if (a[i].empty()) continue;vector<array<int,2>> dp(a[i].size());//0表示没删，1表示删dp[0][1] = 1;for (int j = 1; j < a[i].size(); j ++ ){if (a[i][j] == a[i][j-1]){dp[j][0] = dp[j-1][0];dp[j][1] = dp[j-1][1] + 1;}else if (a[i][j] == a[i][j-1] + m){dp[j][0] = dp[j-1][1];dp[j][1] = min(dp[j-1][0], dp[j-1][1]) + 1;}else{dp[j][0] = min(dp[j-1][0], dp[j-1][1]);dp[j][1] = min(dp[j-1][0], dp[j-1][1]) + 1;}}ans += min(dp[a[i].size()-1][0], dp[a[i].size()-1][1]);}cout << ans << endl;
}

链接：D - Forbidden Difference

E - Subarray Sum Divisibility

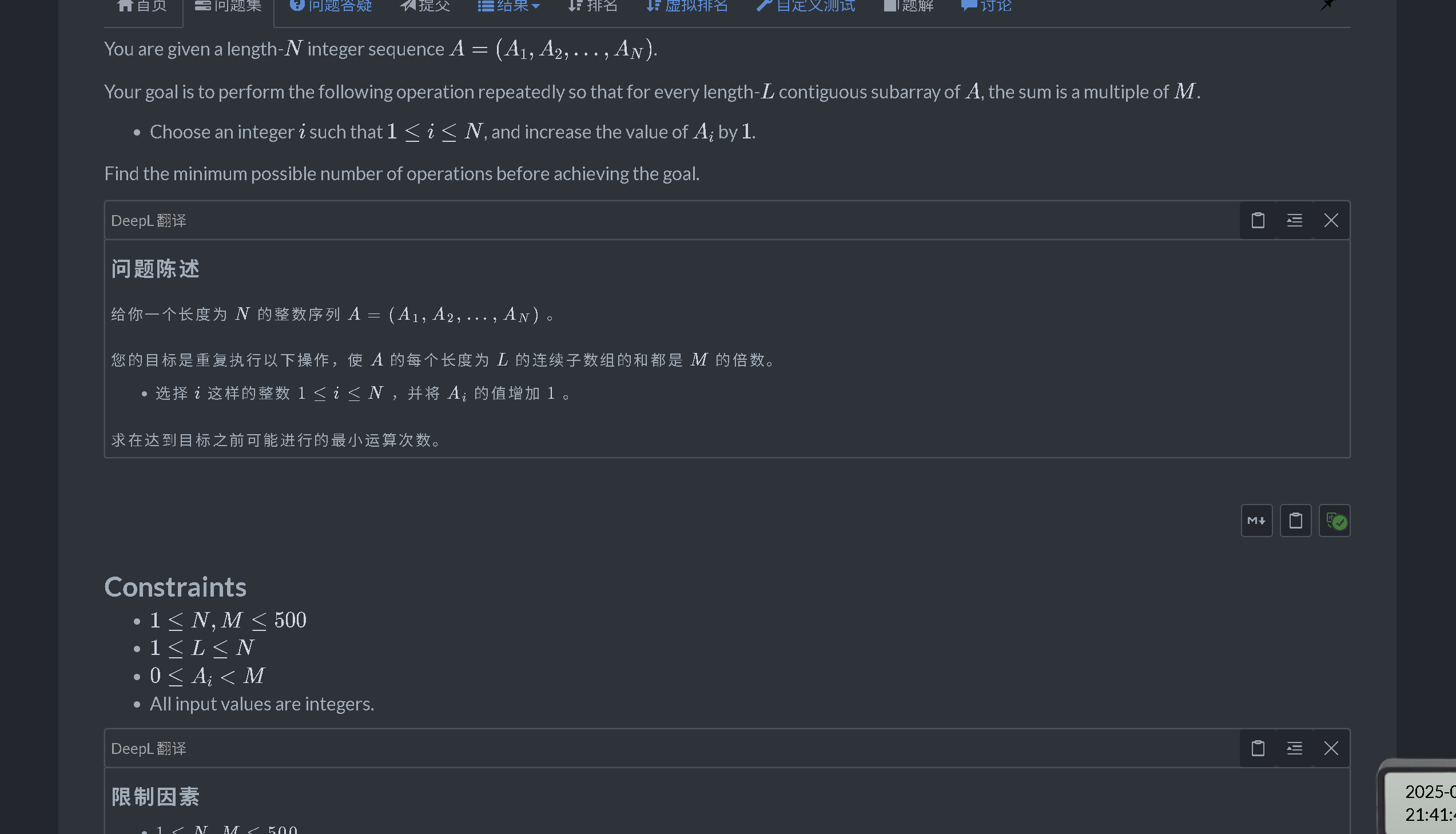
题目大意：让你通过给某一个元素加1的操作，最后使连续L的子数组元素之和是M的倍数，求使达目的的最小操作次数

思路：考虑一段长为L且已经是和为m的倍数的区间，当到第j + 1位置时，由数学性质，a[j+1] % m == a[j-L+1] % m; 所以当第一段长为L的数已经确定了的时候，由于 a[j] % m == a[j+L] % m ==a[j+2*L] % m == .... ==a[j + n*L] % m; 所以只需要枚举前m个元素的取值即可,根据数据范围，和题目性质，我们可以使用dp做法，因为前m个数选定时，后续数字对答案的贡献也是固定的，所以我们先预处理出，每种情况对答案的贡献，令g[i][j]表示当第i个数%m的余数是j时后续所有i+L,i+2*L...i+n*L的元素对答案的影响，令f[i][j]表示当选到第i个数时，总和模m为j的最小操作次数；转移方程为f[i][j] = min(f[i][j],f[i-1][(j-p+k)%k] + g[i][p]), p为第i个数模m的余数为p，最后输出f[m][0]即可

代码：

int32_t main()

{

ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);

int n,m,k;

cin >> n >> k >> m;

vector<int> v(n+1);

for (int i = 1; i <= n; i ++ ) cin >> v[i];

vector<vector<int>> g(m+1,vector<int>(k)), f(m+1,vector<int>(k,0x3f3f3f3f));

f[0][0] = 0;

for (int i = 1; i <= m; i ++ )

for (int j = 0; j < k; j ++ )

for (int p = i; p <= n; p += m)

{

g[i][j] += (j - v[p] + k) % k;

}

for (int i = 1; i <= m; i ++ )

for (int j = 0; j < k; j ++ )

for (int p = 0; p < k; p ++ )

f[i][j] = min(f[i][j],f[i-1][(j - p + k) % k] + g[i][p]);

cout<<f[m][0]<<endl;

return 0;

}

链接：E - Subarray Sum Divisibility

D - 2x2 Erasing 2

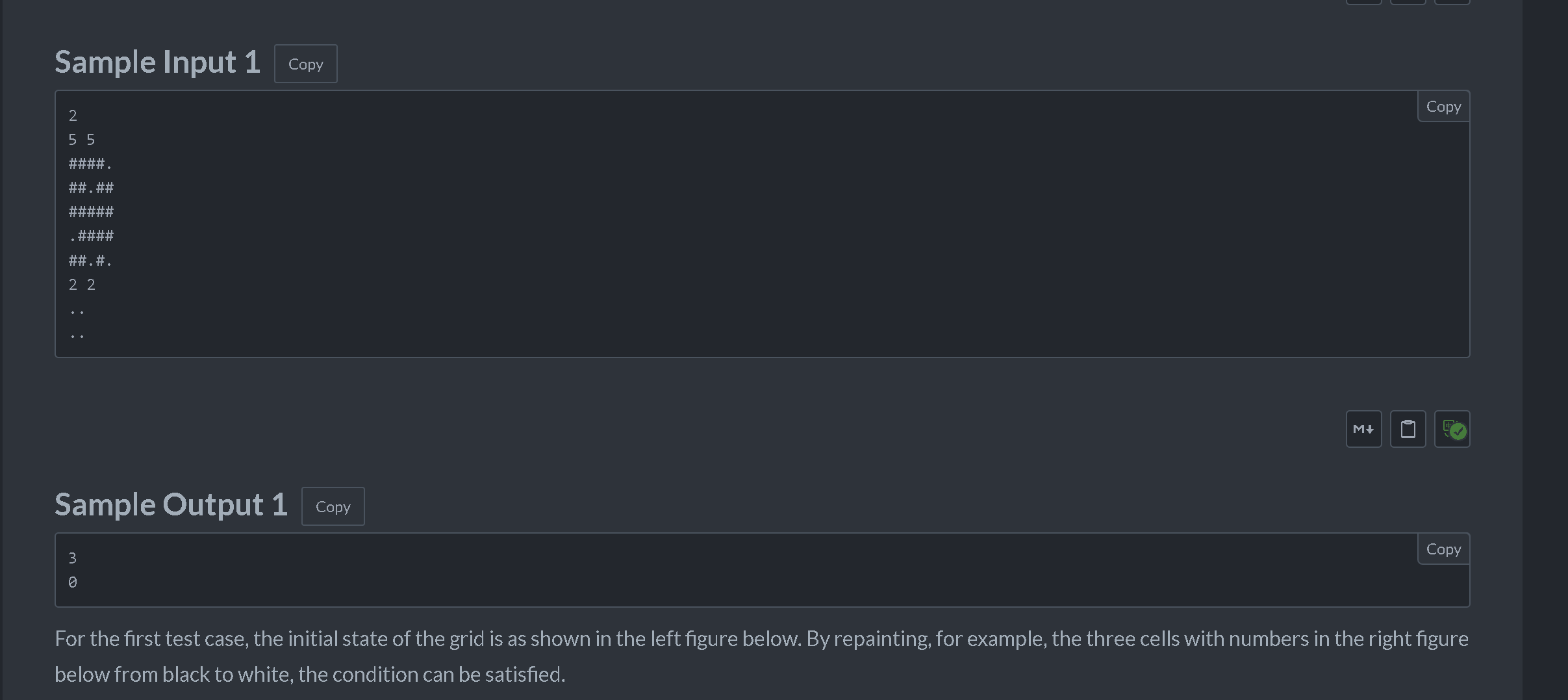
思路：数据范围小，可以进行爆搜，也可以进行状压dp

定义dp[i][s]表示，到第i行时，第i行状态表示为s时的最小操作次数

a[i]表示一开始输入的状态,通过枚举i-1和i的状态进行状态转移，先令s = s1 & s2 等于s1，s2中有共同黑块的位置，需要判断s中是否有相邻的黑色块，可以通过让s向左或向右移位然后&s是否为1的操作，判断是否有黑色块，如果有黑色块则不能从s1状态转移到s2状态，如果可以从s1转移到s2，则转移方程为,dp[i][s2] = min(dp[i][s2], dp[i-1][s1] + __builtin_popcount(a[i] ^ s2) // s2与ai数位不相同的位数;

代码

#include<bits/stdc++.h>

#define endl "\n"
//#define int long long

using namespace std;
const int N = 10, S = (1 << 7) + 5, INF = 1e9;
int n, m;
int dp[N][S+5];
int a[N];

void solve()
{
cin >> n >> m;
for(int i = 1; i <= n; i ++ )
{
string s; cin >> s;
a[i] = 0;
for(int j = 1; j <= m; j ++ )
if(s[j - 1] == '#')
a[i] |= (1 << (j - 1));
}
for(int i = 0; i <= n; i ++ )
for(int s = 0; s < (1 << m); s ++ )
dp[i][s] = INF;
dp[0][0] = 0;
for(int i = 1; i <= n; i ++ )
{
for(int s1 = 0; s1 < (1 << m); s1 ++ )
for(int s2 = 0; s2 < (1 << m); s2 ++ )
{
int s = s1 & s2;
if(s & (s >> 1)) continue;
dp[i][s2] = min(dp[i][s2], dp[i-1][s1] + __builtin_popcount(s2 ^ a[i]));
}
}
int ans = INF;
for(int i = 0; i < (1 << m); i ++ )
ans = min(ans, dp[n][i]);
cout << ans << endl;
}