当前位置：首页 > news >正文

【不背八股】15.kmp算法/ Dijkstra算法/二叉树遍历

news 2025/9/22 11:49:34

引言

在最近的笔试中，看到某些题型：KMP算法、Dijkstra算法等，以前学过，但印象不深，本文重新来温故梳理一下。

1. KMP算法

KMP 算法的核心在于：当匹配失败时，模式串并不需要完全回退，而是通过 部分匹配表（next 数组） 来决定下一步从哪里继续匹配。

换句话说，它利用了“已经匹配的前缀和后缀”之间的关系，避免了对主串的重复扫描。

如下图[1]所示：

当字串C和主串A出现不匹配时，找到next数组前一个值(2)，即跳过2个字符再开始匹配。

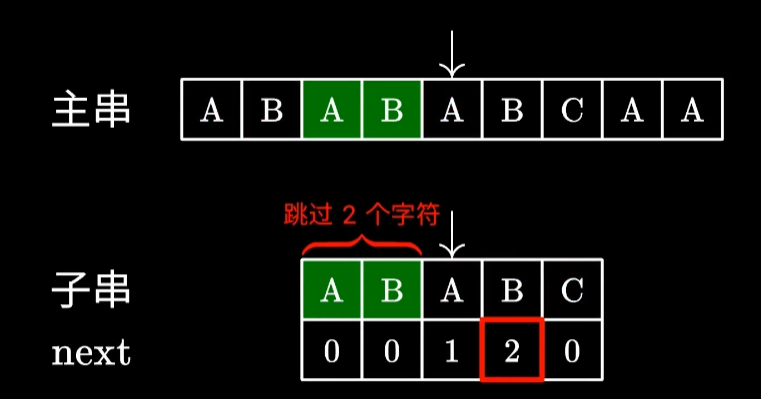
用程序可以表示如下：

vector<int> KMP(const string& text, const string& pattern) {vector<int> result;vector<int> next = buildNext(pattern);int n = text.size();int m = pattern.size();int j = 0;  // 当前匹配的模式串长度for (int i = 0; i < n; i++) {while (j > 0 && text[i] != pattern[j]) {j = next[j - 1];  // 利用 next 回退}if (text[i] == pattern[j]) {j++;}if (j == m) {result.push_back(i - m + 1); // 记录匹配起始位置j = next[j - 1];            // 继续寻找下一个匹配}}return result;
}

进一步思考，next数组是如何构建的？

next数组本质是记录相同前缀的长度，例如，下图第二个A发现前面已经有一个A了，next数组的对应位置就为1，第二个B发现前面已经有一个AB的共同前缀，next数组的对应位置就为2。

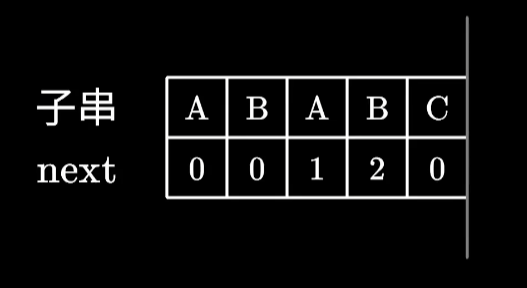
构建next数组的过程中，如果遇到下一个字符和前面不匹配的情况，并不是从头开始重新匹配，而是回退到上一个位置开始匹配，也是节省时间的一个小技巧，具体的代码如下：

vector<int> buildNext(const string& pattern) {int m = pattern.size();vector<int> next(m, 0);int j = 0;  // 已匹配的前缀长度for (int i = 1; i < m; i++) {while (j > 0 && pattern[i] != pattern[j]) {j = next[j - 1];  // 回退}if (pattern[i] == pattern[j]) {j++;}next[i] = j;}return next;
}

2. Dijkstra算法

Dijkstra 算法属于单源最短路径问题，其理论基础是最短路径的最优子结构性质:

性质：如果从源点 $s$ 到终点 $t$ 的最短路径是 $\to … \to u \to v \to … \to t)$ ，
那么其中的子路径 $\to … \to u)$ 也是从 $s$ 到 $u$ 的最短路径。
意义：这说明可以通过逐步扩展最短路径来得到整体最优解，类似于贪心算法。

算法的具体思路如下图[2]所示

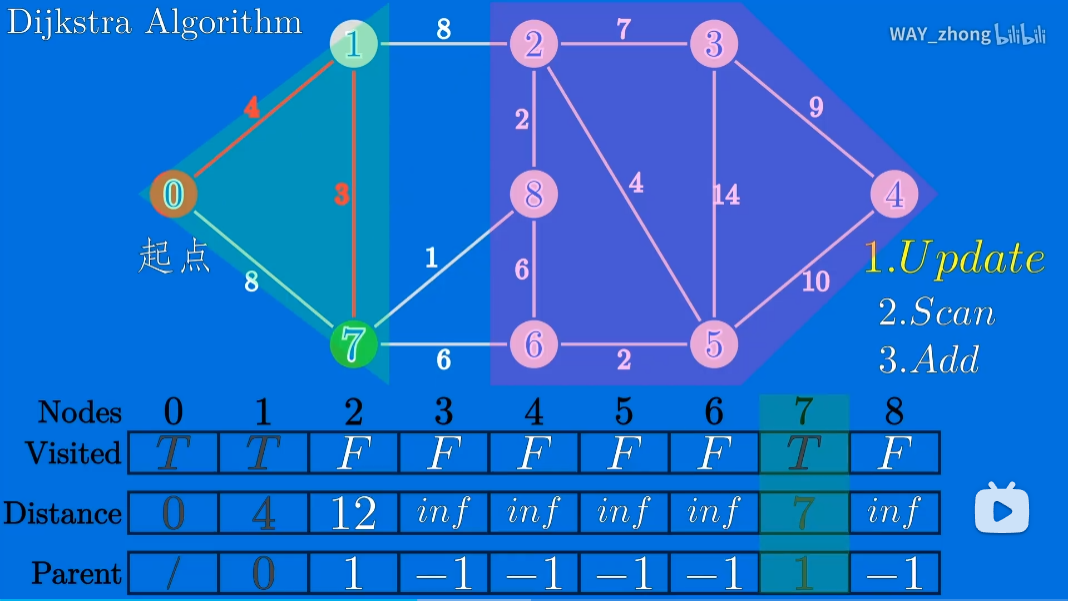
通过下面三个数组记录状态：

Visited：记录每个节点是否访问过
Distance：记录到起点到每一个节点的最短距离
Parent：记录该点的上一个节点值

Dijkstra 算法将图分成两部分：

1.已访问集合（Visited = true）

起点开始，逐步扩展。
集合中的点的最短路径已被确定，不会再改变。

2.未访问集合（Visited = false）

存放那些还没有被完全确认最短路径的节点。
它们的 Distance 值会随着算法进行不断被更新。

算法的循环过程是：

1.从未访问集合中，选择一个 当前距离最小 的节点 u。
2.将 u 标记为已访问（Visited[u] = true）。
3.遍历 u 的所有邻居 v，如果通过 u 到 v 的路径更短，则更新：

$D i s t an ce [v] = D i s t an ce [u] + w (u, v)$

并记录

$P a re n t [v] = u$
4.重复以上步骤，直到所有节点访问完毕，或者目标节点的最短路径已经确定。

3. 二叉树前序、中序、后序遍历

还有一类经典的题型是给定两个二叉树序列遍历，求另一个序列遍历。

基础知识

在二叉树的遍历中，最常见的三种遍历方式是：

前序遍历（Preorder Traversal）
- 访问顺序：根 → 左子树 → 右子树
- 例如：A B D E C F
中序遍历（Inorder Traversal）
- 访问顺序：左子树 → 根 → 右子树
- 例如：D B E A F C
后序遍历（Postorder Traversal）
- 访问顺序：左子树 → 右子树 → 根
- 例如：D E B F C A

已知前序和中序，求后序

思路解析

利用前序序列确定根节点
- 前序遍历的第一个元素一定是整棵树的根。
利用中序序列划分左右子树
- 在中序遍历中，根节点左边的部分是左子树，右边的部分是右子树。
递归处理子树
- 在左右子树中，重复上面的过程：
  - 利用前序找到根；
  - 在中序中分割；
  - 递归构建。
得到后序遍历
- 根据定义，先递归输出左子树，再递归输出右子树，最后输出根。

示例

假设：

前序：A B D E C F
中序：D B E A F C

过程如下：

前序首位 A → 根节点。
中序中 A 左边为 D B E（左子树），右边为 F C（右子树）。
左子树：
- 前序为 B D E
- 中序为 D B E
- 根为 B，左子树 D，右子树 E → 后序为 D E B。
右子树：
- 前序为 C F
- 中序为 F C
- 根为 C，左子树 F → 后序为 F C。
整体后序为：D E B F C A。

已知中序和后序，求前序

思路解析

利用后序序列确定根节点
- 后序遍历的最后一个元素一定是整棵树的根。
利用中序序列划分左右子树
- 在中序遍历中，根节点左边是左子树，右边是右子树。
递归处理子树
- 在左右子树中重复以上过程，逐步确定前序遍历。
得到前序遍历
- 根据定义，先输出根，再输出左子树，最后输出右子树。

示例

假设：

中序：D B E A F C
后序：D E B F C A

过程如下：

后序最后一个 A → 根节点。
中序中 A 左边为 D B E（左子树），右边为 F C（右子树）。
左子树：
- 中序为 D B E
- 后序为 D E B
- 根为 B，左子树 D，右子树 E → 前序为 B D E。
右子树：
- 中序为 F C
- 后序为 F C
- 根为 C，左子树 F → 前序为 C F。
整体前序为：A B D E C F。

已知前序和后序，求中序

这一类题型相对特殊：

仅凭前序和后序序列，无法唯一确定一棵二叉树（因为中间的划分不唯一）。
但如果题目限定为 满二叉树，则可以唯一确定。

思路解析（满二叉树条件下）

前序序列确定根节点
- 前序的第一个元素为根。
后序序列确定子树范围
- 在后序中，最后一个元素是根。
- 前序第二个元素一定是左子树的根，可以在后序中找到它的位置，从而确定左子树的范围。
递归划分左右子树
- 重复该过程，逐步恢复中序。
得到中序遍历
- 根据定义，先输出左子树，再输出根，最后输出右子树。

示例

假设：

前序：A B D E C F
后序：D E B F C A

过程如下（假设是满二叉树）：

前序首位 A → 根节点。
前序第二位 B 是左子树的根，在后序中找到 B，左子树范围是 D E B。
左子树：
- 前序为 B D E
- 后序为 D E B
- 中序为 D B E。
右子树：
- 前序为 C F
- 后序为 F C
- 中序为 F C。
整体中序为：D B E A F C。

总结

已知序列	可以唯一确定？	确定方法	求解目标	思路简述
前序 + 中序	✅ 可以唯一确定	前序首位 → 根；在中序中定位根 → 左右子树	后序	递归构建左右子树，后序为「左 → 右 → 根」
中序 + 后序	✅ 可以唯一确定	后序末位 → 根；在中序中定位根 → 左右子树	前序	递归构建左右子树，前序为「根 → 左 → 右」
前序 + 后序	❌ 一般情况不唯一 ✅ 满二叉树时唯一	前序首位 → 根；前序第二位定位左子树，在后序中找到范围	中序	满二叉树条件下，递归划分左右子树，中序为「左 → 根 → 右」