一维数组原地更新——力扣119.杨辉三角形II
【LeetCode题解 | Java】返回杨辉三角的第 rowIndex 行(进阶 O(k) 空间)
力扣119.杨辉三角形II
题目描述
在杨辉三角中,每个数是它左上方和右上方的数的和。
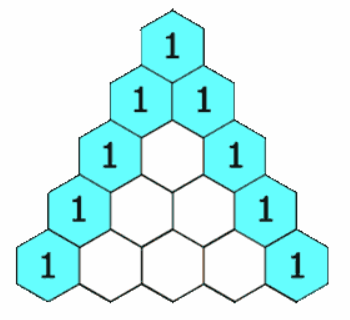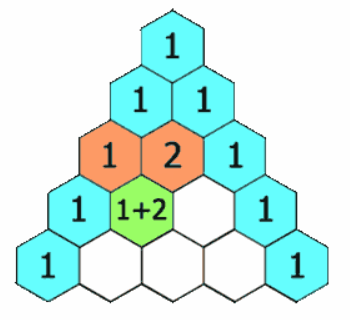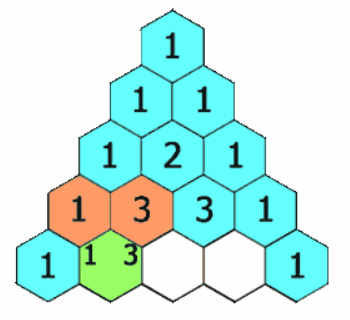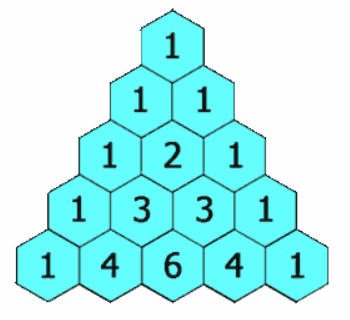
给定一个非负索引 rowIndex,返回杨辉三角的第 rowIndex 行。
示例:
输入: rowIndex = 3
输出: [1,3,3,1]输入: rowIndex = 0
输出: [1]输入: rowIndex = 1
输出: [1,1]
提示:
- 0 <= rowIndex <= 33
进阶:你能将算法优化到 O(rowIndex) 空间复杂度吗?
方法一:常规动态规划(O(k²) 时间,O(k²) 空间)
最直接的思路是把杨辉三角从第 0 行推到第 rowIndex 行,最后返回目标行。
思路:
- 每一行第一个和最后一个元素是 1。
- 其他位置由上一行的两个元素相加得到。
代码实现:
class Solution {public List<Integer> getRow(int rowIndex) {List<List<Integer>> triangle = new ArrayList<>();for (int i = 0; i <= rowIndex; i++) {List<Integer> row = new ArrayList<>();for (int j = 0; j <= i; j++) {if (j == 0 || j == i) {row.add(1);} else {row.add(triangle.get(i - 1).get(j - 1) + triangle.get(i - 1).get(j));}}triangle.add(row);}return triangle.get(rowIndex);}
}
复杂度分析:
- 时间复杂度:O(rowIndex²)
- 空间复杂度:O(rowIndex²)
这种方法容易理解,但空间复杂度没有优化。
方法二:一维数组原地更新(O(k²) 时间,O(k) 空间)
进阶要求让我们思考如何只用一行数组解决。核心技巧是从后往前更新。
思路:
- 准备一个长度为
rowIndex+1的数组,初始row[0] = 1。 - 对于每一行,从右往左更新:
row[j] = row[j] + row[j-1]。 - 避免了覆盖掉还没计算的数。
代码实现:
class Solution {public List<Integer> getRow(int rowIndex) {Integer[] row = new Integer[rowIndex + 1];Arrays.fill(row, 0);row[0] = 1;for (int i = 1; i <= rowIndex; i++) {for (int j = i; j > 0; j--) {row[j] = row[j] + row[j - 1];}}return Arrays.asList(row);}}
复杂度分析:
- 时间复杂度:O(rowIndex²)
- 空间复杂度:O(rowIndex)
这是最常见的面试解法,清晰且满足进阶要求。
方法三:组合数公式(O(k) 时间,O(1) 空间)
数学公式可以直接求解。杨辉三角的第 r 行就是:
C(r,0), C(r,1), ..., C(r,r)
其中 C(r,k) 表示组合数。
利用递推关系:
C(r,0) = 1
C(r,k+1) = C(r,k) * (r-k) / (k+1)
我们可以只用一次循环得到整行。
代码实现:
class Solution {public List<Integer> getRow(int rowIndex) {List<Integer> row = new ArrayList<>(rowIndex + 1);long val = 1;for (int k = 0; k <= rowIndex; k++) {row.add((int) val);val = val * (rowIndex - k) / (k + 1);}return row;}
}
复杂度分析:
- 时间复杂度:O(rowIndex)
- 空间复杂度:O(1)
这是最优解,数学味道更浓,代码简洁。
总结对比
| 方法 | 思路 | 时间复杂度 | 空间复杂度 | 特点 |
|---|---|---|---|---|
| 方法一 | 完整 DP 构造 | O(k²) | O(k²) | 简单直观 |
| 方法二 | 一维数组更新 | O(k²) | O(k) | 面试推荐,符合进阶要求 |
| 方法三 | 组合数公式 | O(k) | O(1) | 数学最优,代码简洁 |
最终推荐提交版本
我个人推荐 方法二,既容易解释,也满足进阶要求。如果面试官追问,还可以补充方法三展示深度。
最终提交代码如下:
import java.util.*;public class Solution {public List<Integer> getRow(int rowIndex) {Integer[] row = new Integer[rowIndex + 1];Arrays.fill(row, 0);row[0] = 1;for (int i = 1; i <= rowIndex; i++) {for (int j = i; j > 0; j--) {row[j] = row[j] + row[j - 1];}}return Arrays.asList(row);}
}
