小杰机器学习高级（three）——逻辑回归、二分类算法

逻辑回归与二分类

逻辑回归是分类问题，它和线性回归是不一样的。线性回归是拟合问题、预测问题，而逻辑回归，是分类问题，是二分类。

逻辑回归是一种用于解决二分类问题的机器学习算法。其原理基于线性回归模型，通过使用逻辑函数（也称为sigmoid函数）将线性回归的结果映射到一个0到1之间的概率值，从而进行分类。

1.1 散点输入

在本实验中，给出了如下两类散点，其分布如下图所示：

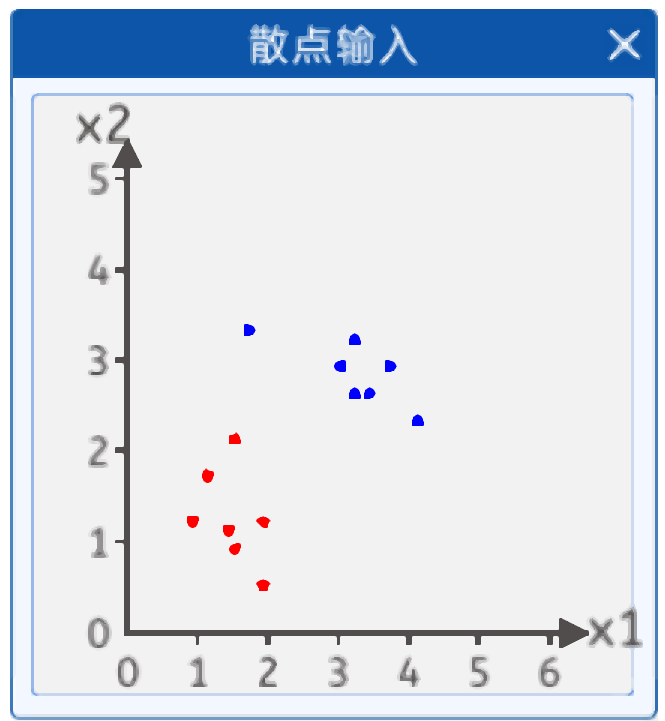
输入两个值，一个是x1 ,x2 输出是两类一类是红色点，一个是蓝色点。

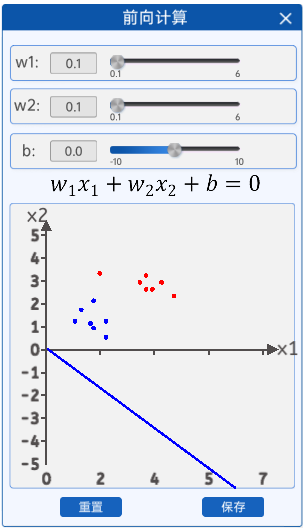
1.2 前向计算

1.3 Sigmoid函数引入

确定好线性函数公式之后，二分类的激活函数可以用Sigmoid和Softmax,这里使用Sigmoid函数作为它的输出。

如下图所示。

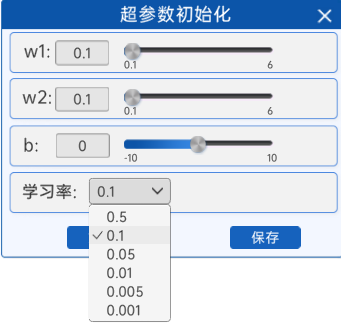
1.4 参数初始化

在“参数初始化”组件中，可以初始化两个输入特征、以及偏置b，还有学习率。由于输入特征的增加，并且使用了激活函数激活，这里的学习率会比较大一点。

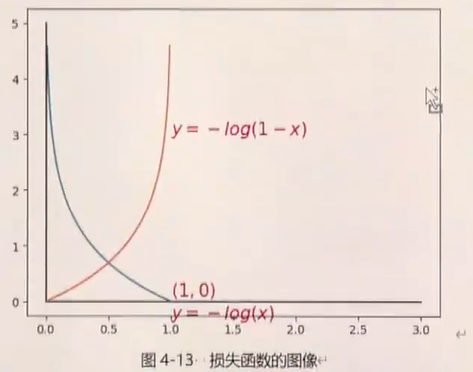
1.5 损失函数

在本实验中，选用交叉熵损失函数作为损失函数。因为交叉熵比均方差更适合分类问题，而均方差比交叉熵更适合回归问题。

在上一章节中，得到了交叉熵的表达式为：

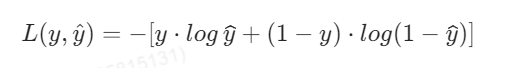
将其激活后的函数带入交叉熵中，得到：

wx+b能得到一个数值，这个数值经过Sigmoid就变成了概率，带入交叉熵损失就能计算了。

1.6 开始迭代

反向传播开始前，需要设置好迭代次数，本实验提供了“开始迭代”组件，用来设置迭代次数，次数越高，模型的效果就越好。

1.7 反向传播

接下来就是反向传播的过程，其中参数的更新同样使用的是梯度下降，也就意味着要令损失函数对参数进行求导，其结果如下图所示：

推导一下

通过“显示频率设置”组件设置迭代过程中的每迭代多少次显示一次参数值和损失值。

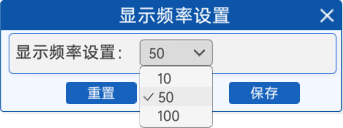
1.9 梯度下降显示

接着通过“梯度下降显示”组件显示迭代过程中返回的参数值和损失值，该组件的内容如下图所示：

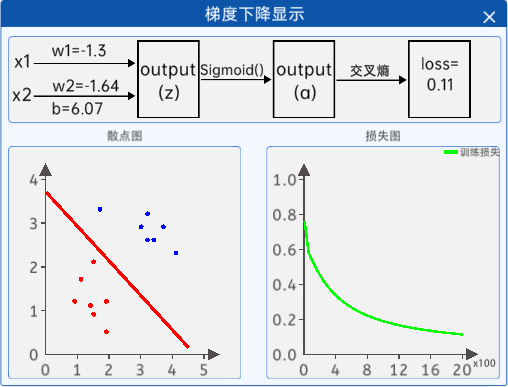
迭代完成后，我们就可以通过这个模型来预测未知的数据属于哪一类了。

标签为1和标签为0损失是怎么随着概率变化的？

不包含画图的训练代码

import numpy as np# 1.散点输入
class1_points=np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])
class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])
# 提取两类特征，输入特征维度为2
x1_data=np.concatenate((class1_points[:,0],class2_points[:,0]),axis=0)
x2_data=np.concatenate((class1_points[:,1],class2_points[:,1]),axis=0)
label=np.concatenate((np.zeros(len(class1_points)),np.ones(len(class2_points))),axis=0)
print(f"x1_data",x1_data)
print(f"x2_data",x2_data)
print(f"label",label)# 3.sigmoid 函数
def sigmoid(x):return 1 / (1 + np.exp(-x))# 2.前向计算
def forward(w1,w2,b):z=w1*x1_data+w2*x2_data+ba=sigmoid(z)return a
# 4.参数初始化
w1=0.1
w2=0.1
b=0
lr=0.05
# 5.损失函数
def loss_func(a):# 对于加和和平均 并且前面加一个负号loss=-np.mean(label*np.log(a)+(1-label)*np.log(1-a))return loss
# 6开始迭代
epoches=1000
for epoch in range(1,epoches+1):a = forward(w1, w2, b)loss=loss_func(a)#反向传播deda = (a - label) / (a * (1 - a))dadz = a * (1 - a)dzdw1 = x1_datadzw2 = x2_datadzdb = 1# 求解梯度# 数学中点积也就是内积，是指两个向量各自对应位相乘后求和# 梯度求平均防止受样本数量的影响gradient_w1=np.dot(dzdw1,deda*dadz)/(len(x1_data))gradient_w2 = np.dot(dzw2, (deda * dadz)) / (len(x2_data))gradient_b = np.mean(deda * dadz * dzdb)# 梯度更新w1= w1-lr * gradient_w1w2 = w2 - lr * gradient_w2b = b - lr * gradient_bprint(loss)

画图程序

import numpy as np
import matplotlib.pyplot as plt# 1.散点输入
class1_points = np.array([[1.9, 1.2],[1.5, 2.1],[1.9, 0.5],[1.5, 0.9],[0.9, 1.2],[1.1, 1.7],[1.4, 1.1]])class2_points = np.array([[3.2, 3.2],[3.7, 2.9],[3.2, 2.6],[1.7, 3.3],[3.4, 2.6],[4.1, 2.3],[3.0, 2.9]])
# 提取两类特征，输入特征维度为2
x1_data=np.concatenate((class1_points[:,0],class2_points[:,0]),axis=0)
x2_data=np.concatenate((class1_points[:,1],class2_points[:,1]),axis=0)
label=np.concatenate((np.zeros(len(class1_points)),np.ones(len(class2_points))),axis=0)# 2.前向计算
def forward(w1,w2,b):z=w1*x1_data+w2*x2_data+ba=sigmoid(z)return a
# 3.sigmoid 函数
def sigmoid(x):return 1/(1+np.exp(-x))
# 4.参数初始化
w1=0.1
w2=0.1
b=0
lr=0.05
# 5.损失函数
def loss_func(a):loss=-np.mean(label*np.log(a)+(1-label)*np.log(1-a))#对于加和和平均 并且前面加一个负号return loss
#画图的使用 得到画板
fig,(ax1,ax2)=plt.subplots(2,1)#添加存loss 和迭代次数的列表
loss_list=[]
epoch_list=[]
# 6开始迭代
epoches=1000
for epoch in range(1,epoches+1):# 7反向传播a=forward(w1,w2,b)deda=(a-label)/(a*(1-a))dadz=a*(1-a)dzdw1=x1_datadzw2=x2_datadzdb=1#求解梯度# 数学中点积也就是内积，是指两个向量各自对应位相乘后求和# 梯度求平均防止受样本数量的影响gradient_w1=np.dot(dzdw1,(deda*dadz))/(len(x1_data))gradient_w2 = np.dot(dzw2, (deda * dadz)) / (len(x2_data))gradient_b=np.mean(deda * dadz*dzdb)#梯度更新w1-=lr*gradient_w1w2 -= lr * gradient_w2b -= lr * gradient_b# 8显示频率设置if epoch%50==0 or epoch==1:#计算损失a=forward(w1,w2,b)loss=loss_func(a)loss_list.append(loss)epoch_list.append(epoch)print(loss)# 9.梯度下降显示#     画左图#     画左图的分割线(决策边界)#     y_hat=sigmod(w1*x1+w2*x2+b)#       使用sigmoid分两类是不是在0.5处分割，大于0.5为1 小于0.5为0#     是不是就要求w1*x1+w2*x2+b=0，因为w1*x1+w2*x2+b=0时y_hat等于0.5x1_min=x1_data.min()x1_max=x1_data.max()x2_min=-(w1*x1_min+b)/w2x2_max = -(w1 * x1_max + b)/w2#绘制散点图和决策边界#先清空图ax1.clear()#画class1_points 的点ax1.scatter(x1_data[:len(class1_points)],x2_data[:len(class2_points)],color='r')ax1.scatter(x1_data[len(class1_points):],x2_data[len(class2_points):],color='b')#画线ax1.plot([x1_min,x1_max],[x2_min,x2_max],color='r')#画右边的图ax2.clear()ax2.plot(epoch_list,loss_list)plt.pause(1)
plt.show()