在排序数组中查找元素的第一个和最后一个位置

目录

一：题目链接

二：题目思路

三：代码实现

---

一：题目链接

        题目给出的非递减顺序排列的数组，指的是整段数组要么是全部递增，或者整段数组元素大小不变，或者整段数组递增和元素大小不变区间交替。并且题目要求使用的算法时间复杂度是O(log n)，所以目前我们只能使用 二分查找 算法了。

二：题目思路

        首先，我们知道，二分查找算法 有 循环条件 和 判断条件，并且解题时我们能把数组分段来解决问题，那么就基本可以使用二分查找算法了。

        目前我们使用二分查找算法  循环条件 和 判断条件 只能找到精确的一个确定值，但是这道题结果是一个区间，所以，我们要找到左端点和右端点，那么，判断条件应该怎么改？如图：

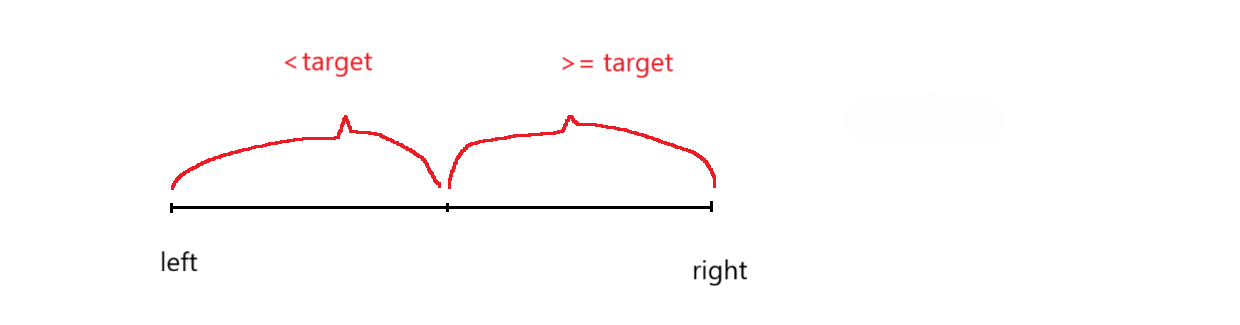
        首先，我们要找到左端点，取到 left 和 right 中点的 mid 有两种情况，可以把数组分为上图的两段。

        当 mid < target 时，证明 mid 左边一段都是 小于 target 的，那么 left 可以更新成 mid + 1。

        当 mid >= target 时，证明 mid 右边的一段是 大于或等于 target 的，此时，把 right 更新成 mid 位置，为什么 right 不更新成 mid - 1，如果 mid 的位置的值刚好是 target 起始端点，那么 right 更新成 mid - 1就会出现 left 和 right 包含的区间都是小于 target ，后续都是错误了。

        找右端点同理，取到 left 和 right 中点的 mid 有两种情况，可以把数组分为下图的两段。

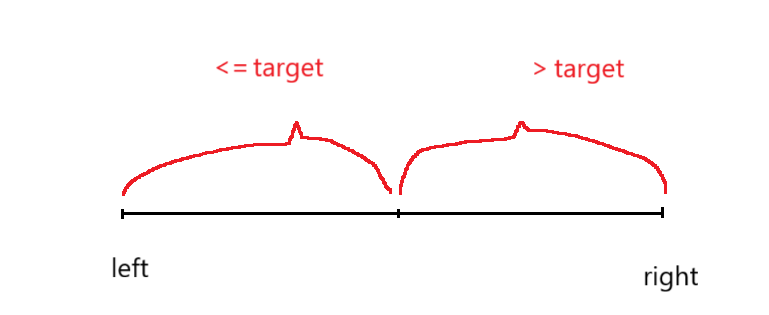
         当 mid > target 时，证明 mid 右边一段都是 大于 target 的，那么 right 可以更新成 mid - 1了。

        当 mid <= target 时，证明 mid 左边的一段是 小于或等于 target 的，此时，把 left 更新成 mid 位置，为什么 left 不更新成 mid + 1，如果 mid 的位置的值刚好是 target 结束端点，那么 left 更新成 mid + 1就会出现 left 和 right 包含的区间都是大于 target ，后续都是错误了。

解决完判断条件，那么整个判断应该在什么样的循环条件下进行？

        我们想到的肯定是 left < right ，这种循环条件一定是正确的，要不要加上 == 变成 left <= right ？我们来判断一下，如果 left == right 是什么情况？肯定是找到了当前的端点了，就可以直接返回了，如果继续循环一次，进入的是 right = mid 或者 left = mid 的判断条件，就会进入死循环了。所以，正确循环条件是 left < right 。

三：代码实现

        int[] arr = new int[2];arr[0] = -1;arr[1] = -1;//如果数组为空，直接返回if(nums.length == 0) {return arr;}//寻找左端点int left = 0;int right = nums.length - 1;while(left < right) {int mid = left + (right - left) / 2;if(nums[mid] < target) {left = mid + 1;}else {right = mid;}}//判断是否有结果if(nums[left] != target) {return arr;}arr[0] = left;//寻找右端点left = 0;right = nums.length - 1;while(left < right) {int mid = left + (right -left + 1) / 2;if(nums[mid] > target) {right = mid - 1;}else {left = mid;}}arr[1] = left;return arr;

     int mid = left + (right -left + 1) / 2；为什么找中点时里面要加一，如图：

        

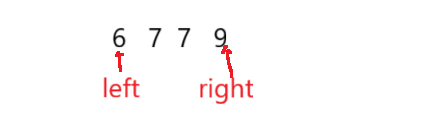
        如果 target 是 7 ，我们要找右端点时，正常来说如果代码不加一 计算的 mid 是第一个 7， 加一之后 计算的 mid 就可以取到 第二个 7 ，也就是得到右端点了。