构建AI智能体：三十八、告别“冷启动”：看大模型如何解决推荐系统的世纪难题

一、什么是协同过滤

        协同过滤是推荐系统领域最为经典和广泛应用的技术之一，其基本思想源于我们日常生活中的决策方式。当人们面临选择时，往往会参考与自己品味或需求相似的其他人的意见。比如选择餐厅时，我们会相信美食家的推荐；选购书籍时，我们会关注与自己阅读兴趣相近的朋友的书单。协同过滤正是将这种社会化的决策过程数字化和自动化。

        协同过滤基于一个核心假设：用户偏好具有持久性，过去有相似偏好的用户在未来也会表现出相似的偏好。这个假设虽然简单，但在大多数场景下都被证明是有效的。协同过滤的核心思想可以用一句话概括：物以类聚，人以群分。它不需要了解物品的任何属性信息，仅依靠用户与物品的交互历史（如评分、购买、点击等）发现用户或物品之间的相似性，从而预测用户可能喜欢的内容，就能产生推荐，与基于物品本身属性（如电影类型、商品类别）的推荐不同，协同过滤完全依赖于用户的实际行为，不需要对物品内容进行复杂理解。

协同过滤简单理解：

• 协同：多个用户共同参与数据贡献，系统利用群体智慧进行推荐
• 过滤：从海量信息中筛选出用户潜在感兴趣的内容

二、协同过滤的工作原理

工作原理可以分解为三个基本步骤：

• 首先是模式发现，系统分析所有用户的历史行为数据，寻找用户之间或物品之间的相似性模式；
• 其次是邻居形成，针对目标用户或目标物品，找到最相似的若干用户或物品；
• 最后是预测生成，基于邻居的行为预测目标用户对未知物品的偏好程度。

        这种方法的优势在于其直观性和有效性。它不需要领域专业知识，能够发现复杂的、非直观的关联关系。例如，协同过滤可能会发现喜欢购买咖啡机的人往往也喜欢购买特定品牌的咖啡豆，这种关联可能连商家自己都没有意识到。

三、相似度计算方法与细节

        相似度计算是协同过滤的核心技术环节，其准确性直接影响到推荐系统的效果。不同的相似度度量方法从不同角度衡量用户或物品之间的相似性，各有其适用场景和特点。

1. 余弦相似度

        余弦相似度是一种衡量两个向量方向相似程度的度量方法，它将用户评分看作向量空间中的向量，并通过计算两个向量夹角的余弦值来评估它们的相似性。

        它的取值范围在-1到1之间，值越接近1表示两个向量越相似，值越接近-1表示两个向量越相反，值为0表示两个向量正交，没有关联。

        在协同过滤中，我们可以把每个用户看作一个高维空间中的向量，每个维度代表一个物品的评分。余弦相似度帮助我们找到方向相似的用户，即品味相似的用户。余弦相似度的优点是不受向量长度影响，只关注方向，适合处理用户评分尺度不一致的情况。

直观理解：

• 两个指向相同方向的向量：夹角为0°，余弦值为1（完全相似）
• 两个垂直的向量：夹角为90°，余弦值为0（不相关）
• 两个指向相反方向的向量：夹角为180°，余弦值为-1（完全相反）

计算公式：

其中：

• A⋅B 是向量A和B的点积
• ∥A∥∥B∥分别是向量A和B的模（长度）

基础示例：简单二维向量

        假设有两个向量： 向量A = [3, 4]  向量B = [1, 2]

计算过程推理：

• 点积：A·B = 3×1 + 4×2 = 3 + 8 = 11
• 模长：‖A‖ = √(3² + 4²) = √(9 + 16) = √25 = 5
• 模长：‖B‖ = √(1² + 2²) = √(1 + 4) = √5 ≈ 2.236
• 余弦相似度：11 / (5 × 2.236) ≈ 11 / 11.18 ≈ 0.984

用户示例：用户评分向量

        假设两个用户对三部电影的评分：

• 用户A: [5, 3, 0]（给电影1评5分，电影2评3分，没看过电影3）
• 用户B: [4, 2, 5]（给电影1评4分，电影2评2分，电影3评5分）

计算过程推理：

• 点积：A·B = 5×4 + 3×2 + 0×5 = 20 + 6 + 0 = 26
• 模长：‖A‖ = √(5² + 3² + 0²) = √(25 + 9 + 0) = √34 ≈ 5.831
• 模长：‖B‖ = √(4² + 2² + 5²) = √(16 + 4 + 25) = √45 ≈ 6.708
• 余弦相似度：26 / (5.831 × 6.708) ≈ 26 / 39.11 ≈ 0.665

代码演示：

import numpy as npdef cosine_similarity_basic(vec_a, vec_b):"""计算两个向量的余弦相似度参数:vec_a: 第一个向量vec_b: 第二个向量返回:余弦相似度值"""# 转换为numpy数组a = np.array(vec_a)b = np.array(vec_b)# 计算点积dot_product = np.dot(a, b)# 计算模长norm_a = np.linalg.norm(a)norm_b = np.linalg.norm(b)# 计算余弦相似度if norm_a == 0 or norm_b == 0:return 0  # 避免除以零return dot_product / (norm_a * norm_b)# 测试
vector1 = [3, 4]
vector2 = [1, 2]
similarity = cosine_similarity_basic(vector1, vector2)
print(f"向量{vector1}和{vector2}的余弦相似度: {similarity:.3f}")# 用户评分示例
user_a = [5, 3, 0]
user_b = [4, 2, 5]
user_similarity = cosine_similarity_basic(user_a, user_b)
print(f"用户A{user_a}和用户B{user_b}的余弦相似度: {user_similarity:.3f}")

输出结果：

向量[3, 4]和[1, 2]的余弦相似度: 0.984
用户A[5, 3, 0]和用户B[4, 2, 5]的余弦相似度: 0.665

2. 皮尔逊相关系数

        皮尔逊相关系数衡量的是两个变量之间的线性相关程度。在协同过滤中，它测量的是两个用户评分模式的一致性，而不是评分的绝对值。皮尔逊相关系数的取值范围也是[-1, 1]，正值表示正相关，负值表示负相关。

        与余弦相似度不同，皮尔逊相关系数考虑了用户平均评分的影响，因此能够缓解用户评分严格度不同带来的偏差，能更准确地反映用户品味的相似性。例如，有些用户习惯打高分，有些用户习惯打低分，皮尔逊相关系数能够消除这种个体差异的影响。

计算公式：

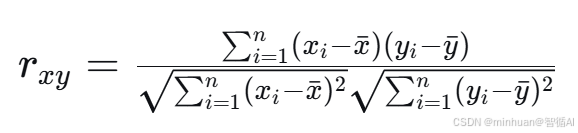
其中：

• $x_i$ 和 $y_i$ 分别是两个用户对同一物品的评分
• $\bar{x}$ 和 $\bar{y}$ 分别是两个用户的平均评分
• $n$ 是两个用户共同评分的物品数量

取值范围和解释：

• r = 1：完全正相关
• r = -1：完全负相关
• r = 0：无线性相关
• 0 < r < 1：正相关（越接近1相关性越强）
• -1 < r < 0：负相关（越接近-1负相关性越强）

评分过程推理：

假设我们有两个用户（用户A和用户B）对5部电影的评分情况：

电影	用户A评分	用户B评分
电影1	5	4
电影2	4	5
电影3	3	2
电影4	2	1
电影5	1	3

第一步：计算平均评分

首先计算每个用户的平均评分：

• 用户A的平均评分：(5 + 4 + 3 + 2 + 1)/5 = 3
• 用户B的平均评分：(4 + 5 + 2 + 1 + 3)/5 = 3

第二步：计算评分与平均分的差值

计算每个评分与其相应用户平均分的差值：

电影	用户A评分	用户B评分	A评分差值	B评分差值
电影1	5	4	5-3 = 2	4-3 = 1
电影2	4	5	4-3 = 1	5-3 = 2
电影3	3	2	3-3 = 0	2-3 = -1
电影4	2	1	2-3 = -1	1-3 = -2
电影5	1	3	1-3 = -2	3-3 = 0

第三步：计算分子部分

计算分子：每部电影的差值的乘积之和

电影	A评分差值	B评分差值	乘积
电影1	2	1	2×1 = 2
电影2	1	2	1×2 = 2
电影3	0	-1	0×(-1) = 0
电影4	-1	-2	(-1)×(-2) = 2
电影5	-2	0	(-2)×0 = 0

分子总和 = 2 + 2 + 0 + 2 + 0 = 6

第四步：计算分母部分

分母由两部分组成：

第一部分：取A用户评分差值的平方之和的平方跟

电影	A评分差值	A差值的平方
电影1	2	4
电影2	1	1
电影3	0	0
电影4	-1	1
电影5	-2	4

总和 = 4 + 1 + 0 + 1 + 4 = 10
平方根 = √10 ≈ 3.162 （√为平方根符号）

第二部分：取B用户评分差值的平方之和的平方跟

电影	B评分差值	B差值的平方
电影1	1	1
电影2	2	4
电影3	-1	1
电影4	-2	4
电影5	0	0

总和 = 1 + 4 + 1 + 4 + 0 = 10
平方根 = √10 ≈ 3.162 （√为平方根符号）
分母 = 3.162 × 3.162 = 10.000

第五步：计算皮尔逊相关系数

现在我们可以计算最终的皮尔逊相关系数：

r= 分子/分母 = 6/10 = 0.6

结果评估：

• 正相关：用户A和用户B的评分模式呈现正相关关系
• 中等强度：0.6的相关性表明两个用户的品味有中等程度的相似性
• 一致性：当用户A给某部电影评分高于其平均水平时，用户B也倾向于给这部电影评分高于其平均水平

与余弦相似度的对比

为了对比，我们计算一下相同数据的余弦相似度：

余弦相似度计算：

• 分子：5×4 + 4×5 + 3×2 + 2×1 + 1×3 = 20 + 20 + 6 + 2 + 3 = 51
• 分母：√(5²+4²+3²+2²+1²) × √(4²+5²+2²+1²+3²) = √(25+16+9+4+1) × √(16+25+4+1+9) = √55 × √55 = 7.416 × 7.416 = 55
• 余弦相似度：51/55 ≈ 0.927

对比分析：

• 余弦相似度：0.927（非常高）
• 皮尔逊相关系数：0.6（中等）

差异原因：

        因为余弦相似度没有考虑用户的平均评分习惯。用户A和用户B的平均评分都是3，但他们的评分模式有所不同。皮尔逊相关系数通过中心化处理，更好地反映了评分模式的一致性。

代码示例：

import numpy as np
from scipy.stats import pearsonr# 用户评分数据
userA_ratings = [5, 4, 3, 2, 1]
userB_ratings = [4, 5, 2, 1, 3]# 手动计算皮尔逊相关系数
def manual_pearson(x, y):# 计算平均值mean_x = np.mean(x)mean_y = np.mean(y)# 计算分子numerator = np.sum((np.array(x) - mean_x) * (np.array(y) - mean_y))# 计算分母denominator = np.sqrt(np.sum((np.array(x) - mean_x)**2)) * np.sqrt(np.sum((np.array(y) - mean_y)**2))return numerator / denominator# 使用scipy计算
scipy_pearson, _ = pearsonr(userA_ratings, userB_ratings)print(f"手动计算皮尔逊系数: {manual_pearson(userA_ratings, userB_ratings):.3f}")
print(f"Scipy计算皮尔逊系数: {scipy_pearson:.3f}")# 计算余弦相似度
from sklearn.metrics.pairwise import cosine_similarity
cosine_sim = cosine_similarity([userA_ratings], [userB_ratings])[0][0]
print(f"余弦相似度: {cosine_sim:.3f}")

输出结果：

手动计算皮尔逊系数: 0.600
Scipy计算皮尔逊系数: 0.600
余弦相似度: 0.927​

3. 调整余弦相似度

        调整余弦相似度是针对余弦相似度的改进版本，它从每个评分中减去相应用户的平均评分，从而消除用户评分偏差。这是因为不同的用户可能有不同的评分习惯：有些用户倾向于打高分，有些用户则倾向于打低分。这种方法结合了余弦相似度和皮尔逊相关系数的优点，在实践中表现出更好的性能。

计算公式：

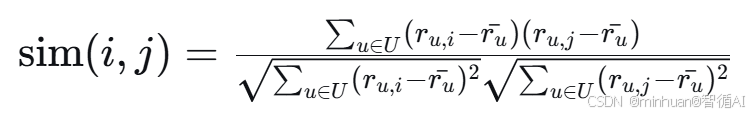
其中：

• $r_{u,i}$ 是用户 $u$ 对物品 $i$ 的评分
• $r_{u,j}$ 是用户 $u$ 对物品 $j$ 的评分
• $\bar{r_u}$ 是用户 $u$ 的平均评分
• $U$ 是同时对物品 $i$ 和 $j$ 评分的用户集合

评分过程推理：

假设我们有3个用户对3个物品的评分：

用户	物品A	物品B	物品C	平均分
用户1	5	3	2	3.33
用户2	4	2	1	2.33
用户3	3	4	5	4.00

计算物品A和物品B的调整余弦相似度

第一步: 计算调整后的评分

• 用户1: (5-3.33, 3-3.33) = (1.67, -0.33)
• 用户2: (4-2.33, 2-2.33) = (1.67, -0.33)
• 用户3: (3-4.00, 4-4.00) = (-1.00, 0.00)

第二步: 计算分子

• 分子 = (1.67)(-0.33) + (1.67)(-0.33) + (-1.00)(0.00) = -0.55 - 0.55 + 0 = -1.10

第三步: 计算分母

• 分母A = √(1.67² + 1.67² + (-1.00)²) = √(2.79 + 2.79 + 1.00) = √6.58 = 2.57
• 分母B = √((-0.33)² + (-0.33)² + 0.00²) = √(0.11 + 0.11 + 0.00) = √0.22 = 0.47

第四步: 计算相似度

• 相似度 = -1.10 / (2.57 × 0.47) = -1.10 / 1.21 ≈ -0.91

代码示例：

import numpy as np
import pandas as pddef adjusted_cosine_similarity(item_i_ratings, item_j_ratings, user_means):"""计算两个物品之间的调整余弦相似度参数:item_i_ratings: 物品i的评分列表item_j_ratings: 物品j的评分列表  user_means: 相应用户的平均评分列表返回:调整余弦相似度"""# 转换为numpy数组ratings_i = np.array(item_i_ratings)ratings_j = np.array(item_j_ratings)means = np.array(user_means)# 只考虑两个物品都被评分的用户common_ratings = np.where((ratings_i > 0) & (ratings_j > 0))[0]if len(common_ratings) < 2:return 0  # 需要至少2个共同评分用户ratings_i_common = ratings_i[common_ratings]ratings_j_common = ratings_j[common_ratings]means_common = means[common_ratings]# 计算调整后的评分adjusted_i = ratings_i_common - means_commonadjusted_j = ratings_j_common - means_common# 计算分子和分母numerator = np.sum(adjusted_i * adjusted_j)denominator = np.sqrt(np.sum(adjusted_i**2)) * np.sqrt(np.sum(adjusted_j**2))# 避免除以零if denominator == 0:return 0return numerator / denominator# 示例使用
itemA_ratings = [5, 4, 3]  # 三个用户对物品A的评分
itemB_ratings = [3, 2, 4]  # 三个用户对物品B的评分
user_means = [3.33, 2.33, 4.00]  # 三个用户的平均评分
# 计算余弦相似度
from sklearn.metrics.pairwise import cosine_similarity
cosine_sim = cosine_similarity([itemA_ratings], [itemB_ratings])[0][0]
print(f"余弦相似度: {cosine_sim:.3f}")
adj_cosine_sim = adjusted_cosine_similarity(itemA_ratings, itemB_ratings, user_means)
print(f"调整余弦相似度: {adj_cosine_sim:.3f}")

输出结果：

余弦相似度: 0.919
调整余弦相似度: -0.921

        通过结果看出两中评分的差异还是很大的，调整余弦相似度就是要消除评分偏差，比传统余弦相似度更能反映物品之间的真实相似性，特别适合物品数量少于用户数量的场景。

四、协同过滤的两种核心类型

        协同过滤主要分为两大类型：基于内存的方法和基于模型的方法。基于内存的方法直接使用整个用户-物品交互数据集进行预测，而基于模型的方法则先从数据中学习一个预测模型，再用这个模型进行预测。

1. 基于内存的方法

1.1 基于用户的协同过滤

• 核心逻辑：找到与目标用户兴趣相似的用户群体，然后基于这个群体的偏好来预测目标用户可能喜欢的物品。
• 方法说明：这种方法依赖于用户间的相似度计算，用户相似度计算后，选择最相似的K个用户作为邻居，然后基于邻居用户的评分进行加权平均来预测目标用户对未知物品的评分。

生活化例子：

        假设你和朋友小明都喜欢《星际穿越》《盗梦空间》《信条》这三部诺兰电影，且都打了5星。系统发现你们的观影偏好高度相似（相似度90%），而小明最近给《变形金刚》打了5星，那么系统就会把《变形金刚》推荐给你。

实现步骤：

第一步：构建用户-物品评分矩阵

假设有3个用户和4部电影，评分范围1-5（0表示未评分）：

用户/电影	星际穿越	盗梦空间	信条	变形金刚
你	5	5	5	0
小明	5	4	5	5
小红	2	3	2	0

第二步：计算用户相似度

        系统会对比你和其他用户的评分向量，计算“相似度分数”。最常用的方法是余弦相似度，可以理解为“两个用户偏好向量之间的夹角大小”——夹角越小，偏好越相似。

        在上面的例子中，你和小明的相似度远高于你和小红（接近90% vs 约30%）。

第三步：找到邻居用户并生成推荐

        选择与你最相似的K个用户（比如K=10），将他们喜欢但你未评分的物品，按相似度加权平均后推荐给你。

示例：计算用户相似度矩阵

def calculate_pearson_similarity_matrix(ratings_df):"""计算所有用户之间的皮尔逊相关系数矩阵参数:ratings_df: 用户-物品评分DataFrame返回:皮尔逊相似度矩阵DataFrame"""n_users = ratings_df.shape[1]  # 用户数量similarity_matrix = np.zeros((n_users, n_users))# 获取用户列表users = ratings_df.columns.tolist()# 计算每对用户之间的相似度for i in range(n_users):for j in range(i, n_users):  # 只需计算上三角矩阵if i == j:similarity_matrix[i, j] = 1.0  # 用户与自己的相似度为1else:user_i_ratings = ratings_df[users[i]].valuesuser_j_ratings = ratings_df[users[j]].valuessimilarity = pearson_similarity(user_i_ratings, user_j_ratings)similarity_matrix[i, j] = similaritysimilarity_matrix[j, i] = similarity  # 对称矩阵# 转换为DataFramesimilarity_df = pd.DataFrame(similarity_matrix,index=users,columns=users)return similarity_df# 创建示例数据
ratings_data = {'用户1': [5, 4, 0, 0, 3],'用户2': [4, 0, 5, 0, 2],'用户3': [0, 3, 4, 5, 0],'用户4': [2, 0, 0, 4, 5],'用户5': [0, 5, 3, 0, 4]
}
movies = ['电影A', '电影B', '电影C', '电影D', '电影E']ratings_df = pd.DataFrame(ratings_data, index=movies)# 计算皮尔逊相似度矩阵
pearson_sim_df = calculate_pearson_similarity_matrix(ratings_df)
print("皮尔逊相似度矩阵:")
print(pearson_sim_df)

输出结果：

皮尔逊相似度矩阵:
用户1  用户2  用户3  用户4  用户5
用户1  1.0  1.0  0.0 -1.0  1.0        
用户2  1.0  1.0  0.0 -1.0 -1.0        
用户3  0.0  0.0  1.0  0.0 -1.0
用户4 -1.0 -1.0  0.0  1.0  0.0
用户5  1.0 -1.0 -1.0  0.0  1.0

1.2 基于物品的协同过滤

• 核心逻辑：首先计算物品之间的相似度，然后根据用户历史喜欢的物品找到相似物品进行推荐。
• 方法说明：这种方法的基本假设是，如果用户喜欢某个物品，那么他也很可能喜欢与这个物品相似的其他物品。基于物品的方法在实际应用中往往表现更好，因为物品之间的关系通常比用户之间的关系更加稳定，而且物品的数量通常少于用户数量，计算效率更高。

生活化例子：

        如果你买了《哈利波特与魔法石》，电商平台会推荐《哈利波特与密室》。这不是因为系统知道它们都是“奇幻小说”（基于内容的推荐），而是因为数据显示：购买《魔法石》的用户中，有80%也会购买《密室》——系统通过用户行为发现了物品之间的隐藏关联。

实现步骤：

第一步：构建物品-用户评分矩阵

以电影为行，用户为列：

电影	你	小明	小红
星际穿越	5	5	2
盗梦空间	5	4	3
信条	5	5	2
变形金刚	0	5	0

第二步：计算物品相似度

        分析哪些电影经常被同一批用户喜欢。例如，《星际穿越》和《信条》的评分向量高度相似（你和小明都打了5星，小红打了2星），因此它们的相似度很高。

第三步：生成推荐

        对于你喜欢的电影（如《星际穿越》），找出与其最相似的K部电影（如《信条》《奥本海默》），推荐给你。
示例：计算物品相似度矩阵

def calculate_adjusted_cosine_matrix(ratings_df):"""计算所有物品之间的调整余弦相似度矩阵参数:ratings_df: 用户-物品评分DataFrame（行:物品, 列:用户）返回:调整余弦相似度矩阵"""n_items = ratings_df.shape[0]  # 物品数量items = ratings_df.index.tolist()# 计算每个用户的平均评分user_means = ratings_df.mean(axis=0)# 初始化相似度矩阵similarity_matrix = np.zeros((n_items, n_items))# 计算每对物品之间的相似度for i in range(n_items):for j in range(i, n_items):  # 只需计算上三角矩阵if i == j:similarity_matrix[i, j] = 1.0  # 物品与自身的相似度为1else:item_i_ratings = ratings_df.iloc[i].valuesitem_j_ratings = ratings_df.iloc[j].valuessim = adjusted_cosine_similarity(item_i_ratings, item_j_ratings, user_means.values)similarity_matrix[i, j] = simsimilarity_matrix[j, i] = sim  # 对称矩阵# 转换为DataFramesimilarity_df = pd.DataFrame(similarity_matrix,index=items,columns=items)return similarity_df# 创建示例数据
ratings_data = {'用户1': [5, 4, 0, 0, 3],'用户2': [4, 0, 5, 0, 2], '用户3': [0, 3, 4, 5, 0],'用户4': [2, 0, 0, 4, 5],'用户5': [0, 5, 3, 0, 4]
}
movies = ['电影A', '电影B', '电影C', '电影D', '电影E']ratings_df = pd.DataFrame(ratings_data, index=movies)# 计算调整余弦相似度矩阵
adj_cosine_sim_df = calculate_adjusted_cosine_matrix(ratings_df)
print("调整余弦相似度矩阵:")
print(adj_cosine_sim_df)

输出结果：

物品调整余弦相似度矩阵:
电影A       电影B       电影C  电影D       电影E
电影A  1.000000  0.000000  0.000000  0.0  0.070364
电影B  0.000000  1.000000  0.552674  0.0  0.981455
电影C  0.000000  0.552674  1.000000  0.0  0.086630
电影D  0.000000  0.000000  0.000000  1.0  0.000000
电影E  0.070364  0.981455  0.086630  0.0  1.000000

1.3 两者的关键区别

维度	基于用户的协同过滤	基于物品的协同过滤
核心对象	用户相似度	物品相似度
适用场景	用户少、物品多（如小众社区）	物品少、用户多（如电商平台）
稳定性	较差（用户偏好易变化）	较好（物品属性相对稳定）
推荐解释性	难（“和你相似的人喜欢”）	易（“你喜欢的物品类似”）
计算复杂度	高（用户增长快）	低（物品更新慢）

2. 基于模型的方法

        通过机器学习算法从数据中学习一个预测模型。常见的模型包括矩阵分解、聚类模型、深度学习模型等。其中，矩阵分解是最为经典的模型方法，它将用户-物品评分矩阵分解为用户特征矩阵和物品特征矩阵的乘积，通过潜在特征向量来表示用户和物品。

        大模型的结合可以很好的解决新用户或新物品缺乏历史数据的问题，也正好解决了疑难的冷启动的问题。

示例：基于大语言模型的混合推荐系统

        示例结合了传统的协同过滤方法和现代的大语言模型技术。系统首先使用传统的用户-物品评分矩阵，然后通过大语言模型分析物品的文本描述来计算语义相似度，最终将两种相似度结合来生成更准确的推荐。

2.1 代码结构

2.1.1 数据准备

# 创建示例数据：用户对电影的评分
# 行代表用户，列代表电影，数值代表评分（0表示未评分）
ratings_data = {'用户1': [5, 4, 3, 0, 0],'用户2': [4, 5, 0, 2, 1],'用户3': [3, 0, 4, 5, 2],'用户4': [0, 3, 5, 4, 3],'用户5': [2, 1, 0, 3, 4]
}
movies = ['电影A', '电影B', '电影C', '电影D', '电影E']# 创建评分矩阵
ratings_df = pd.DataFrame(ratings_data, index=movies)
print("用户-电影评分矩阵:")
print(ratings_df)

意图说明：

• 创建一个模拟的用户-电影评分数据集，用于演示推荐系统的工作原理
• 使用0表示用户未观看或未评分的电影，这是推荐系统中常见的表示方法
• 构建一个DataFrame结构，便于后续的数据处理和计算

2.1.2 文本相似度计算器

class TextSimilarityCalculator:"""基于大模型的文本相似度计算器"""def __init__(self, model_name='D:/modelscope/hub/models/sentence-transformers/all-MiniLM-L6-v2'):# 初始化代码...def encode_texts(self, texts):# 编码文本...def calculate_similarity(self, text1, text2):# 计算两个文本的相似度...def batch_similarity_matrix(self, texts):# 批量计算相似度矩阵...

意图说明：

• 创建一个专门用于计算文本相似度的类，封装了大语言模型的使用细节
• 使用Sentence Transformer模型将文本转换为高维向量表示
• 模型采用的本地路径，在前面的文章中，也用到了这个模型，已经下载到了本地
• 通过计算向量间的余弦相似度来量化文本之间的语义相似性
• 提供批量处理功能，提高计算效率

2.1.3 混合推荐系统

class HybridRecommender:"""结合传统协同过滤和大模型的混合推荐系统"""def __init__(self, ratings_df, text_model_name='D:/modelscope/hub/models/sentence-transformers/all-MiniLM-L6-v2'):# 初始化代码...def _precompute_item_embeddings(self):# 预计算物品嵌入...def calculate_semantic_similarity(self, item_id1, item_id2):# 计算语义相似度...def hybrid_similarity(self, item_id1, item_id2, alpha=0.7):# 计算混合相似度...def _calculate_cf_similarity(self, item_id1, item_id2):# 计算协同过滤相似度...def generate_recommendations(self, target_user_id, top_n=5, alpha=0.7):# 生成推荐...def _predict_rating(self, user_id, item_id, alpha):# 预测评分...

意图说明：

• 创于物品的协同过滤，使用皮尔逊相关系数计算物品相似度
• 提供生建一个混合推荐系统，结合传统协同过滤和大语言模型的优势
• 使用参数alpha控制两种方法的权重，实现灵活的混合策略
• 预计算物品的文本嵌入，提高推荐时的计算效率
• 实现基成推荐列表的功能，为目标用户预测对未评分物品的评分

2.2 输出结果

用户-电影评分矩阵:
用户1  用户2  用户3  用户4  用户5
电影A    5    4    3    0    2
电影B    4    5    0    3    1
电影C    3    0    4    5    0
电影D    0    2    5    4    3
电影E    0    1    2    3    4
加载模型: D:/modelscope/hub/models/sentence-transformers/all-MiniLM-L6-v2
电影描述语义相似度矩阵:
[[1.0000004  0.78310543 0.8368864  0.7532436 ]
[0.78310543 0.9999992  0.79229146 0.6913045 ]
[0.8368864  0.79229146 0.9999998  0.70960337]
[0.7532436  0.6913045  0.70960337 0.9999997 ]]

电影相似度: 0.791
加载模型: D:/modelscope/hub/models/sentence-transformers/all-MiniLM-L6-v2
推荐: 电影D, 预测评分: 2.10
推荐: 电影E, 预测评分: 1.95

2.3 核心算法

2.3.1 语义相似度计算

        系统使用大语言模型将物品的文本描述转换为高维向量，然后通过计算向量间的余弦相似度来量化物品之间的语义相似性。这种方法能够捕捉到传统协同过滤无法发现的深层语义关系。

2.3.2 混合相似度计算

        系统将传统的协同过滤相似度和大语言模型计算的语义相似度进行加权融合：

混合相似度 = α × 协同过滤相似度 + (1-α) × 语义相似度

2.3.3 评分预测

        对于目标用户未评分的物品，系统基于用户已评分的相似物品进行评分预测：

预测评分 = 用户平均评分 + ∑[相似度 × (评分 - 物品平均评分)] / ∑|相似度|

这种方法既考虑了用户的整体评分习惯，也考虑了物品的相对受欢迎程度。

2.3.4 基于大模型的相似度计算为推荐系统做了进一步的优化改进： 

• 深度语义理解：能够理解内容的深层含义，而不仅仅是表面特征
• 跨模态能力：可以处理文本、图像、音频等多种类型的数据
• 解决冷启动：有效处理新用户和新物品的推荐问题
• 增强可解释性：能够生成自然语言的推荐解释

3.  各自的适用场景

每种类型的协同过滤都有其适用场景和优缺点。

• 基于用户的方法更适用于用户群体相对稳定、用户兴趣多样性较强的场景；
• 基于物品的方法更适合物品数量相对较少、物品特征相对稳定的场景；
• 而基于模型的方法则更适合大规模数据集和需要离线训练的场景。

五、协同过滤挑战与解决方案

1. 冷启动问题

• 场景：新用户（无行为数据）、新物品（无交互记录）、新平台（无任何数据）
• 解决方法：
  • 新用户：基于注册信息（年龄、性别）或热门物品推荐
  • 新物品：基于内容特征（如电影类型、导演）或人工标注
  • 混合推荐：结合基于内容的推荐（如“你喜欢科幻片，推荐《沙丘》”）

2. 数据稀疏性

• 问题：用户-物品矩阵中99%以上的位置是0（用户很少评分）
• 解决方法：
  • 降维技术：如矩阵分解（SVD），将高维稀疏矩阵压缩为低维稠密矩阵
  • 邻居选择优化：只考虑有共同评分的用户/物品计算相似度

3. 可扩展性

• 问题：当用户或物品数量达百万级时，计算所有相似度变得极其缓慢
• 解决方法：
  • 近似算法：如局部敏感哈希（LSH）快速查找相似用户/物品
  • 离线计算：提前预计算物品相似度，实时推荐时直接查询

六、经典应用场景

• 电商平台：淘宝“猜你喜欢”、亚马逊“购买此商品的人还购买了”
• 流媒体：Netflix电影推荐、Spotify歌曲推荐
• 社交网络：Facebook好友推荐、LinkedIn职位推荐

七、总结

        协同过滤作为推荐系统的经典方法，在处理用户行为数据方面具有不可替代的价值。而大模型的出现为推荐系统带来了语义理解、内容生成和跨模态处理等新能力。两者的结合代表了推荐系统发展的新方向：

传统协同过滤的价值：

• 在处理大量用户行为数据方面仍然有效
• 算法相对简单，计算效率高
• 在实际系统中经过长期验证

大模型的贡献：

• 解决冷启动问题，处理新用户和新物品
• 提供深度语义理解和跨模态能力
• 增强推荐的可解释性和用户体验

        随着大模型技术的不断发展和优化，以及计算资源的更加普及，基于协同过滤和大模型的混合推荐系统将成为主流。这种系统不仅能够提供更准确的推荐，还能够提供更加人性化和可解释的推荐体验，真正实现懂你所需、荐你所想的个性化服务。

附录：基于模型的方法完整代码

import numpy as np
from sentence_transformers import SentenceTransformer
from sklearn.metrics.pairwise import cosine_similarity
import torch
import pandas as pd
from sklearn.metrics.pairwise import cosine_similarity# 创建示例数据：用户对电影的评分
# 行代表用户，列代表电影，数值代表评分（0表示未评分）
ratings_data = {'用户1': [5, 4, 3, 0, 0],'用户2': [4, 5, 0, 2, 1],'用户3': [3, 0, 4, 5, 2],'用户4': [0, 3, 5, 4, 3],'用户5': [2, 1, 0, 3, 4]
}
movies = ['电影A', '电影B', '电影C', '电影D', '电影E']# 创建评分矩阵
ratings_df = pd.DataFrame(ratings_data, index=movies)
print("用户-电影评分矩阵:")
print(ratings_df)
class TextSimilarityCalculator:"""基于大模型的文本相似度计算器"""def __init__(self, model_name='D:/modelscope/hub/models/sentence-transformers/all-MiniLM-L6-v2'):"""初始化文本相似度计算器参数:model_name: 预训练模型名称- 'all-MiniLM-L6-v2': 轻量级通用模型- 'all-mpnet-base-v2': 高质量通用模型  - 'multi-qa-mpnet-base-dot-v1': 问答优化模型"""self.model = SentenceTransformer(model_name)print(f"加载模型: {model_name}")def encode_texts(self, texts):"""将文本列表编码为向量表示参数:texts: 文本列表返回:文本向量矩阵"""return self.model.encode(texts, convert_to_tensor=True)def calculate_similarity(self, text1, text2):"""计算两个文本之间的相似度参数:text1: 第一个文本text2: 第二个文本返回:相似度分数 (0-1)"""# 编码文本embeddings = self.encode_texts([text1, text2])# 计算余弦相似度similarity = cosine_similarity(embeddings[0].cpu().numpy().reshape(1, -1),embeddings[1].cpu().numpy().reshape(1, -1))[0][0]return similaritydef batch_similarity_matrix(self, texts):"""计算文本集合的相似度矩阵参数:texts: 文本列表返回:相似度矩阵"""embeddings = self.encode_texts(texts)similarity_matrix = cosine_similarity(embeddings.cpu().numpy())return similarity_matrix# 使用示例
text_calculator = TextSimilarityCalculator()# 电影描述示例
movie_descriptions = ["一部讲述黑客与反乌托邦系统斗争的赛博朋克惊悚片","一部设定在未来世界、科技先进的科幻冒险片","一部讲述两人在纽约坠入爱河的浪漫喜剧","一部以二战为背景的历史剧"
]# 计算相似度矩阵
similarity_matrix = text_calculator.batch_similarity_matrix(movie_descriptions)
print("电影描述语义相似度矩阵:")
print(similarity_matrix)# 计算特定文本对相似度
text1 = "一部关于人工智能和机器人的电影"
text2 = "一部探索人类与机器之间关系的电影"
similarity = text_calculator.calculate_similarity(text1, text2)
print(f"\n电影相似度: {similarity:.3f}")
print("=" * 50)
print("混合推荐系统")
print("=" * 50)
class HybridRecommender:"""结合传统协同过滤和大模型的混合推荐系统"""def __init__(self, ratings_df, text_model_name='D:/modelscope/hub/models/sentence-transformers/all-MiniLM-L6-v2'):"""初始化混合推荐系统参数:ratings_df: 用户-物品评分DataFrametext_model_name: 文本编码模型名称"""self.ratings_df = ratings_dfself.text_calculator = TextSimilarityCalculator(text_model_name)# 预计算物品文本特征self.item_descriptions = {}  # 假设有物品描述数据self.item_embeddings = self._precompute_item_embeddings()def _precompute_item_embeddings(self):"""预计算所有物品的文本嵌入"""item_ids = self.ratings_df.index.tolist()descriptions = [self.item_descriptions.get(item_id, "") for item_id in item_ids]return self.text_calculator.encode_texts(descriptions)def calculate_semantic_similarity(self, item_id1, item_id2):"""计算两个物品的语义相似度"""idx1 = self.ratings_df.index.get_loc(item_id1)idx2 = self.ratings_df.index.get_loc(item_id2)emb1 = self.item_embeddings[idx1].cpu().numpy()emb2 = self.item_embeddings[idx2].cpu().numpy()return cosine_similarity([emb1], [emb2])[0][0]def hybrid_similarity(self, item_id1, item_id2, alpha=0.7):"""计算混合相似度（协同过滤 + 语义相似度）参数:item_id1: 物品1IDitem_id2: 物品2ID  alpha: 协同过滤权重 (1-alpha为语义相似度权重)"""# 计算传统协同过滤相似度（基于评分）cf_similarity = self._calculate_cf_similarity(item_id1, item_id2)# 计算语义相似度semantic_similarity = self.calculate_semantic_similarity(item_id1, item_id2)# 混合相似度hybrid_sim = alpha * cf_similarity + (1 - alpha) * semantic_similarityreturn hybrid_simdef _calculate_cf_similarity(self, item_id1, item_id2):"""计算基于评分的协同过滤相似度"""ratings1 = self.ratings_df.loc[item_id1].valuesratings2 = self.ratings_df.loc[item_id2].values# 只考虑共同评分的用户common_ratings = np.where((ratings1 > 0) & (ratings2 > 0))[0]if len(common_ratings) < 2:return 0# 使用皮尔逊相关系数from scipy.stats import pearsonrcorr, _ = pearsonr(ratings1[common_ratings], ratings2[common_ratings])return 0 if np.isnan(corr) else corrdef generate_recommendations(self, target_user_id, top_n=5, alpha=0.7):"""生成混合推荐"""# 获取目标用户未评分的物品user_ratings = self.ratings_df[target_user_id]unrated_items = user_ratings[user_ratings == 0].indexpredictions = []for item_id in unrated_items:# 计算预测评分predicted_rating = self._predict_rating(target_user_id, item_id, alpha)predictions.append((item_id, predicted_rating))# 返回topN推荐predictions.sort(key=lambda x: x[1], reverse=True)return predictions[:top_n]def _predict_rating(self, user_id, item_id, alpha):"""预测用户对物品的评分"""# 基于相似物品的评分进行预测user_mean = self.ratings_df[user_id].mean()numerator = 0denominator = 0# 找到用户已评分的物品rated_items = self.ratings_df[user_id][self.ratings_df[user_id] > 0].indexfor rated_item in rated_items:similarity = self.hybrid_similarity(item_id, rated_item, alpha)rating = self.ratings_df.loc[rated_item, user_id]item_mean = self.ratings_df.loc[rated_item].mean()numerator += similarity * (rating - item_mean)denominator += abs(similarity)if denominator == 0:return user_meanpredicted_rating = user_mean + (numerator / denominator)return max(1, min(5, predicted_rating))  # 确保评分在1-5范围内# 使用示例
# 假设已有ratings_df和物品描述
hybrid_rec = HybridRecommender(ratings_df)
recommendations = hybrid_rec.generate_recommendations('用户1')
for item_id, rating in recommendations:print(f"推荐: {item_id}, 预测评分: {rating:.2f}")