陈童理论物理新讲1 哈密顿力学初步

本博客会默认读者有高中物理基础

势能与力

能量与力

我们通过势能（与位置有关的能量）来定义力：

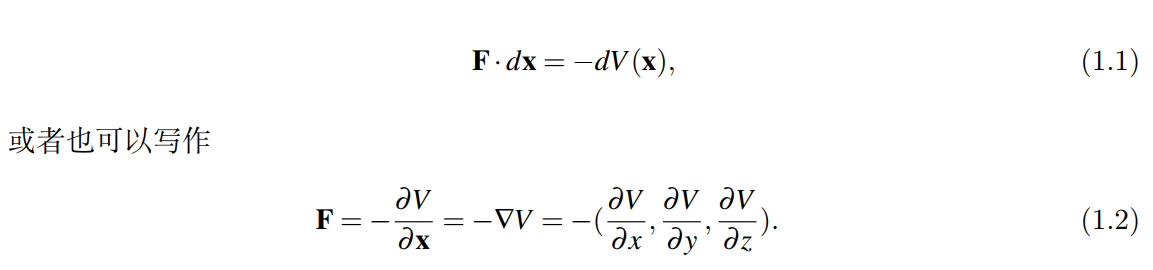
力是势能关于位置的变化量。

哈密顿正则方程

我们重写牛顿运动定律：

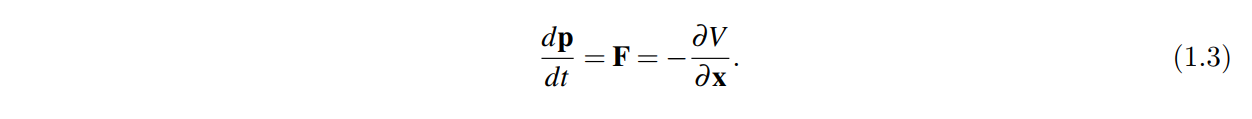
左边的等式是牛顿运动定律。
对于动量的定义：粒子的速度与动量成正比与质量成反比

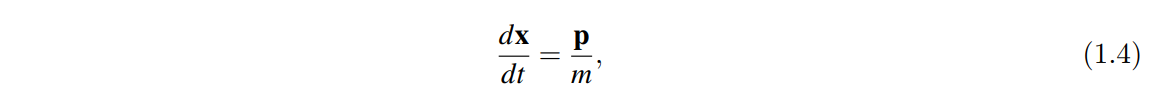
哈密顿正则方程的推导

由哈密顿正则方程我们可以证明能量守恒：（虽然能量守恒应该才是基本前提）

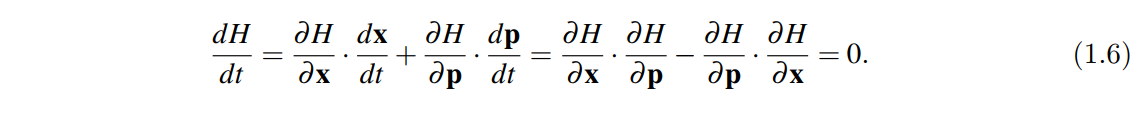
多系统推广此处略。

无磨损摩擦的一个物理模型

微分形式

微分形式

首先是给出坐标变换后二重积分的计算方法

这里说明一下雅可比矩阵：

• 这里的雅可比行列式可以看成两个二维向量叉乘的绝对值，数值上等于两个向量表示的平行四边形的面积
• 两个向量分别是原坐标单位向量变换后，在新坐标中的样子。如下图所示，紫色的两个点代表变换后的单位坐标。
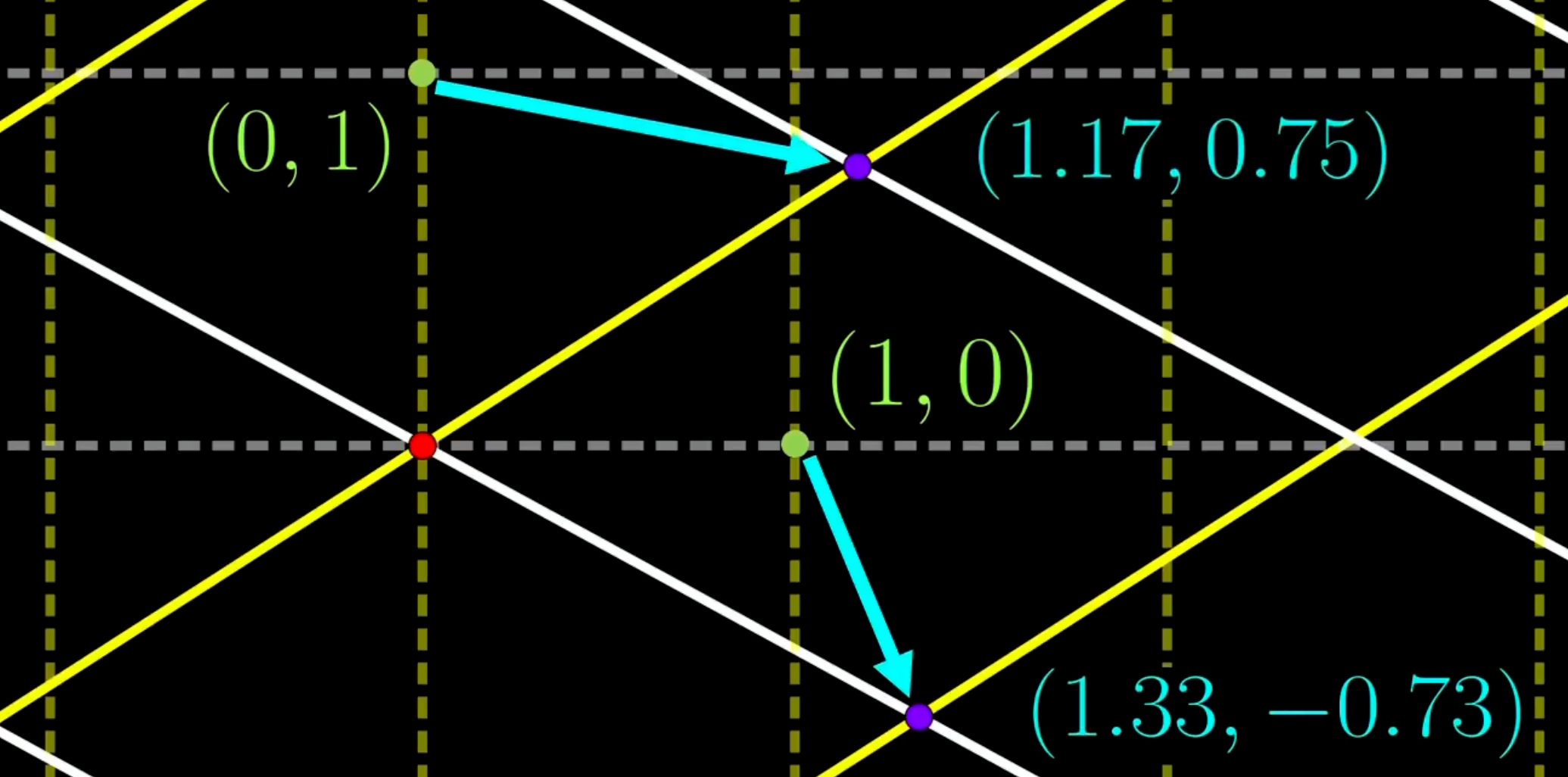
• 雅可比行列式为什么等于叉乘，可以线验证左边原点附近任意夹角的两个单位向量，而其他情况通过平移变成这种情况后，面积不变，由此可以证得。
• 而原单位坐标的面积为1，又有雅可比行列式计算出变换后的面积，因此雅可比矩阵可以表示变换后的面积比。

将以上结果推广到n重积分
我们给出一个这样的标记：


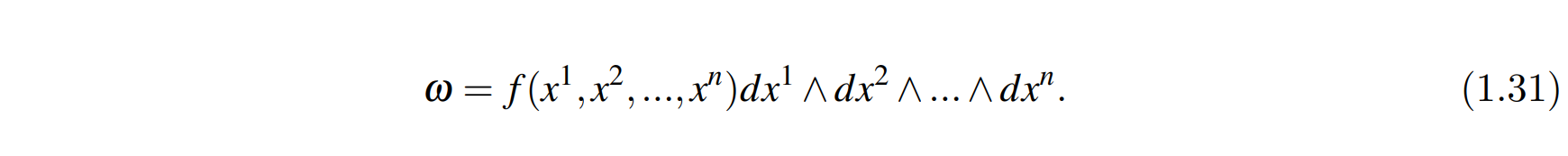
有了上面的n重形式，我们探讨对n个变量（维度）做k重积分的情况（比如在三维空间中做二重积分）

• 注意，k这里可以看成一个张量的维度，2时为一个矩阵，3时为矩阵的叠加。
• 这里是一个爱因斯坦求和约定，当标号同时存在上标和下标中则默认对齐求和，所以这里是省略了前面的k个连加符号（从1加到n）

这样则必然出现：

• k个指标取值必然要两两不同，否则为0。
• k要小于等于n
• 以2-形式继续考察，发现对微分有贡献的项只有反对称的项。

由上式得，当两个指标对称，则对微分无贡献。又由于任意实数可以这样分解：

则对微分有用的必然时反对称的部分（张量总任意两个维度对换，如ij）
而k个微分有k!种排列方式（在反对称的情况下是相等的)，因此要除以k!。

三维的微分形式

三维空间的0-形式和三维空间的1-形式十分类似

接下来写1-形式和2-形式：
将1-形式的写法进行简化

同样对2-形式的写法进行简化

我们由两个简化的式子得到，1-形式和2-形式拥有对应的结构，这种现象称之为霍奇对偶

外微分与斯托克斯公式

散度与旋度

散度

衡量向量场在某一点的局部性质（是源还是汇）

• 源：流出比流入多，散度为正
• 汇：流入比流出多，散度为负

数学定义

从定义可以看出，散度是有默认的正方向的。

旋度

旋度是衡量向量场中某一点的旋转特性。这是一个矢量，其更加右手定则确定旋转方向。旋度的膜长用于衡量旋转的剧烈程度

数学定义：

外微分

我们定义一种运算，以二维空间举例


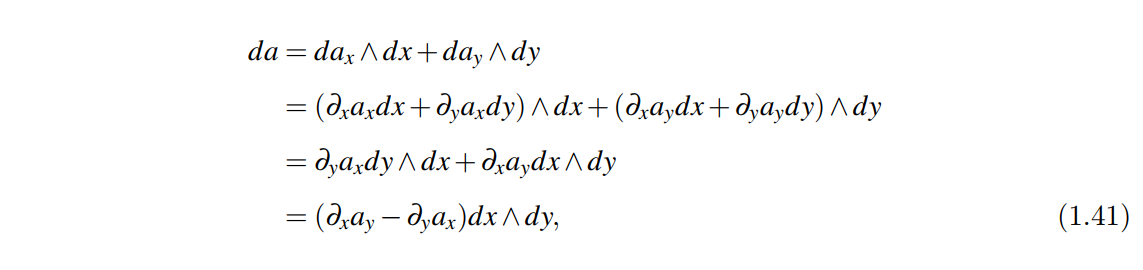
上述式子外积前的内容就是矢量$\mathbf{a}$的散度。
然后我们用外积分重写格林公式


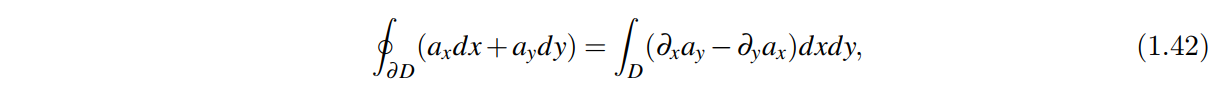
然后我们来写三维空间1-形式微分的外积分

可以看到外积分自动给出了三维空间的旋度
我们再利用这个外积分重写斯托克斯公式

继续推广外积分到三维空间的2-形式微分

我用这个公式重写高斯公式

由上述综合，我们得到了广义的斯托克斯公式

公式两边面的维数和微分的形式k是相等的

这里等于0是因为先对i求导再对j求导和先对j求导再对i求导是相等的（即没有相反的分量）

保守力的特性

我们将保守力换两种形式改写

由新学到的外微分有：

再通过外微分的形式将这个方程拆解开

特别的我们将1，2，3带入（也就是将一个粒子带入）得到保守力旋度为0

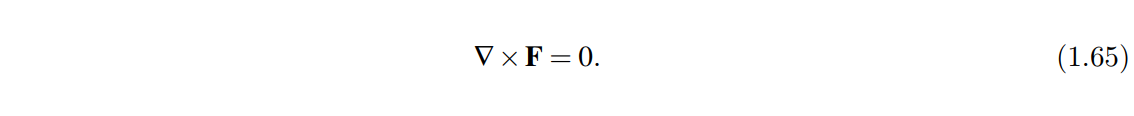
接下来我们探索保守力沿着闭合回路做功

注意这里的F是一个微分形式而不是力本身。这样写是为了符合斯托克斯公式的定义。
由于摩擦力沿闭合回路会将机械能转化为热能，做了负功，因此摩擦力不是保守力。