关于强化学习的一篇经典学习文章
基本概念:
Actor:策略函数,目标是最大化轨迹的期望累积奖励
Critic:价值函数,

Policy Gradient策略梯度:
(介绍逻辑)先让智能体用当前 “玩法” 和环境互动,记录每一步的 “状态、动作、得分”;再分析这些 “经验” 中哪些动作能带来高回报,朝着 “更可能选高回报动作” 的方向调整玩法;不断迭代,直到玩法足够好。
总结路线,初始化参数→与环境交互采样→计算奖励回报→估计策略梯度→更新参数→循环优化
环境:
负面奖励:
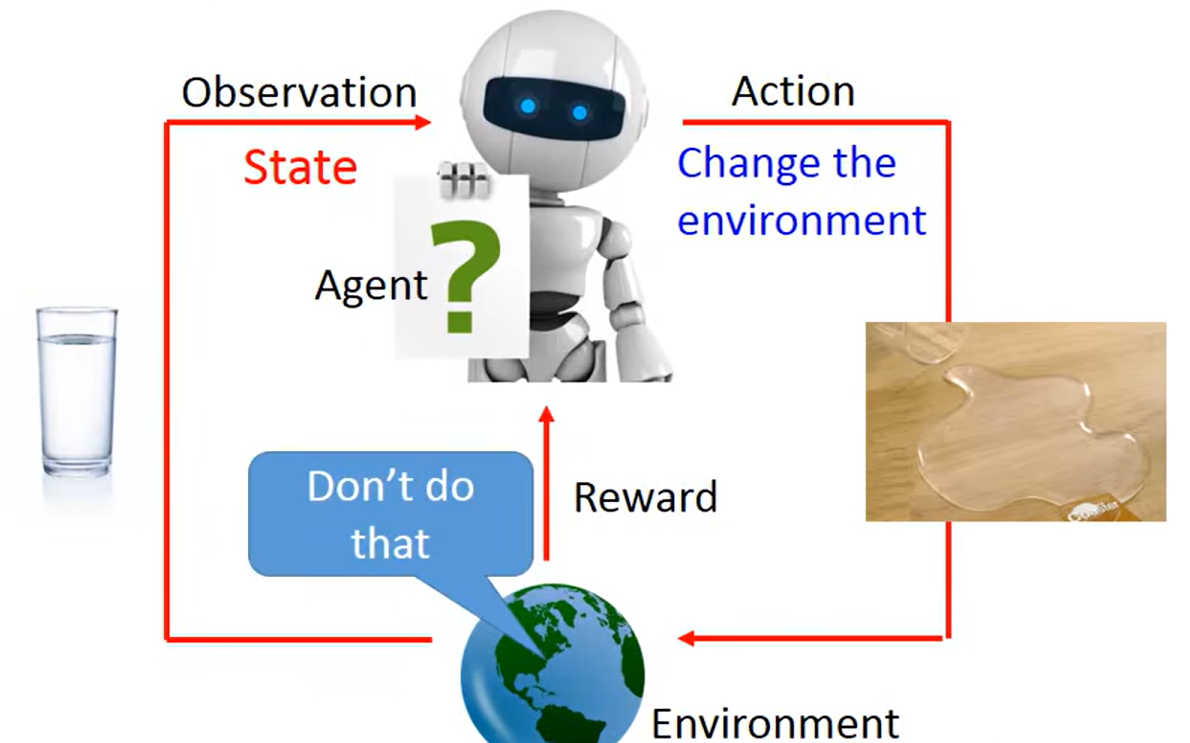
正面奖励:
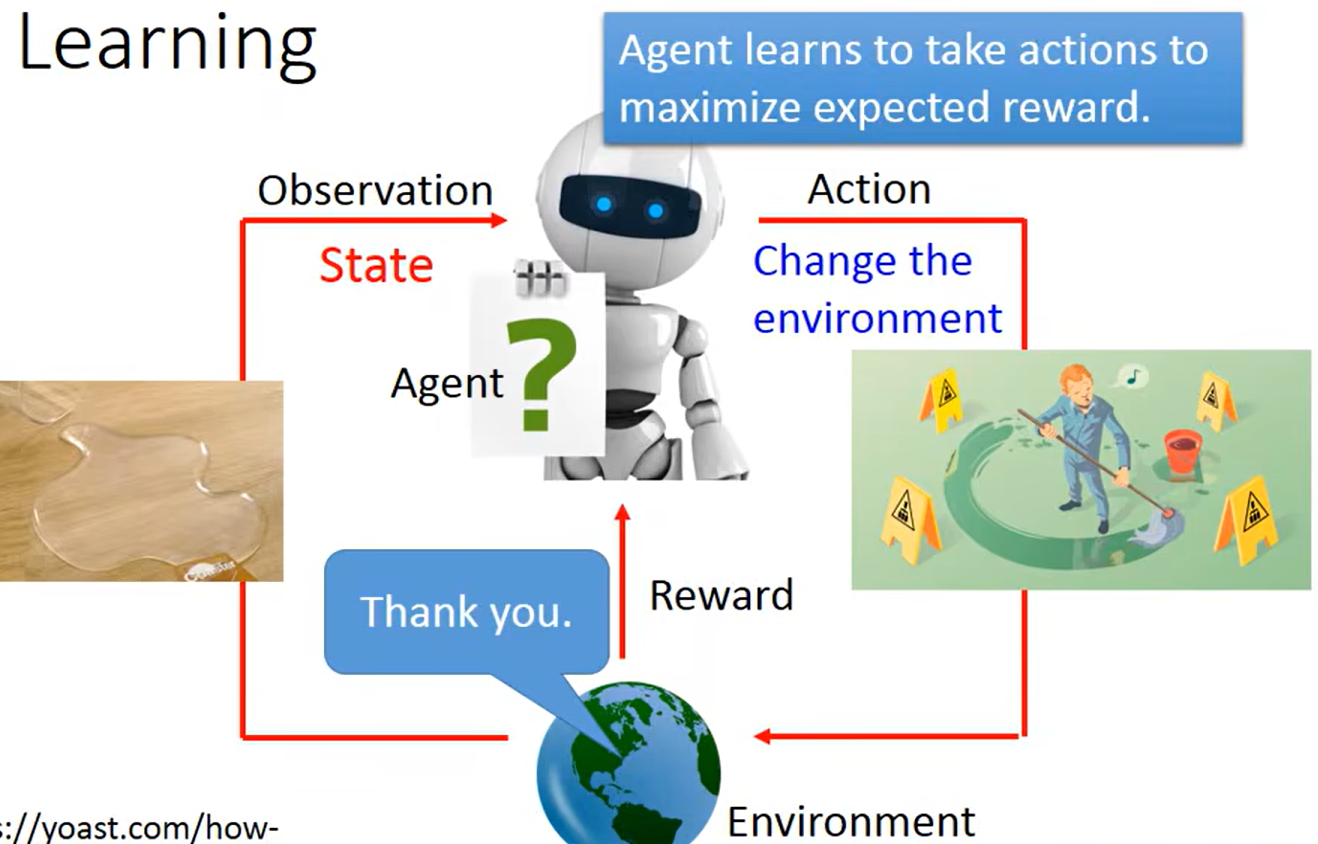
以下是通过对话机器人的训练相关的奖励机制机制来控制结果

Outline(学习方法)
采取中间交叉的Actor+Critic:
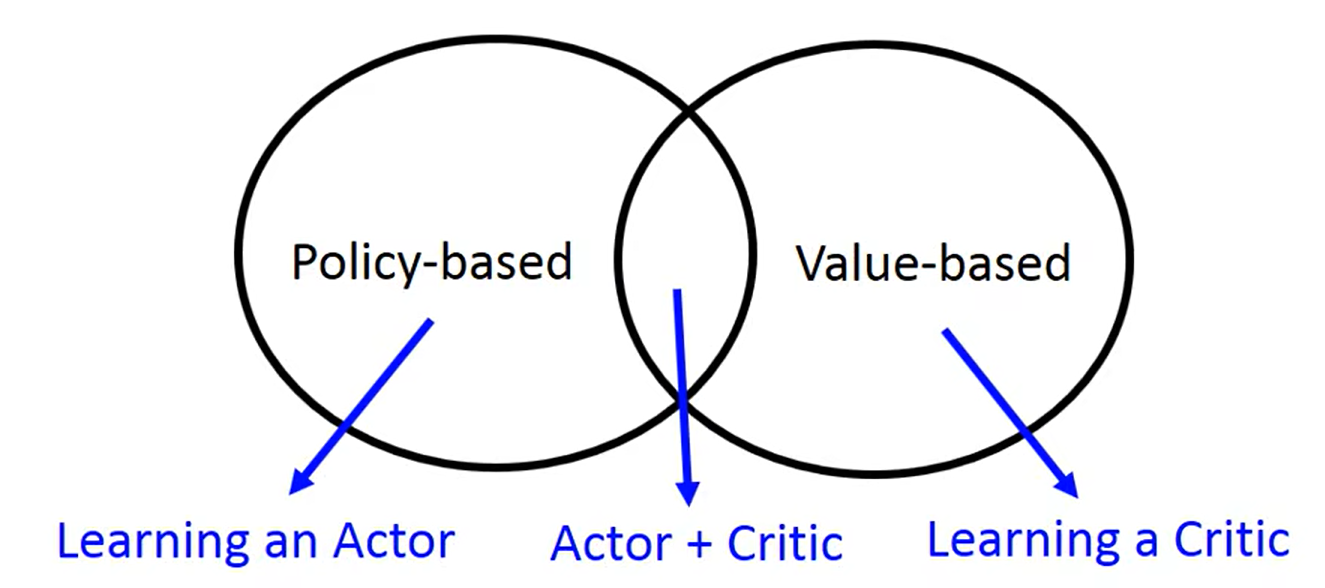
Policy-based Approach——Learing an Actor(学习一个演员)
先是寻找相关的函数,然后进行观察学习,再采取行动
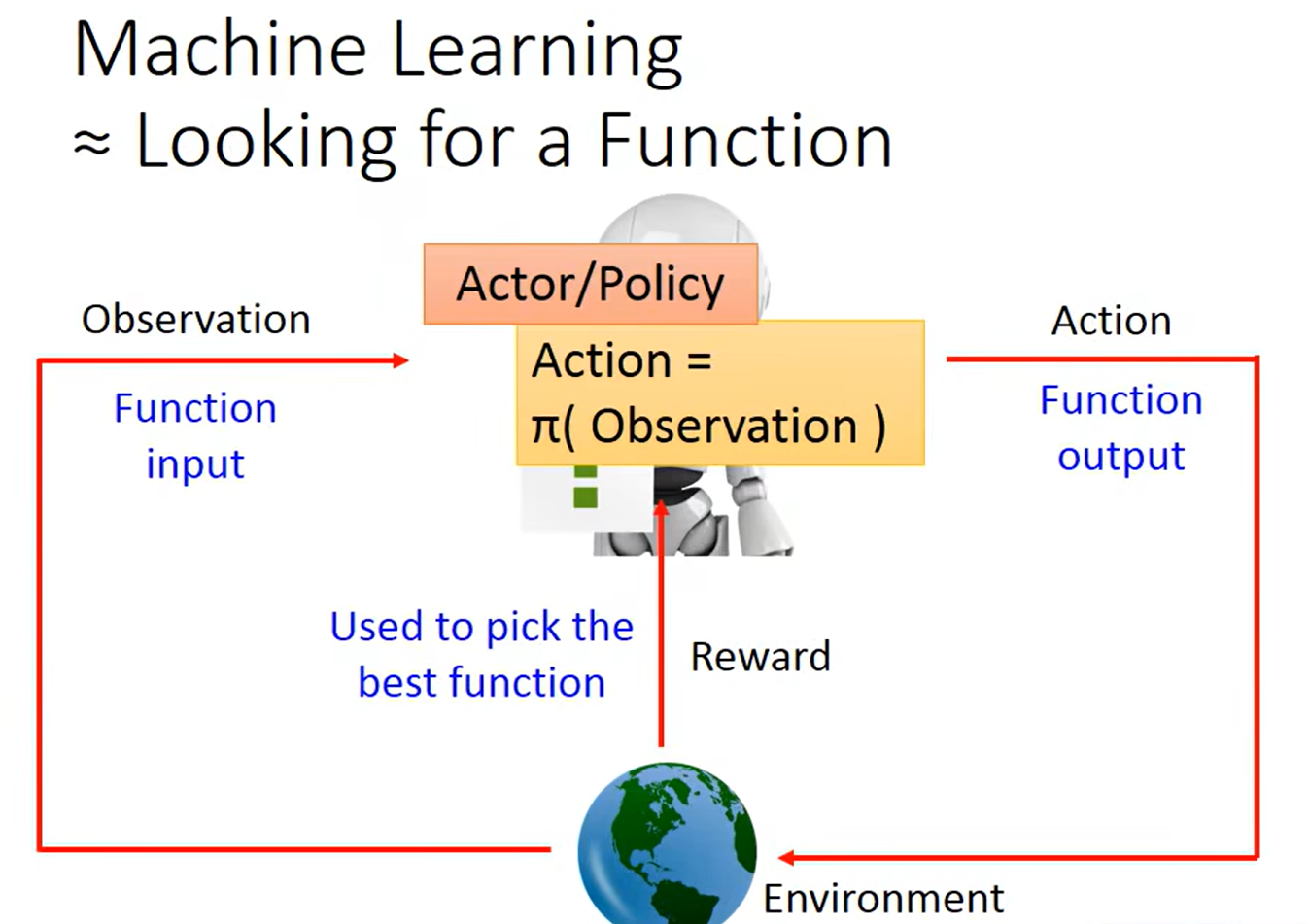
深度学习的三大步:
Step 1:神经网络作为演员
输入层:“观察”环境的动作,查看动作是在做什么
然后到隐藏层中提取观察的特征,转换和计算,学习“从观察到动作之间”的特征关系
输出层:每个神经元可能对应一个动作,输出采取的可能性最大的动作
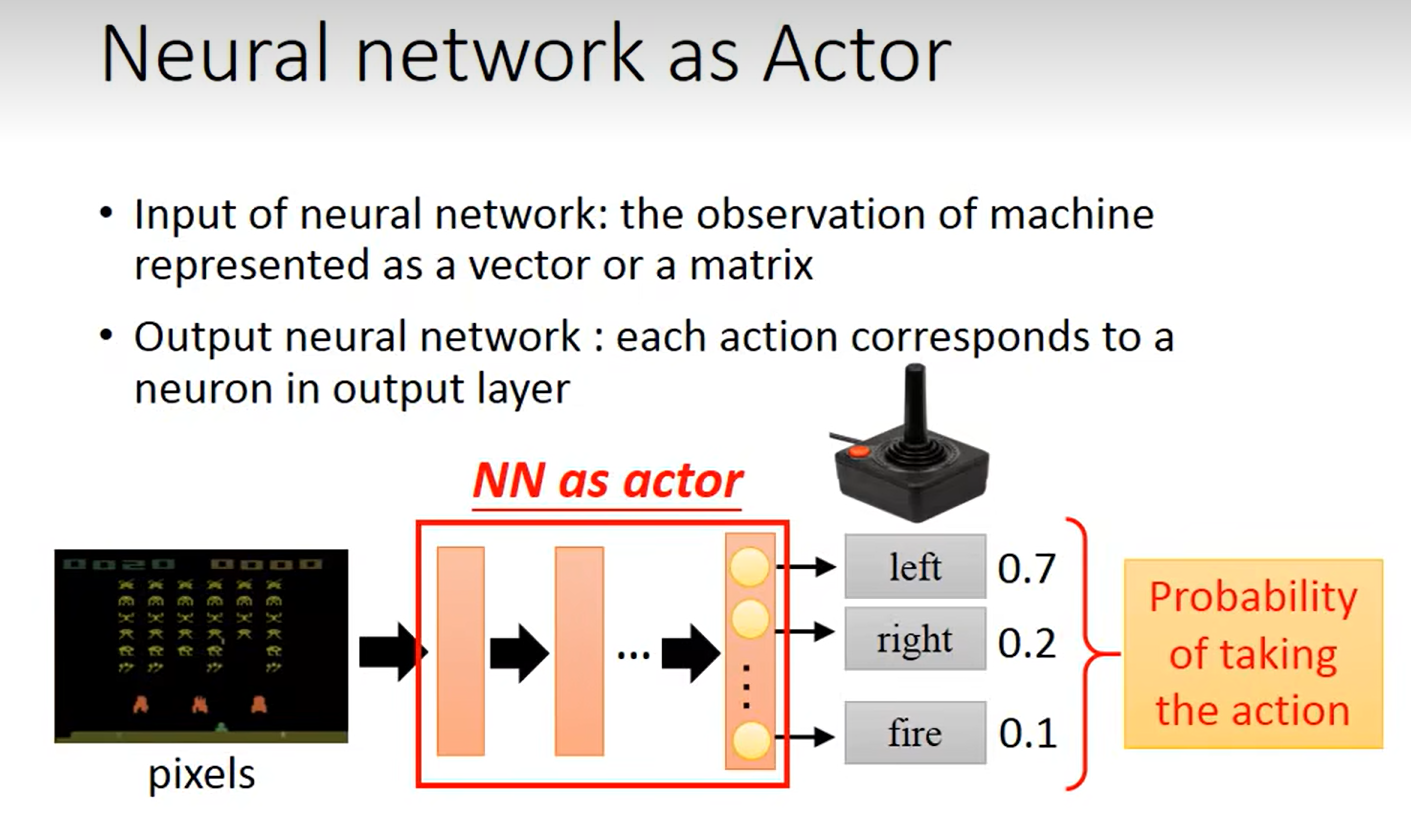
那么思考一个问题,为什么要采用神经网络呢?
因为你可以想想,如果采取了其他固定的奖励机制(如table),比如我达到自己主观设定的阈值就一定选择去执行planA,局限性太大了,这些对于小场景可能适用且效果还不错,但是大场景呢?环境一直在变换,万一遇到之前没设想到的环境,那就不实用了
所以采取神经网络的优点就很明显了,分为以下几点:
1,压缩高维状态(比如游戏去“观察”行为,但是这个观察是连续且高维的,采用table会造成内存爆炸)
2,遇到没见过的状态,神经网络能举一反三,不会被限制
3,端到端的学习(无需人工去提取特征,比如传统的强化学习设计需要人工去表示状态,再表示决策,麻烦且容易出错,采用神经网络则不用,实现“观察”到“动作”的输入到输出)
Step 2:良好的功能性
判断Actor的好坏:
Actor 的本质是一个策略(比如 “左移概率 0.7、右移 0.2、开火 0.1” 的动作概率分布)。判断它 “好坏” 的核心标准是:用这个策略与环境交互时,长期累积奖励的数学期望(平均值)有多高。
计算总损失
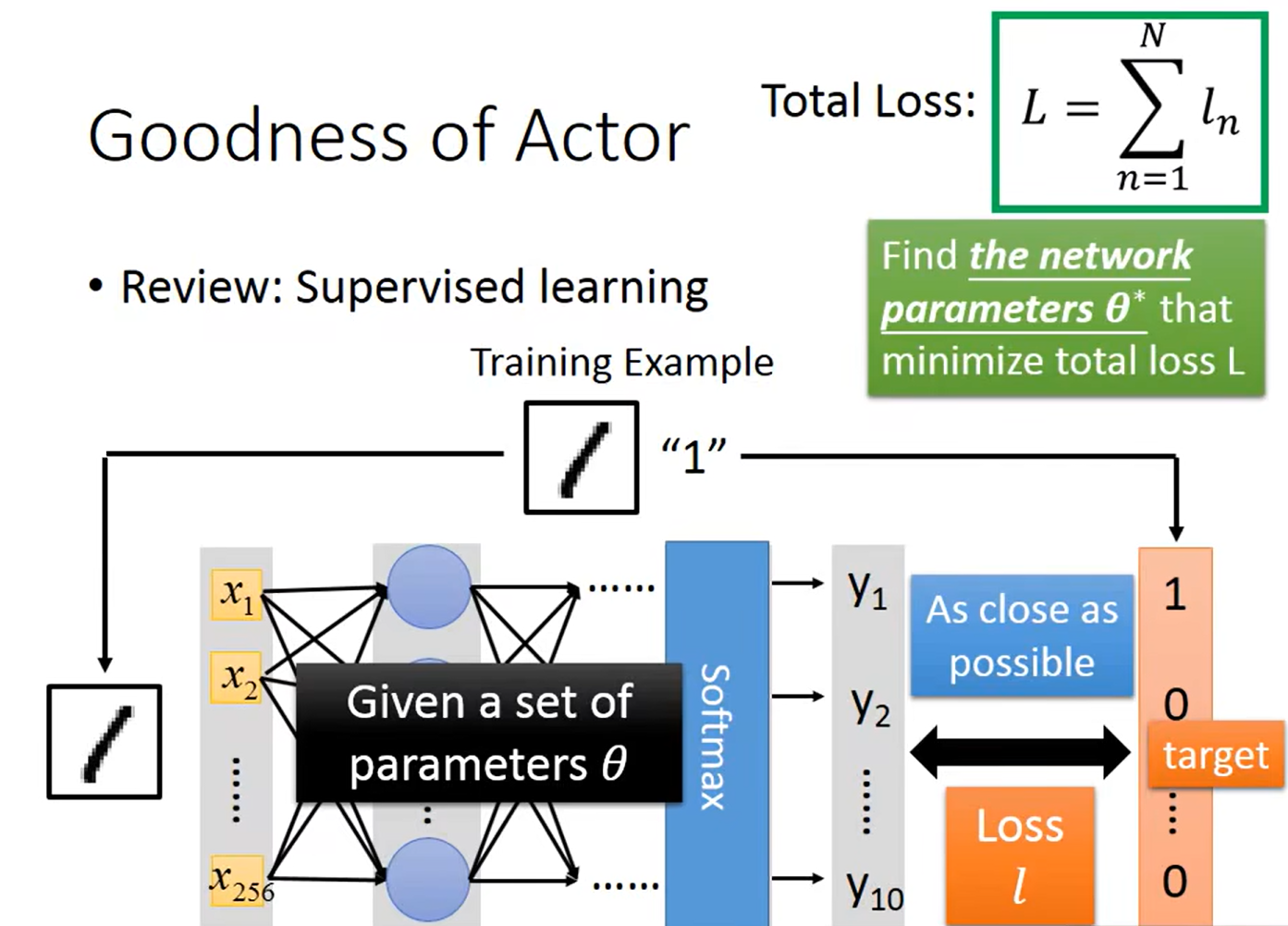
主要是由期望值来决定好坏:
1,简单场景:
在简单的场景下,我们只需要让Actor多测试几把,采平均分
2,复杂场景:
我们需要借助Critic来作辅助,用 Critic 估算 “每个动作的长期价值”,Actor 根据这个来调整策略,最终让 “平均分” 越来越高。
Step 3:衡量选出最好的function
采用添加基线(Baseline)来更加有效地“找到最好的策略函数”,我们从策略梯度和基线的作用来分析:
1,策略梯度的核心目标:最大化“期望累积奖励”:
通过公式来计算出最大化的累积奖励:Rˉθ=Eτ∼pθ(τ)[R(τ)]
为了最大化 Rˉθ,需要计算它的梯度 ∇Rˉθ,并沿梯度方向更新策略参数 θ
注:
Rˉθ=Eτ∼pθ(τ)[R(τ)] ,指的是每次的总奖励之和除以次数,相当于平均值
2,但是对于以上公式去计算累积奖励的话,会出现:奖励“无区分度”导致分差大:
因为会出现一种情况就是,R(τn) 总是正的,会导致一个问题:
所有的动作的概率梯度都会被正奖励放大,会出现即使某些动作不如“平均水平”但是也被错误地“鼓励(概率提高)”
这种问题出现就会导致梯度估计的方差极大(Actor更新方向错乱),导致策略效率低下
3,基线(Baseline)的作用:“中心化”奖励,精准区分动作好坏:
为了解决以上问题,我们引入了Baseline,将梯度纠正为:
∇Rˉθ≈N1∑n=1N∑t=1Tn(R(τn)−b)∇logp(atn∣stn,θ)
用Baseline来区分 “好动作” 和 “一般动作”:
- 若 R(τn)>b(当前轨迹奖励 “高于基准”),则 (R(τn)−b)>0,会鼓励该轨迹中动作(提高动作概率);
- 若 R(τn)<b(当前轨迹奖励 “低于基准”),则 (R(τn)−b)<0,会抑制该轨迹中动作(降低动作概率)。
即使整体奖励都为正,也能通过 “与基线的比较”,精准区分动作的实际价值
总的来说:基线不改变梯度的 “期望方向”,但能大幅降低梯度的方差,让参数更新更稳定、高效。
做到:
- 方差降低 → 每次更新的方向更可靠,不会因随机波动偏离最优路径;
- 奖励区分度提升 → 能更准确地 “强化好动作,削弱差动作”。
Policy Gradient(策略梯度)
不断收集新的数据,进行带入优化,不断更新参数
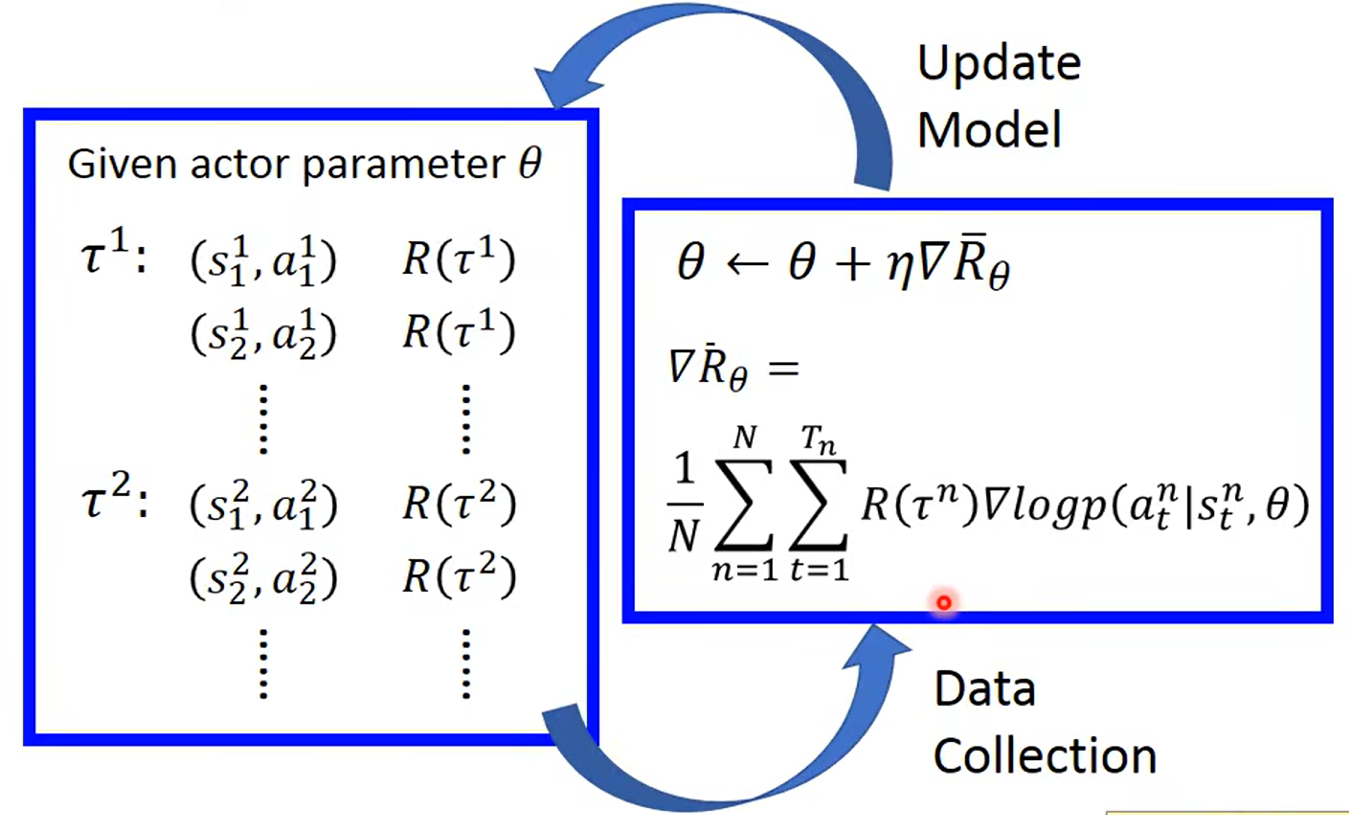
几种变法与相关的使用场景:
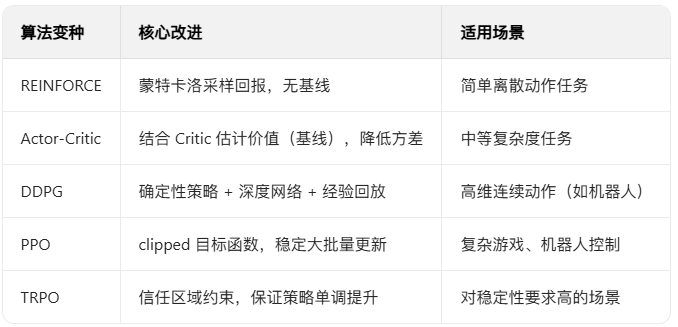
(前面我们学习的都是Actor-Critic,接下来看其他文章去学习一下其他的方法)
