当前位置：首页 > news >正文

多对多依赖；有向无环图l；拓扑排序；DFS回溯输出全路径简述

news 2025/9/20 6:47:35

概述

在业务中经常会一到一些场景数据之间有依赖关系；简单的依赖可以用树结构处理，但是一些复杂的依赖树结构就满足不了了（比如任务A需要依赖任务B和C，此时相当于有2个父节点，树结构满足不了）

此时可以用有向无环图（DAG）来实现；
通过DFS回溯（深度优先遍历）可以输出所有路径（依赖关系图）

拓扑排序

表结构的话也比较简单,单向依赖就行；
大致逻辑是
1-先统计单级依赖关系 + 每个任务的入度
2-再用队列维护入度=0的任务
3-最后遍历得出所有任务的执行路径

//任务表
CREATE TABLE task (id BIGINT PRIMARY KEY,name VARCHAR(255),status VARCHAR(50),
);//依赖表
CREATE TABLE task_dependency (task_id BIGINT NOT NULL,        -- 子任务 (A)dependency_id BIGINT NOT NULL,  -- 前置依赖任务 (B)PRIMARY KEY (task_id, dependency_id)
);

public static class Dependency {String taskId;String dependencyId;public Dependency(String taskId, String dependencyId) {this.taskId = taskId;this.dependencyId = dependencyId;}
}public static void main(String[] args) {List<String> tasks = Arrays.asList("A", "B", "C", "D");List<Dependency> deps = Arrays.asList(new Dependency("A", "B"), // A 依赖 Bnew Dependency("A", "C"), // A 依赖 Cnew Dependency("D", "A")  // D 依赖 A);//统计任务的入度Map<String, Integer> inDegreeMap = new HashMap<>();//任务和依赖当前任务的集合Map<String, List<String>> graphMap = new HashMap<>();for (String task : tasks) {inDegreeMap.put(task, 0);graphMap.put(task, new ArrayList<>());}for (Dependency dep : deps) {//任务依赖关系;(前置任务下有多少子任务)graphMap.computeIfPresent(dep.dependencyId,(k, old)-> {old.add(dep.taskId);return old;});// 统计任务的入度// 这里的入度统计是和逻辑反着的// 比如A->B，在逻辑上是A依赖B;但是在DGA里是标识为 B -> A，表明B是A的前置条件，只有B完成了才能开始A；// 所以此时这里统计的入度是taskId ++inDegreeMap.computeIfPresent(dep.taskId,(k, oldValue)-> ++oldValue);}Queue<String> rootQueue = inDegreeMap.entrySet().stream()//捞出入度为0的，即为起点.filter(it -> Objects.equals(0, it.getValue())).map(Map.Entry::getKey).distinct().collect(Collectors.toCollection(LinkedList::new));//拓扑图输出；即从根点到终点的结果序列，只能保证根点一定在终点前，中间的元素顺序不一定是固定的List<String> resultPath = new ArrayList<>();while (!rootQueue.isEmpty()){//入度为0的根节点String rootNode = rootQueue.poll();resultPath.add(rootNode);for (String next : graphMap.get(rootNode)) {//当前前置任务下的依赖子任务//当前子任务的入度-1inDegreeMap.computeIfPresent(next, (k, oldValue) -> --oldValue);//如果当前子任务的入度为0，则加到根节点队列末尾，即在遍历中其可以作为一个起点出发了if (inDegreeMap.get(next) == 0) rootQueue.offer(next);}}if (resultPath.size() != tasks.size()) {//有环路时，拓扑排序总路径数量!=总路径数量；因为有循环的话根节点队列无法offer所有节点throw new RuntimeException("检测到循环依赖，无法进行拓扑排序！");}System.out.println(resultPath);
}

DFS回溯输出所有路径

和上面的拓扑排序不一样，这儿是明确输出了所有路径
通过DFS回溯遍历方式

以如下关系路径做为demo
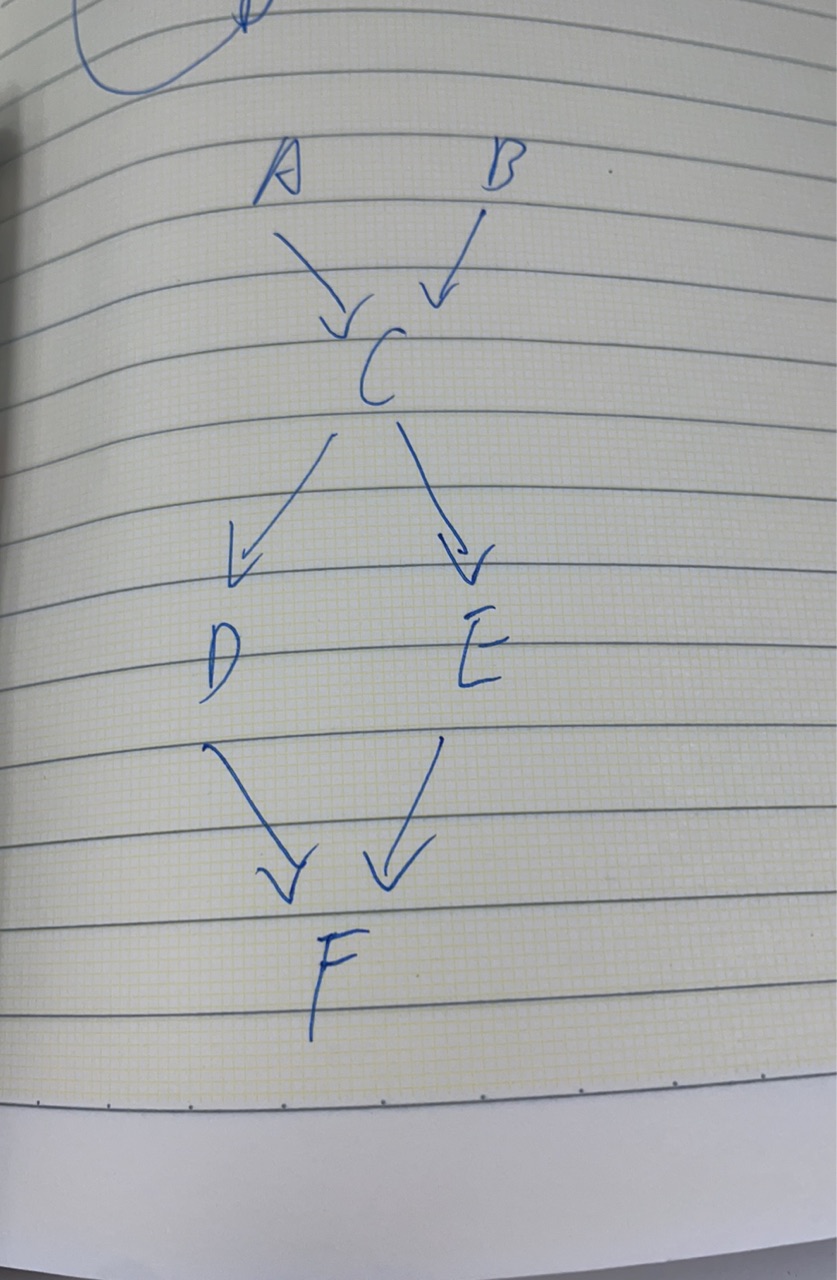
在这里插入图片描述

public static void main(String[] args) {// 单向关系图Map<String, List<String>> graph = new HashMap<>();//A是C的前置任务graph.put("A", Arrays.asList("C"));//B是C的前置任务graph.put("B", Arrays.asList("C"));//C是D、E的前置任务graph.put("C", Arrays.asList("D", "E"));//B是F的前置任务graph.put("D", Arrays.asList("F"));//E是F的前置任务graph.put("E", Arrays.asList("F"));// F是终点graph.put("F", Collections.emptyList());// 计算入度Map<String, Integer> inDegree = new HashMap<>();for (String node : graph.keySet()) {inDegree.putIfAbsent(node, 0);for (String nei : graph.get(node)) {inDegree.put(nei, inDegree.getOrDefault(nei, 0) + 1);}}// 找出起点（入度为 0）List<String> startList = inDegree.entrySet().stream()// 入度为0的就是起点.filter(it -> it.getValue() == 0).map(Map.Entry::getKey).collect(Collectors.toList());// 找出终点（出度为 0）List<String> endList = graph.entrySet().stream()//下面没有挂子节点的就是终点.filter(it -> CollectionUtil.isEmpty(it.getValue())).map(Map.Entry::getKey).collect(Collectors.toList());// 遍历所有起点到终点的路径List<List<String>> allPaths = new ArrayList<>();for (String start : startList) {dfs(graph, start, endList, new ArrayList<>(), allPaths);}// 输出结果System.out.println("所有起点到终点的路径:");for (List<String> path : allPaths) {System.out.println(path);}}private static void dfs(Map<String, List<String>> graph,String current,List<String> ends,List<String> path,List<List<String>> allPaths) {//添加当前节点path.add(current);if (ends.contains(current)) {//到达终点时保存一份路径allPaths.add(new ArrayList<>(path));} else {for (String nei : graph.getOrDefault(current, Collections.emptyList())) {//将当前节点的子节点作为起点，继续递归遍历dfs(graph, nei, ends, path, allPaths);}}//回溯,回到上一个节点path.remove(path.size() - 1);
}