当前位置：首页 > news >正文

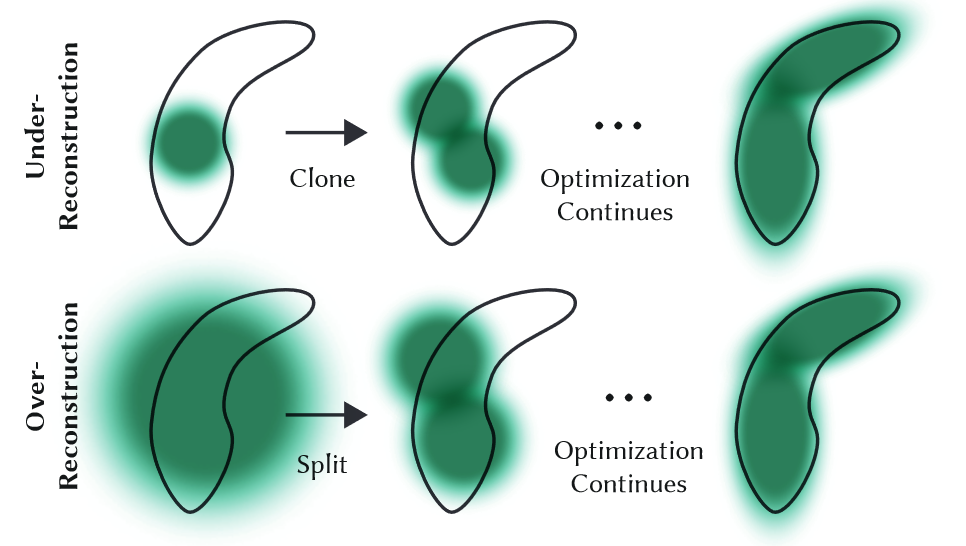
基于 3D 高斯泼溅的重建 (3DGS-based)

news 2025/9/19 14:25:31

3DGS (3D Gaussian Splatting) 是比 NeRF 更晚出现的技术，它在保持高质量渲染的同时，极大地缩短了训练时间并实现了实时渲染。

核心思想：与 NeRF 使用隐式的神经网络不同，3DGS 用一组离散的、可优化的 3D 高斯函数来显式地表示场景。每个高斯函数都有位置、形状（各向异性协方差）、颜色和不透明度，球谐函数（SH）系数等属性。渲染时，这些 3D 高斯函数被“泼溅”(Splatting) 到 2D 图像平面上，并通过 alpha-blending 混合成最终的图像

(1)

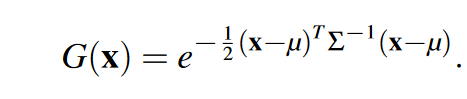
这个公式的用途是什么？ 它的作用是定义场景中的一个基本元素——一个“三维高斯体”。你可以把它想象成一个在三维空间中的、半透明的、有形状的“能量团”或“棉花糖”。整个三维场景就是由成千上万个这样的“高斯体”组合而成的。这个公式告诉我们，在空间中的任意点 x，它受这个高斯体的影响有多大（或者说密度有多高）。

公式拆解：

G(x)：这是函数的输出。它表示在三维空间中的点 x 处，这个高斯体的“密度”或者“强度”值。这个值是一个标量（一个数字）。
x：代表三维空间中的任意一个点，是一个三维向量 (x, y, z)。
μ (mu)：这是这个高斯体的中心点（mean），也是一个三维向量 (μx, μy, μz)。这个点是高斯体密度最高的地方。
Σ (Sigma)：这是一个 3x3 的协方差矩阵 (covariance matrix)。这是最关键的部分，它描述了这个高斯体的 形状、大小和朝向。
- 如果 Σ 是一个对角矩阵（只有对角线上有值），那么这个高斯体就是一个轴对齐的椭球体，对角线上的值分别控制它在 x, y, z 三个轴上的“胖瘦”（即缩放）。
- 如果 Σ 是一个更复杂的矩阵，比如除了对角线，在矩阵其他位置也有值，它还能描述这个椭球体的旋转。所以，通过 Σ，这个“棉花糖”可以被任意地拉伸、压缩和旋转。

$\Sigma^{−1}$ \Sigma^{−1}：Σ 的逆矩阵。
(x−μ)：这是一个从高斯中心 μ 指向点 x 的向量。它描述了点 x 相对于高斯中心的距离和方向。
(x−μ)^TΣ^{−1}(x−μ)：这部分在数学上被称为“马氏距离的平方 (squared Mahalanobis distance)”。你可以把它理解为一种“考虑了高斯体形状的距离”。如果一个点沿着椭球体“长轴”方向偏离中心，即使物理距离很远，这个值也可能不大；但如果它沿着“短轴”方向偏离中心，即使物理距离很近，这个值也可能很大。
e−...：指数函数。它的特性是，当括号里的值为 0 时（即 x=μ，在中心点），函数值为 e0=1 (最大值)；当 x 离中心点 μ 越远，括号里的值越大，整个函数值就以指数形式快速衰减并趋近于 0。

(2) Rendering

为了将由3D高斯函数组成的场景渲染到2D图像空间中，3DGS采用了 splatting 光栅化技术。

a) 3DGS设计了一种基于tile的光栅化器。屏幕首先被划分为tile（例如，16×16像素），每个高斯会根据它们重叠的tile数量进行实例化，并被分配一个记录视图空间深度和tile ID的键。然后，高斯会根据其深度进行排序，这使得光栅化器能够正确处理遮挡和重叠的几何图形。

单个采样点的不透明度计算:

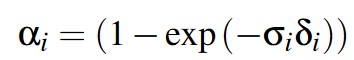
这个公式的用途是什么？当我们要渲染一个像素时，我们会从相机（眼睛）发射一条光线穿过场景。这条光线会穿过很多高斯体。这个公式计算的是，当光线前进一小步（一个间隔 δi）时，在那个点上由高斯体产生的不透明度 (alpha, α)。不透明度的值在 0 到 1 之间，0 代表完全透明，1 代表完全不透明。

αi：第 i 个采样点的不透明度。
σi (sigma)：这是第 i 个采样点的 密度 (density)。这个密度值是从高斯体在那个点的属性中计算出来的。σ 越大，说明那个地方的“物质”越密集，光线越难穿过。
δi：这是光线上传播的微小距离间隔 (interval)。可以理解为从上一个采样点到当前采样点的距离。
σiδi：密度乘以距离。在体积渲染中，这代表了光线在这段微小距离中衰减的程度，可以理解为“光学厚度 (optical thickness)”。
exp(−σiδi)：这计算的是 透过率 (transmittance)，即有多少比例的光能够成功穿过这一小段距离而不被吸收或散射。
1−exp(...)：既然 exp(...) 是穿过去的比例，那么用 1 减去它，剩下的就是 被阻挡的比例，这正是“不透明度”的定义。

最终像素颜色的混合渲染:

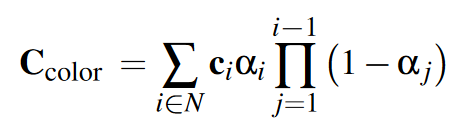
这个公式的用途是什么？ 这是最终的渲染公式。它将光线上所有采样点（i∈N）的颜色和不透明度进行 从前到后 的混合，最终计算出这个像素应该显示的颜色。

C_{color}：这是最终计算出的像素颜色，是一个 RGB 向量。
∑_{i∈N}表示对光线路径上所有采样点（从最靠近相机的 i=1 开始，一直到最远的 N）的贡献进行求和。
ci：第 i 个采样点的颜色，是一个 RGB 向量。这个颜色也是从高斯体的属性中获取的。
αi：第 i 个采样点的不透明度，由我们刚刚分析的公式计算得出。
ciαi：将第 i 个点的颜色乘以它的不透明度。这代表了这个点本身能贡献出的颜色量。一个很亮但很透明的点，贡献的颜色也很少。
∏_{j=1}^{i−1}(1−α_j)：这是最核心的累积透过率 (accumulated transmittance) 部分。
∏ 是连乘符号。
(1−αj)：这是第 j 个点（在当前点 i 前面的某个点）的透过率。如果 αj 是不透明度，那么 1−αj 就是光能通过的比例。
∏_{j=1}^{i−1}(1−α_j)：它将从相机开始，到当前点 i之前的所有点 (j=1 到 i−1) 的透过率全部乘起来。这个结果代表了有多少光能够毫发无损地穿过前面所有的遮挡物，最终到达第 i 个点。

将所有部分组合起来理解：对于光线上的第 i 个点，它的颜色贡献是：该点的颜色(c_i) × 该点的不透明度(α_i) × 光线能到达该点的比例(累积透过率)

最后，∑ 符号将所有点（从前到后）的颜色贡献全部累加起来，就得到了这个像素的最终颜色。前面的点因为累积透过率高（路径上遮挡少），对最终颜色的贡献权重更大；后面的点因为光线被前面消耗了很多，所以贡献的权重就更小。这完美地模拟了物体之间互相遮挡的效果。

(3) Optimization

在前一步“渲染 (Rendering)”中，我们使用一组固定的高斯体参数（位置、形状、颜色、不透明度）来生成一张图像。而“优化”这一步的目的，就是要 找到最优的那组参数，使得渲染出来的图像和真实的训练照片（Ground Truth）尽可能地一模一样。这通过随机梯度下降去更新高斯的可学习参数（位置 μ、形状/协方差Σ、颜色/SH 系数、密度等）。

两件初始化/训练上的事

协方差初始化：一开始把每个高斯设成各向同性\Sigma=s^2 I，其中 s取“到最近 3 个点的平均距离”。这样半径与点云局部密度匹配，不会太小漏掉，也不会太大糊一片。
学习率调度：对位置参数使用“指数衰减”的学习率（类似 Plenoxels 的做法）。直觉：前期步子大，快速把高斯移到合适位置；后期步子小，微调避免抖动。其他参数可以用更平稳或常数学习率。

混合损失函数 (Combined Loss Function)

这个公式的用途是什么？ 这是一个总的损失函数，它将两种不同的“差异”评估方法——L1 和 LD-SSIM——聪明地结合在了一起。它不是只用一种标准来评判“像不像”，而是综合了两种标准的优点。

公式拆解：

L：最终的总损失值。我们的优化目标就是让这个 L 越小越好。
L1：即 L1 损失，它主要关注 像素级别的绝对颜色差异。
LD-SSIM：即 D-SSIM 损失。它主要关注 图像的结构、纹理和对比度等感知上的相似性，更符合人眼的判断。
λ (lambda)：这是一个超参数（人为设定的一个值，通常在0到1之间），它充当一个 “平衡旋钮”。

- 如果 λ 很大（比如 0.8），就意味着我们更看重 LD-SSIM，希望渲染图在结构上更像真照片。
- 如果 λ 很小（比如 0.2，这是论文中常用的值），就意味着我们更看重 L1，希望渲染图在每个像素的颜色上都精确匹配。

L1 损失 (L1 Loss)

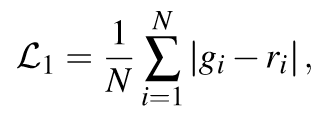
这个公式的用途是什么？它用最直接的方式计算两张图的差异：逐个比较每个像素的颜色，然后将所有差异加起来求平均。

公式拆解：

N：图像中的总像素数量。。
gi：第 i 个像素在 ground truth（真实照片）中的颜色值（通常是一个RGB向量）。
ri：第 i 个像素在 rendered（渲染图像）中的颜色值。
∣gi−ri∣：计算两个像素颜色值的绝对差。例如，如果真实像素是 (255, 0, 0) (红色)，渲染像素是 (250, 10, 0)，绝对差就是 (5, 10, 0)。取绝对值是为了避免正负差异相互抵消。
1/N∑. .：将所有像素的绝对差加起来，再除以总像素数 N，得到平均绝对误差 (Mean Absolute Error, MAE)。

D-SSIM 损失 (Dis Structural Similarity Loss)

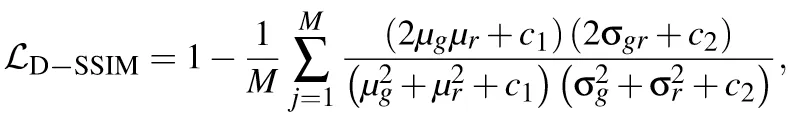
这个公式的用途是什么？这个公式看起来很复杂，但它的核心思想是：模仿人类视觉系统来判断两张图片的相似度。人眼对像素的绝对值差异不敏感，但对亮度、对比度和结构的变化非常敏感。SSIM（结构相似性指数）就是为此设计的。而 LD-SSIM 就是 1 - SSIM，即结构“不”相似度，我们希望这个不相似度最小。

这个计算不是针对单个像素，而是针对图像中的一个个“局部窗口 (local windows)”（比如 8x8 的小方块）进行的。

公式拆解：

首先，后面那个巨大的分数部分，计算的是单个窗口的 SSIM 值。SSIM 值越接近 1，代表两个窗口越相似。
μg 和 μr：分别代表真实图像窗口和渲染图像窗口的像素平均强度（均值）。这部分用于比较两者的亮度 (Luminance)。
σg2 和 σr2 ：分别代表两个窗口的像素方差 (Variance)。方差衡量了数据的离散程度，在这里可以理解为图像的对比度 (Contrast)。
σgr ：代表两个窗口的协方差 (Covariance)。它衡量了两个窗口像素值的线性关系，可以理解为对结构信息 (Structure) 的比较。
c1 和 c2：两个很小的常数。它们的作用是增加分母的稳定性，防止当分母接近于 0 时（例如在一个纯黑色的窗口里，μ 和 σ 都可能为0）出现计算错误。
$\frac{1}{M}∑_{j=1}^M...$ ... ：将图像划分为 M 个窗口，分别计算每个窗口的 SSIM 值，然后求平均，得到整张图的平均 SSIM。
1−...：用 1 减去平均 SSIM 值。这样，如果两张图完全一样（SSIM=1），损失值 LD-SSIM 就为 0，这正是我们想要的优化目标。