矩阵分析线性表示例题

（1）问题求解关于线性变换的矩阵表示

知识点分析

知识点如图所示

（法一）令$P$是从基 {αi}\{\alpha_i\}{αi​} 到标准基的过渡矩阵

线性变换$SS$在基 {α1,α2,α3}\{\alpha_1, \alpha_2, \alpha_3\}{α1​,α2​,α3​} 下的矩阵是$A$。现在要求$SS$在标准基 {e1,e2,e3}\{e_1, e_2, e_3\}{e1​,e2​,e3​} 下的矩阵表示。

设$P$是从标准基到基 {αi}\{\alpha_i\}{αi​} 的变换矩阵($P$是从基 {αi}\{\alpha_i\}{αi​} 到标准基的过渡矩阵)。这意味着$P$是 (α1,α2,α3)−1{e1,e2,e3}(\alpha_1, \alpha_2, \alpha_3)^{-1}\{e_1, e_2, e_3\}(α1​,α2​,α3​)−1{e1​,e2​,e3​}。

所以，如果有一个向量在 {αi}\{\alpha_i\}{αi​} 基下的坐标是 $x$，那么它在标准基下的坐标是 $P^{-1}x$.

线性变换$SS$在{αi}\{\alpha_i\}{αi​}基下的矩阵表示是$A$，所以如果输入向量在{αi}\{\alpha_i\}{αi​}基下的坐标是 $x$，那么输出向量在 {αi}\{\alpha_i\}{αi​}基下的坐标是 $Ax$。

我们需要输出在标准基下的坐标。

由于输出向量在{αi}\{\alpha_i\}{αi​} 基下的坐标是$Ax$，而标准基下的坐标是$P^{-1}(Ax)$.

另一方面，输入向量在标准基下的坐标是$P^{-1}x$。我们想要找到矩阵$B$，使得当输入在标准基下的坐标是$y$时，输出在标准基下的坐标是$By$.

所以，设$y=P^{-1}x$，则$x=Py$。输出在标准基下的坐标是$P^{-1}Ax=P^{-1}A(Py)=(P^{-1}AP)y$.

因此，$B=P^{-1}AP$.

python代码求解

import numpy as np# 定义矩阵 A
A = np.array([[1, 0, -1],[1, 1, 0],[-1, 2, 3]])# 定义基向量
α1 = np.array([-1, 1, 1])
α2 = np.array([1, 0, -1])
α3 = np.array([0, 1, 1])# 构建基向量矩阵
alpha_matrix = np.column_stack((α1, α2, α3))# 标准基矩阵
epsilon_matrix = np.eye(3)# 求过渡矩阵 P(P为从标准基到基α的过渡矩阵)，使得 epsilon = alpha * P
# 即 P = alpha^{-1} * epsilon
P = np.linalg.inv(alpha_matrix) @ epsilon_matrix# 计算标准基下的矩阵表示 B = P^{-1} A P
B = np.linalg.inv(P) @ A @ Pprint("在标准基下的矩阵 B 是：\n",B)

（法二）令$P$是从标准基到基 {αi}\{\alpha_i\}{αi​} 的过渡矩阵

线性变换$SS$在基 {α1,α2,α3}\{\alpha_1, \alpha_2, \alpha_3\}{α1​,α2​,α3​} 下的矩阵是$A$。现在要求$SS$在标准基 {e1,e2,e3}\{e_1, e_2, e_3\}{e1​,e2​,e3​} 下的矩阵表示。

设$P$是从基 {αi}\{\alpha_i\}{αi​} 到标准基的变换矩阵($P$是从标准基到基 {αi}\{\alpha_i\}{αi​} 的过渡矩阵)。这意味着$P$是{e1,e2,e3}−1(α1,α2,α3)\{e_1, e_2, e_3\}^{-1}(\alpha_1, \alpha_2, \alpha_3){e1​,e2​,e3​}−1(α1​,α2​,α3​)，即$P$的列向量是${\alpha }_1,{\alpha }_2,{\alpha }_3$。

所以，如果有一个向量在 {αi}\{\alpha_i\}{αi​} 基下的坐标是 $x$，那么它在标准基下的坐标是 $Px$.

线性变换$SS$在{αi}\{\alpha_i\}{αi​}基下的矩阵表示是$A$，所以如果输入向量在{αi}\{\alpha_i\}{αi​}基下的坐标是 $x$，那么输出向量在 {αi}\{\alpha_i\}{αi​}基下的坐标是 $Ax$。

我们需要输出在标准基下的坐标。

由于输出向量在{αi}\{\alpha_i\}{αi​} 基下的坐标是$Ax$，而标准基下的坐标是$P(Ax)$.

另一方面，输入向量在标准基下的坐标是$Px$。我们想要找到矩阵$B$，使得当输入在标准基下的坐标是$y$时，输出在标准基下的坐标是$By$.

所以，设$y=Px$，则$x=P^{-1}y$。输出在标准基下的坐标是$PAx=PA(P^{-1}y)=(PA{P}^{-1})y$.

因此，$B=PA{P}^{-1}$.

python代码求解

import numpy as np# 定义矩阵 A
A = np.array([[1, 0, -1],[1, 1, 0],[-1, 2, 3]])# 定义基向量,组成过渡矩阵 P(P为从基 α 到标准基的过渡矩阵)
α1 = np.array([-1, 1, 1])
α2 = np.array([1, 0, -1])
α3 = np.array([0, 1, 1])# 把 α1, α2, α3 作为列向量，组成矩阵 P
P = np.column_stack((α1, α2, α3))# 计算 P 的逆矩阵
P_inv = np.linalg.inv(P)# 计算标准基下的矩阵表示 B = P A P^{-1}
B = P @ A @ P_invprint("在标准基下的矩阵 B 是：\n",B)

（2）求线性变换的核与值域

核是齐次方程 Bx=0 的解空间
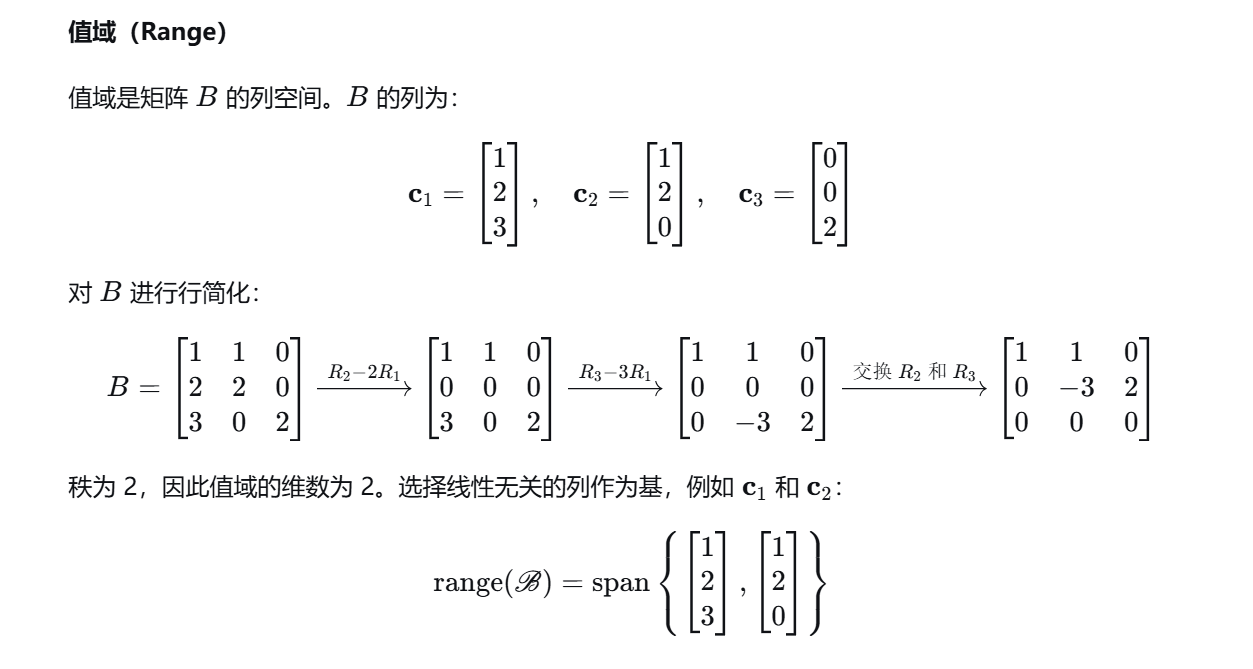
值域是矩阵 B 的列空间

from sympy import Matrix
# 求解核（Kernel）解齐次方程 Bx = 0
B_matrix = Matrix(B)
kernel_basis = B_matrix.nullspace()
print("\n核的基向量:")
for vec in kernel_basis:print(vec)# 求解值域（Range） 值域是矩阵B的列空间
range_basis = B_matrix.columnspace()
print("\n值域的基向量:")
for vec in range_basis:print(vec)