当前位置：首页 > news >正文

算法 --- 优先级队列（堆）

news 2025/9/19 11:35:54

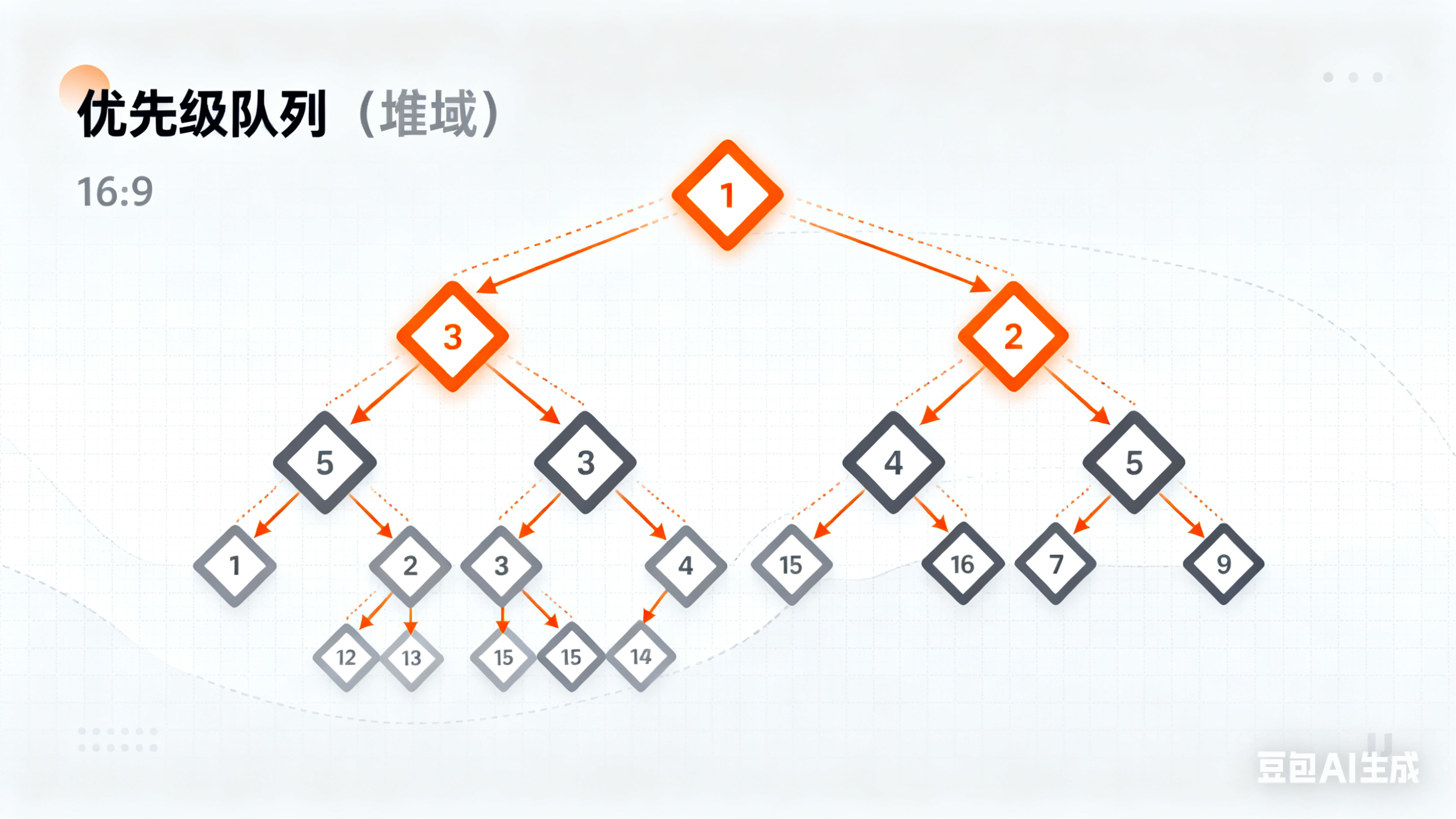
优先级队列（堆）

优先级队列（堆）算法适用于所有需要动态、高效地获取当前一组元素中“最值”（如最大值、最小值、第K大等）的题目。

详细来说，当题目出现以下特征或需求时，就应该考虑使用优先级队列（堆）：

1. 核心场景：动态求极值

这是堆最经典的应用。你有一组数据，数据在不断变化（有新增、有移除），但你需要在任何时刻都能立刻知道当前的最大值或最小值。

典型例子：实时数据流中找中位数。你需要维护两个堆，一个大顶堆存放较小的一半数，一个小顶堆存放较大的一半数，从而动态地获取中位数。

2. 场景：调度与贪心算法

在这类问题中，你需要在每一步都做出当前“最优”的选择，而这个最优选择通常就是优先级最高（值最大或最小）的那个元素。

典型例子：
- 任务调度器：每次从任务队列中选择剩余次数最多的任务来执行，以避免冷却时间。这就需要用一个最大堆来动态维护每个任务的剩余次数。
- 合并K个有序链表：每次需要从K个链表的当前头节点中找出值最小的那个节点。用小顶堆可以高效完成每次的选取操作。

3. 场景：Top K 问题

这是面试中最常见的一类堆的应用。问题通常要求找出前K大或前K小的元素。

找前K大：维护一个大小为K的最小堆。新元素如果比堆顶（当前第K大的数）大，就替换堆顶并调整。最终堆里的就是最大的K个数。
找前K小：维护一个大小为K的最大堆。新元素如果比堆顶（当前第K小的数）小，就替换堆顶并调整。最终堆里的就是最小的K个数。
典型例子：海量数据中找出频率最高的前K个词。

4. 场景：利用堆优化其他算法（如 Dijkstra 算法）

在一些传统算法中，用堆可以极大地优化其时间效率。

典型例子：Dijkstra 最短路径算法。该算法的核心是在每一步从未确定的节点中选取一个距离起点最近的节点。如果用线性扫描，效率是O(N)。如果用一个最小堆来维护这些节点的当前最短距离，每次取最近节点和更新邻居距离的操作效率可以大幅提升。

总结：什么题目适用？

当你看到题目描述中包含以下关键词时，优先考虑优先级队列（堆）：

“前K个” (Top K)
“最频繁的”
“中位数”
“效率最高” / “调度”
“实时数据流”
“合并K个有序...” (链表、数组等)

本质上，堆就是一个“擂台”，新的元素不断上来挑战当前的冠军（堆顶元素），赢了就留下，输了就走人。 所有符合这种“擂台赛”逻辑的题目，都适合用堆来解决。

题目练习

1046. 最后一块石头的重量 - 力扣（LeetCode）

解法（利用堆）：

算法思路：

其实就是一个模拟的过程：

每次从石堆中拿出最大的元素以及次大的元素，然后将它们粉碎；
如果还有剩余，就将剩余的石头继续放在原始的石堆里面。

重复上面的操作，直到石堆里面只剩下一个元素，或者没有元素（因为所有的石头可能全部抵消了）。

那么主要的问题就是解决：

如何顺利的拿出最大的石头以及次大的石头；
并且将粉碎后的石头放入石堆中之后，也能快速找到下一轮粉碎的最大石头和次大石头；

这不正好可以利用堆的特性来实现嘛？

我们可以创建一个大根堆；
然后将所有的石头放入大根堆中；
每次拿出前两个堆顶元素粉碎一下，如果还有剩余，就将剩余的石头继续放入堆中；

这样就能快速的模拟出这个过程。

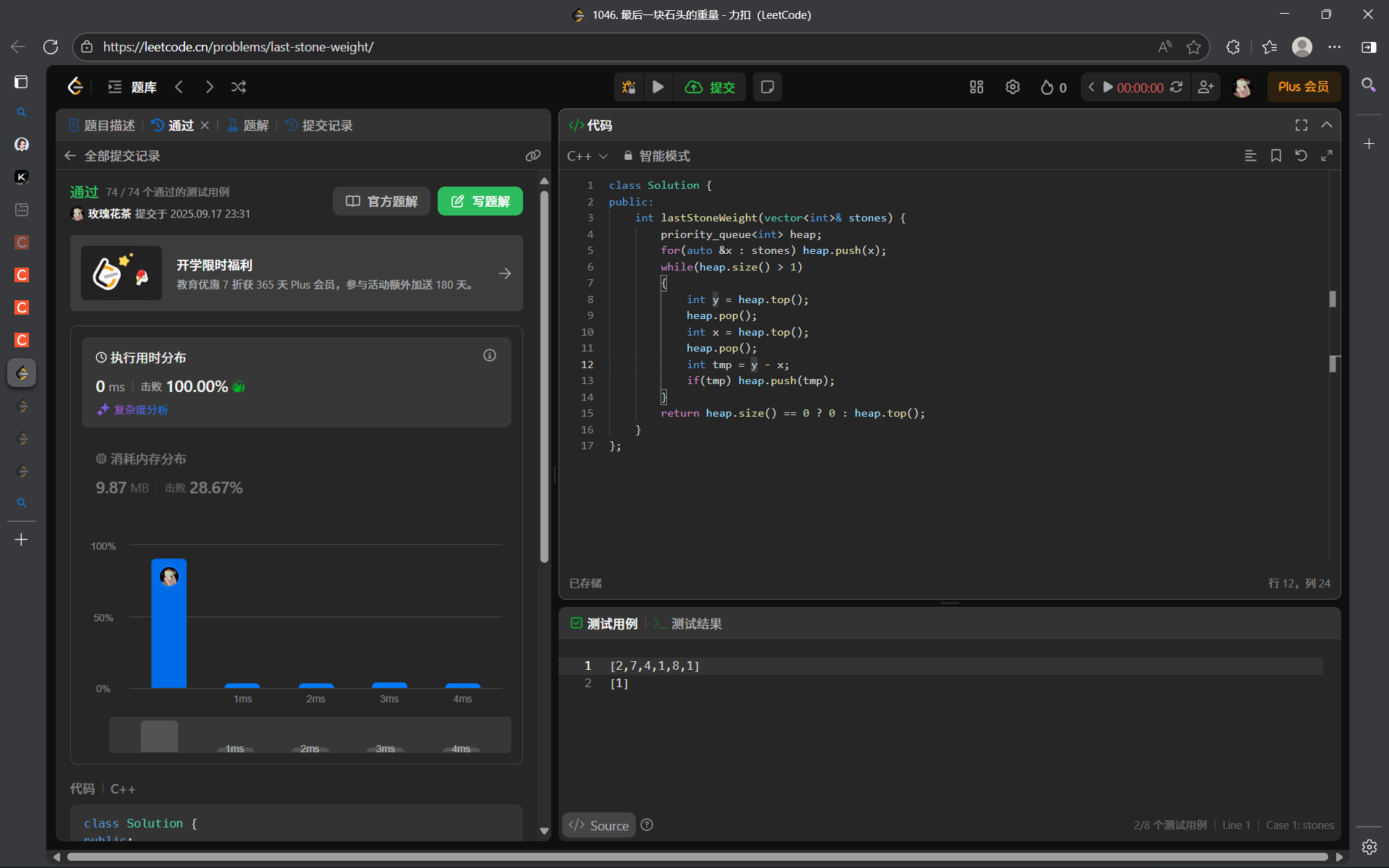
class Solution {
public:int lastStoneWeight(vector<int>& stones) {priority_queue<int> heap;for(auto &x : stones) heap.push(x);while(heap.size() > 1){int y = heap.top();heap.pop();int x = heap.top();heap.pop();int tmp = y - x;if(tmp) heap.push(tmp);}return heap.size() == 0 ? 0 : heap.top();}
};

703. 数据流中的第 K 大元素 - 力扣（LeetCode）

解法（优先级队列）：

算法思路：

我相信，看到 TopK 问题的时候，兄弟们应该能立马想到 「堆」，这应该是刻在骨子里的记忆。

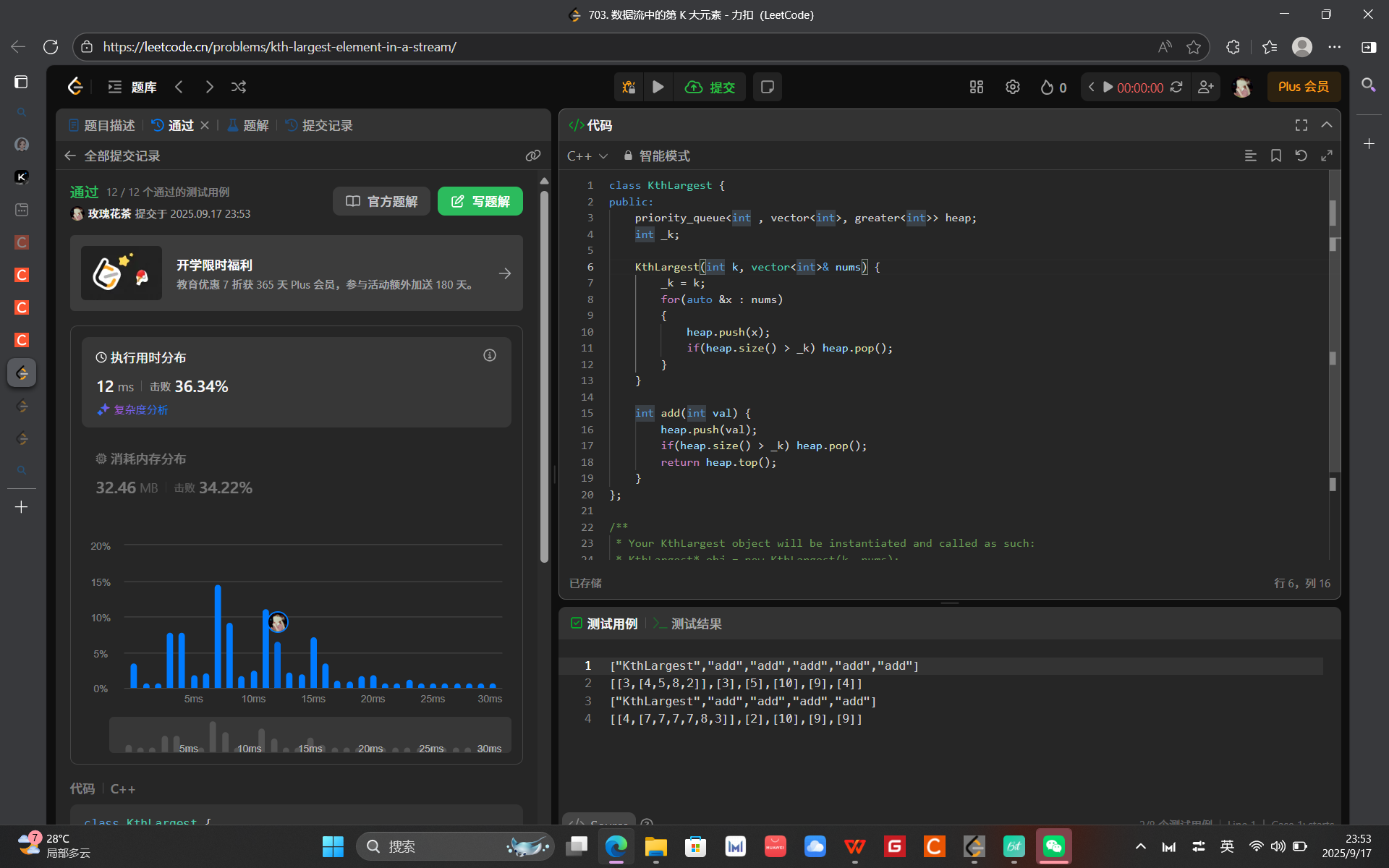
class KthLargest {
public:priority_queue<int , vector<int>, greater<int>> heap;int _k;KthLargest(int k, vector<int>& nums) {_k = k;for(auto &x : nums){heap.push(x);if(heap.size() > _k) heap.pop();}    }int add(int val) {heap.push(val);if(heap.size() > _k) heap.pop();return heap.top();}
};

692. 前K个高频单词 - 力扣（LeetCode）

解法（堆）：

算法思路：

稍微处理一下原数组：
- a. 我们需要知道每一个单词出现的频次，因此可以先使用哈希表，统计出每一个单词出现的频次；
- b. 然后在哈希表中，选出前 k 大的单词（为什么不在原数组中选呢？因为原数组中存在重复的单词，哈希表里面没有重复单词，并且还有每一个单词出现的频次）
如何使用堆，拿出前 k 大元素：
- a. 先定义一个自定义排序，我们需要的是前 k 大，因此需要一个小根堆。但是当两个字符串的频次相同的时候，我们需要的是字典序较小的，此时是一个大根堆的属性，在定义比较器的时候需要注意！
  - 当两个字符串出现的频次不同的时候：需要的基于频次比较的小根堆
  - 当两个字符串出现的频次相同的时候：需要的是基于字典序比较的大根堆
- b. 定义好比较器之后，依次将哈希表中的字符串插入到堆中，维持堆中的元素不超过 k 个；
- c. 遍历完整个哈希表后，堆中的剩余元素就是前 k 大的元素

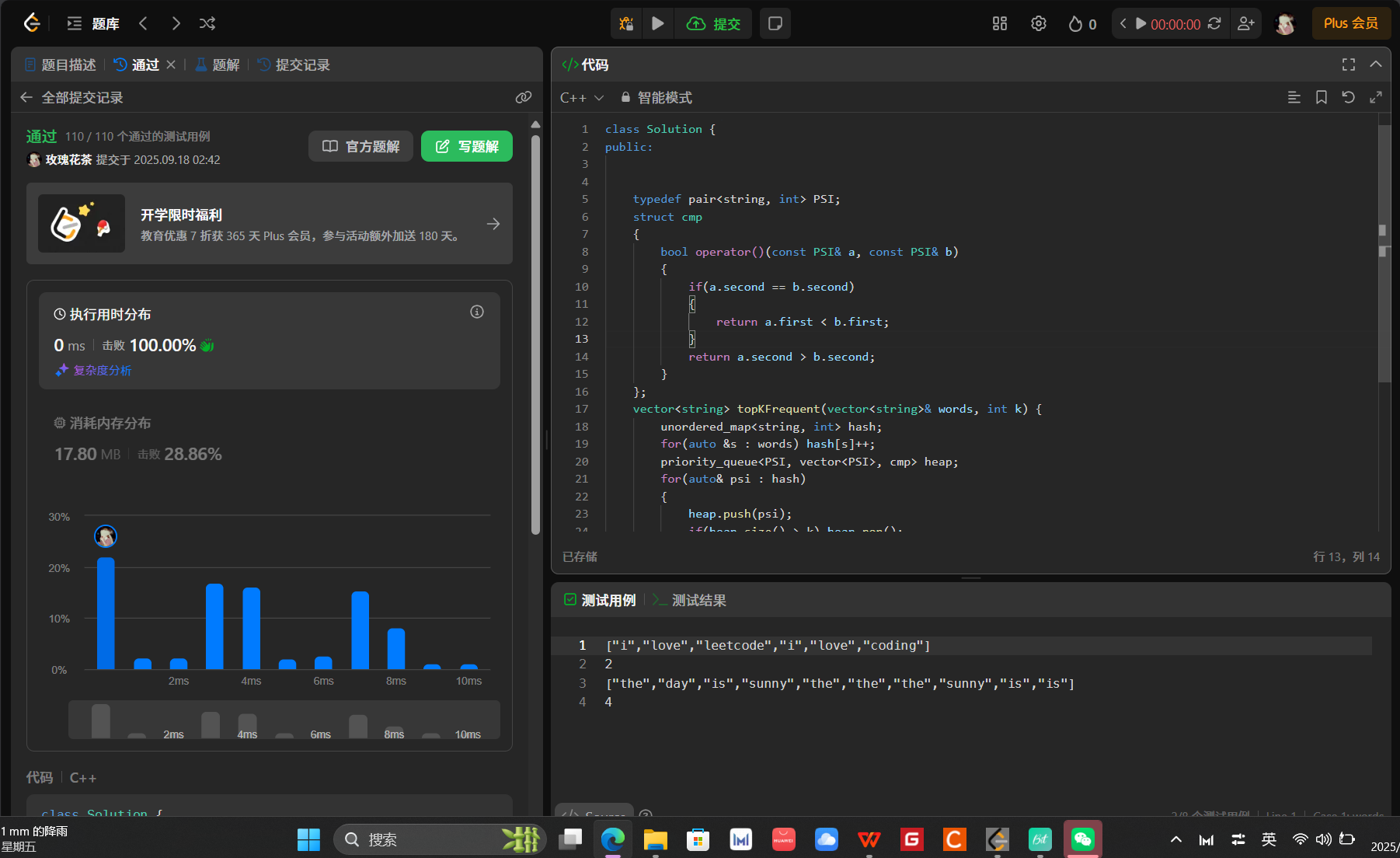
class Solution {
public:typedef pair<string, int> PSI;struct cmp{bool operator()(const PSI& a, const PSI& b){if(a.second == b.second){return a.first < b.first;}return a.second > b.second;}};vector<string> topKFrequent(vector<string>& words, int k) {unordered_map<string, int> hash;for(auto &s : words) hash[s]++;priority_queue<PSI, vector<PSI>, cmp> heap;for(auto& psi : hash){heap.push(psi);if(heap.size() > k) heap.pop();}vector<string> ret(k);for(int i = k - 1; i >= 0; i--){ret[i] = heap.top().first;heap.pop();}return ret;}
};

295. 数据流的中位数 - 力扣（LeetCode）

解法（利用两个堆）：

算法思路：

这是一道关于「堆」这种数据结构的一个「经典应用」。

我们可以将整个数组「按照大小」平分成两部分（如果不能平分，那就让较小部分的元素多一个），较小的部分称为左侧部分，较大的部分称为右侧部分：

将左侧部分放入「大根堆」中，然后将右侧元素放入「小根堆」中；
这样就能在 O(1) 的时间内拿到中间的一个数或者两个数，进而求的平均数。

如下图所示：

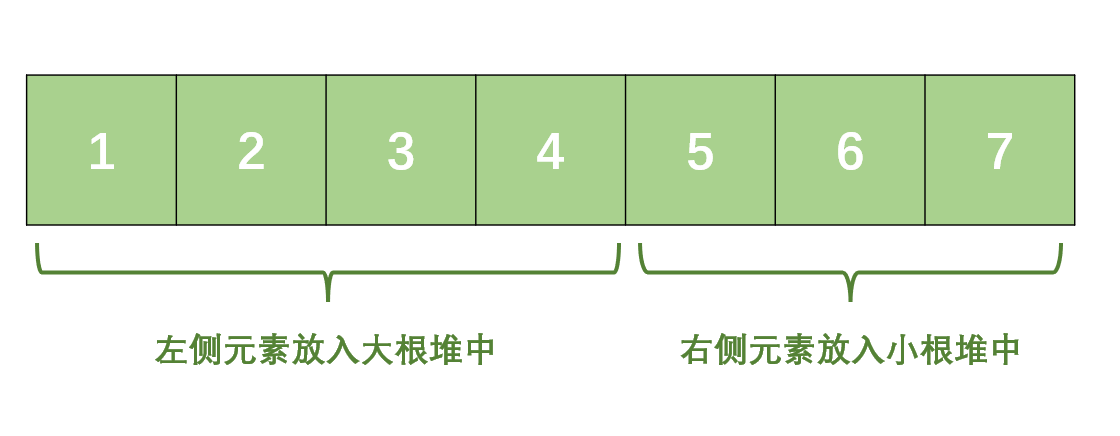
于是问题就变成了「如何将一个一个从数据流中过来的数据，动态调整到大根堆或者小根堆中，并且保证两个堆的元素一致，或者左侧堆的元素比右侧堆的元素多一个」

为了方便叙述，将左侧的「大根堆」记为 left，右侧的「小根堆」记为 right，数据流中来的「数据」记为 x。

其实，就是一个「分类讨论」的过程：

如果左右堆的「数量相同」，left.size() == right.size()：
- a. 如果两个堆都是空的，直接将数据 x 放入到 left 中；
- b. 如果两个堆非空：
  - i. 如果元素要放入左侧，也就是 x <= left.top()：那就直接放，因为不会影响我们制定的规则；
  - ii. 如果要放入右侧：
    - 可以先将 x 放入 right 中，
    - 然后把 right 的堆顶元素放入 left 中；
如果左右堆的数量「不相同」，那就是 left.size() > right.size()：
- a. 这个时候我们关心的是 x 是否会放入 left 中，导致 left 变得过多；
  - i. 如果 x 放入 right 中，也就是 x >= right.top()，直接放；
  - ii. 反之，就是需要放入 left 中：
    - 可以先将 x 放入 left 中，
    - 然后把 left 的堆顶元素放入 right 中；

只要每一个新来的元素按照「上述规则」执行，就能保证 left 中放着整个数组排序后的「左半部分」，right 中放着整个数组排序后的「右半部分」，就能在 O(1) 的时间内求出平均数。

class MedianFinder {
public:priority_queue<int> left;priority_queue<int, vector<int>, greater<int>> right;MedianFinder() {}void addNum(int num) {if(left.size() == right.size()){if(left.empty() || num <= left.top()) left.push(num);else{right.push(num);left.push(right.top());right.pop();}}else{if(num <= left.top()){left.push(num);right.push(left.top());left.pop();}else right.push(num);}}double findMedian() {if(left.size() == right.size()) return (left.top() + right.top()) / 2.0;else return left.top();}
};

查看全文

http://www.dtcms.com/a/390048.html