当前位置：首页 > news >正文

深度学习调参核心：PyTorch学习率调整策略全解析（一）（附系列PPT关键要点）

news 2025/9/19 8:49:07

引言（对应第1张图）

一、梯度下降与学习率：模型训练的底层逻辑（对应第2张图）

1.1 梯度下降的数学本质

1.2 学习率的“双刃剑”特性

1.3 调整学习率的两种方式

二、PyTorch学习率调整框架：三大类策略总览

三、有序调整：按计划“精准降学习率”

3.1 等间隔调整：StepLR

3.2 多间隔调整：MultiStepLR

3.3 指数衰减：ExponentialLR

3.4 余弦退火：CosineAnnealingLR

四、自适应调整：按指标“智能降学习率”

4.1 ReduceLROnPlateau核心逻辑

4.2 实战示例

五、自定义调整：用Lambda函数“自由定制”

5.1 LambdaLR核心原理

5.2 实战案例

六、实战建议：如何选择调整策略？

6.1 初始学习率设定

6.2 策略选择流程

6.3 监控与调试

总结

引言

在深度学习模型训练中，无论是训练一个简单的MNIST分类模型，还是复杂的GPT大语言模型，学习率（Learning Rate）都是优化算法的核心参数，被誉为"优化算法的心脏"。

学习率是一个需要谨慎权衡的参数，它直接决定了参数更新的步长，过大会导致震荡发散，过小则陷入局部最优或收敛过慢。

本文基于系列技术资料，深入解析学习率的理论基础、PyTorch提供的三大类调整策略（有序/自适应/自定义），并通过代码示例与可视化曲线展示实战应用技巧，助您掌握这一影响模型性能的关键超参数。

一、梯度下降与学习率：模型训练的底层逻辑（对应第2张图）

要理解学习率为何需要调整，首先得回到深度学习的核心训练机制——梯度下降。

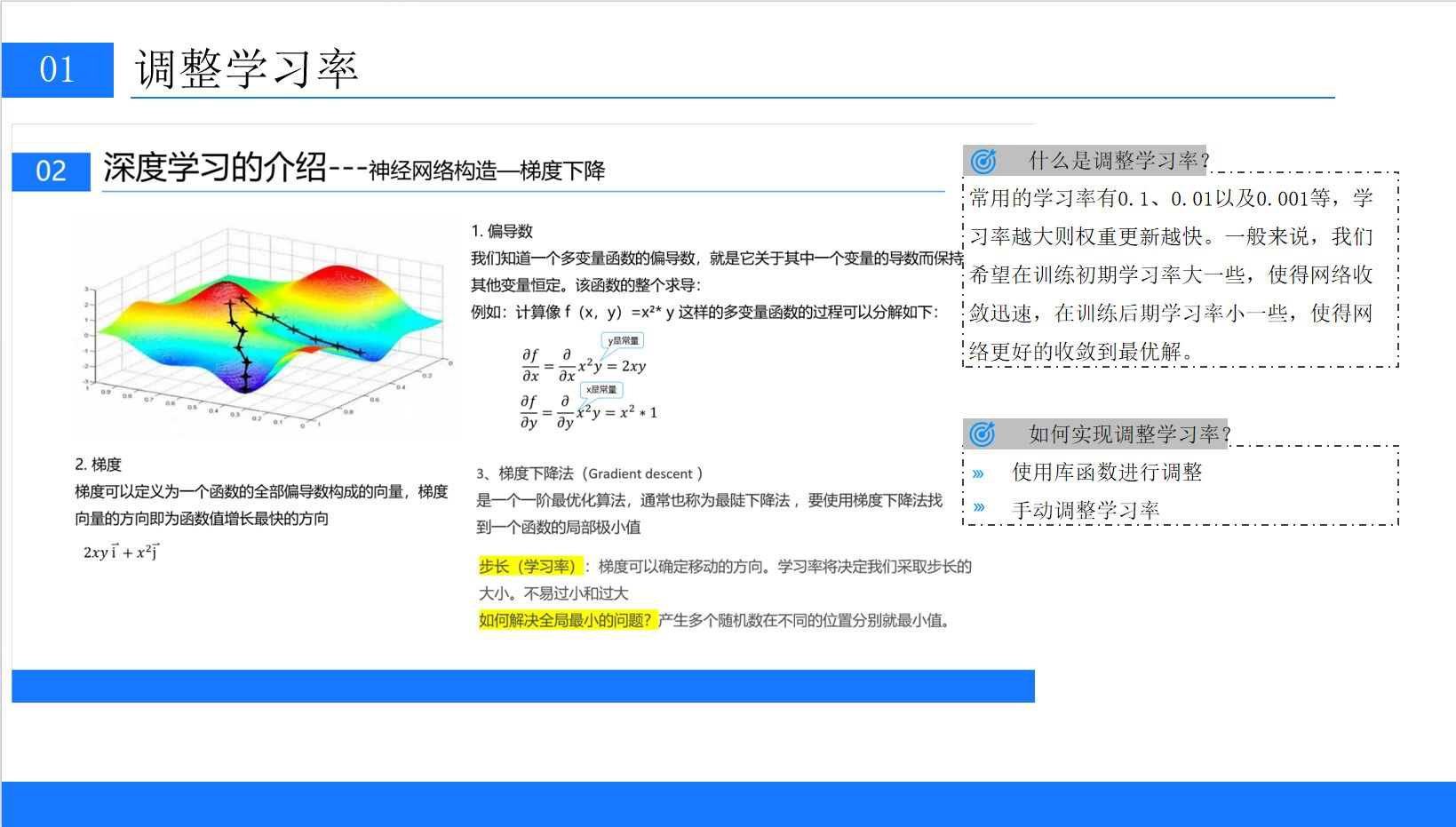
1.1 梯度下降的数学本质

如PPT中的三维彩色曲面图所示（红橙黄绿蓝渐变色曲面），损失函数是一个多维空间的“地形”，我们的目标是找到其最低点（损失全局最小值）。模型参数的更新过程，就像在山坡上寻找下山的最短路径：

偏导数：多变量函数（如损失函数J(θ)）对每个参数的导数，描述了参数变化对损失的影响方向（如函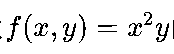数的偏导数）。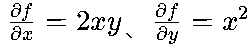
梯度：所有偏导数组成的向量，方向指向损失增长最快的方向（公式为）。
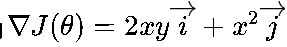梯度下降法：沿梯度的反方向更新参数，公式为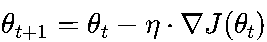，其中η就是学习率，决定了每一步的“步长”。

1.2 学习率------- 一个需要谨慎权衡的参数

学习率的设置需要平衡两个极端：

过大：步长太大，可能直接“跳过”损失函数的最小值，导致训练震荡甚至发散（如在最小值附近反复横跳）。
过小：步长太小，模型需要更长时间才能收敛，甚至可能陷入局部最优（如在平缓区域“原地踏步”）。

应对思路：“希望在训练初期学习率大一些，使得网络收敛迅速；在训练后期学习率小一些，使得网络更好地收敛到最优解。” ------------这正是动态调整学习率的核心目标。

1.3 调整学习率的两种方式

调整学习率有两种主流方式：

手动调整：根据经验或实验结果，在训练过程中人工修改学习率（适合小规模实验）。
库函数自动调整：利用PyTorch等框架提供的接口，自动按预设策略调整学习率（适合工程落地）。

本文将重点讲解PyTorch的库函数自动调整方法，这也是工业界最常用的方案。

二、PyTorch学习率调整框架：三大类策略总览

PyTorch通过torch.optim.lr_scheduler模块提供了灵活的学习率调整接口，支持三大类策略：

策略类型	核心逻辑	典型方法	适用场景
有序调整	按固定周期或epoch节点调整（如每30轮衰减一次、在10/30轮调整）	StepLR、MultiStepLR、ExponentialLR、CosineAnnealingLR	训练过程可预测，需规律性调整
自适应调整	监控训练指标（如验证集损失/准确率），指标停滞时触发调整	ReduceLROnPlateau	数据波动大或需动态响应的任务
自定义调整	通过用户定义的Lambda函数完全控制调整逻辑	LambdaLR	特殊实验需求（如非线性衰减）

接下来，我们逐一拆解这三类策略的具体实现。

三、有序调整：按计划“精准降学习率”

有序调整是最基础的策略，适用于训练过程可预测的场景（如已知模型在50轮后会进入平台期）。PyTorch提供了4种具体方法，我们结合PPT中的函数说明和曲线图详细解析。

3.1 等间隔调整：StepLR

核心逻辑：每经过固定的step_size个epoch，将学习率乘以衰减系数gamma。

函数定义（对应某张PPT的代码示例）：

torch.optim.lr_scheduler.StepLR(optimizer, step_size, gamma=0.1)

optimizer：模型使用的优化器（如SGD、Adam）。
step_size：衰减间隔（单位是epoch，不是iteration！）。
gamma：衰减倍数（默认0.1，即每次衰减为原来的1/10）。

示例：
若初始学习率为0.1，step_size=30，gamma=0.1，则学习率变化为：

第1-29轮：0.1
第30-59轮：0.1×0.1=0.01
第60轮后：0.01×0.1=0.001

曲线特征（如PPT中的折线图所示）：学习率呈阶梯状下降，在step_size的整数倍epoch处出现明显断点。适合需要“阶段性重置”学习率的场景（如模型在初期快速收敛，中期需要更精细调整）。

3.2 多间隔调整：MultiStepLR

核心改进：允许自定义多个关键epoch节点（milestones列表），在这些节点触发学习率衰减，比StepLR更灵活。

函数定义（对应某张PPT的参数说明）：

torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones, gamma=0.1)

milestones：衰减触发的epoch列表（如milestones=[10,30,80]表示第10、30、80轮调整）。

示例：
初始学习率0.1，milestones=[10,30,80]，gamma=0.5，则学习率变化为：

第1-9轮：0.1
第10-29轮：0.1×0.5=0.05
第30-79轮：0.05×0.5=0.025
第80轮后：0.025×0.5=0.0125

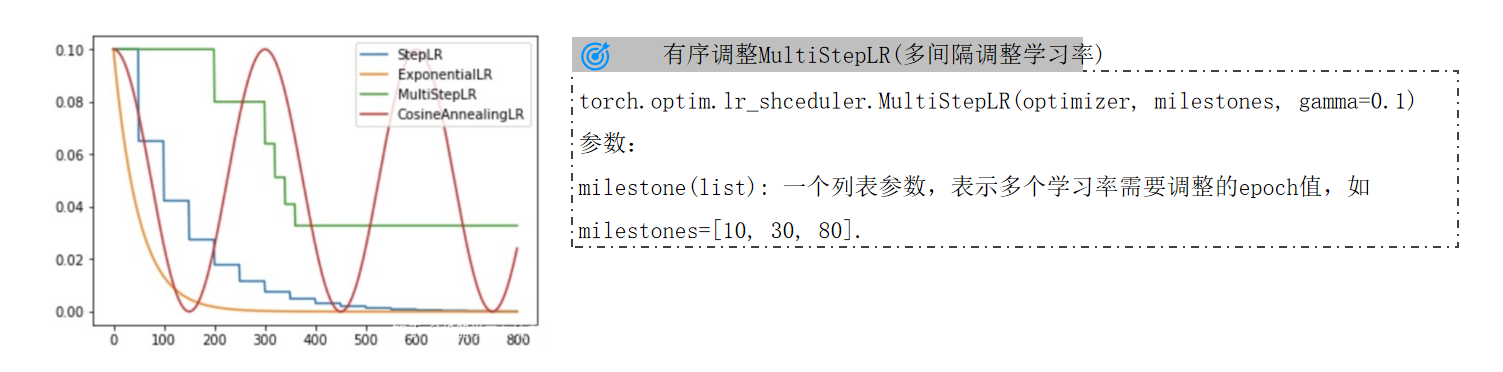
适用场景：当验证集指标在特定轮次（如数据分布变化、模型复杂度提升）出现平台期时，通过milestones精准控制衰减时机（例如CIFAR-10训练中常用[50,100]）。

3.3 指数衰减：ExponentialLR

核心逻辑：每个epoch均按固定比例衰减，学习率连续平滑下降，无阶梯断点。

函数定义（对应某张PPT的参数说明）：

torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma)

gamma：衰减倍数的底数（学习率公式为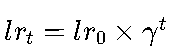，t为当前epoch数）。

示例：
初始学习率0.1，gamma=0.99，则第100轮的学习率为0.1×0.99100≈0.0037。

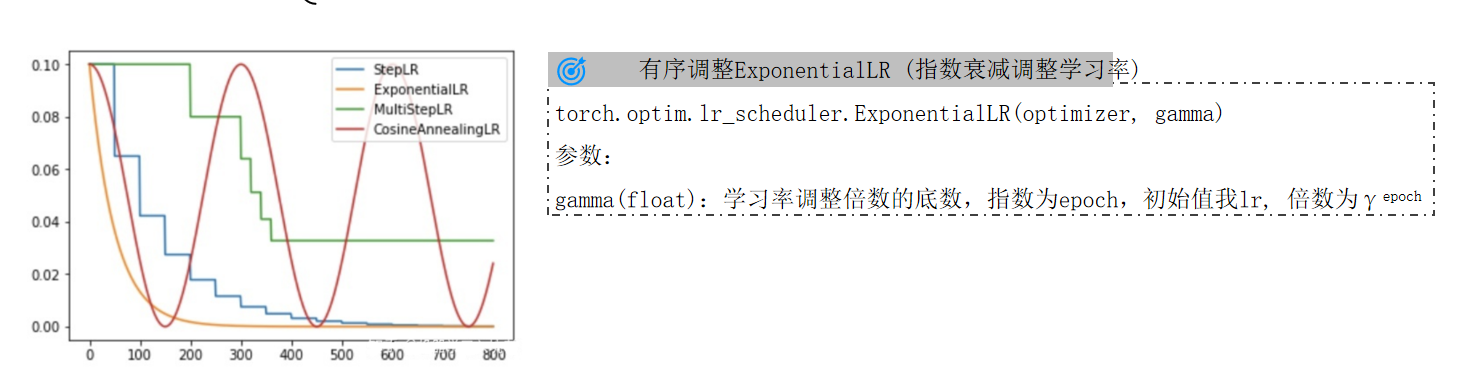
特点（如PPT所示）：

适合需要“持续缓慢衰减”的场景（如超大规模数据集，模型需要长时间微调）。
若gamma接近1（如0.999），衰减极慢，适合训练周期极长的任务；若gamma过小（如0.5），可能导致后期学习率骤降，需谨慎设置。

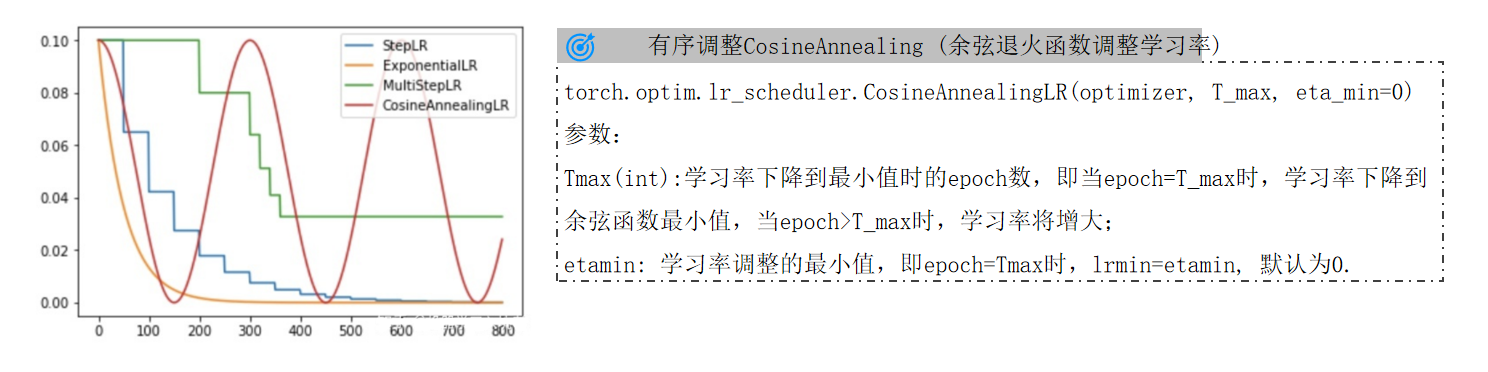
3.4 余弦退火：CosineAnnealingLR

核心创新：模拟余弦函数的周期性变化，学习率先降后升，帮助模型跳出局部最优。

函数定义（对应某张PPT的参数说明）：

torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0)

T_max：余弦周期的长度（单位epoch，一个完整周期为2×Tmax？不，实际是一个完整的余弦半周期，公式中t的范围是[0,Tmax]）。
eta_min：学习率的最小值（默认0，即不会低于此值）。

数学公式（隐含于PPT的曲线图中）：

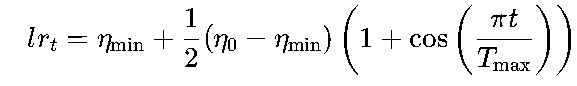
曲线特征（如某张PPT的折线图所示）：学习率呈余弦波形，从初始值平滑下降到eta_min，然后重复（若多次调用step()）。

优势（如PPT中的总结）：

周期性“重启”学习率，帮助模型跳出局部最优（类似“热重启”）。
平滑过渡减少训练震荡，适合非凸损失函数的任务（如CV、NLP中的复杂模型）。

四、自适应调整：按指标“智能降学习率”

有序调整是“按计划”调参，而自适应调整则是“看指标”调参——它通过监控训练过程中的关键指标（如验证集损失、准确率），在指标停滞时自动降低学习率。PyTorch中代表性的方法是ReduceLROnPlateau。

4.1 ReduceLROnPlateau核心逻辑

触发条件：当监控的指标（如验证集损失）在连续patience个epoch内没有改善时，触发学习率衰减。

函数定义：

torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=10, verbose=True)

mode：监控模式，'min'表示关注损失下降，'max'表示关注准确率上升。
factor：衰减倍数（与StepLR的gamma作用相同，默认0.1）。
patience：容忍指标停滞的epoch数（如patience=10表示连续10轮无改善则调整）。
verbose：是否打印调整日志（True时输出“Epoch X: reducing learning rate to XXX”）。

4.2 实战示例

假设我们训练一个图像分类模型，监控验证集损失（mode='min'）：

初始学习率0.01，factor=0.5，patience=5。
第1-5轮：验证损失从0.5降至0.3（持续下降）。
第6-10轮：验证损失稳定在0.29（无改善）。
第10轮结束后：触发调整，学习率降至0.01×0.5=0.005。
第11-15轮：验证损失从0.29降至0.27（重新下降）。

优势：

无需预设固定周期，适应数据分布复杂或波动大的任务（如真实场景中的非平稳数据）。
常与早停（EarlyStopping）配合使用，避免过拟合。

五、自定义调整：用Lambda函数“自由定制”

如果PyTorch内置的策略无法满足需求（如需要非线性衰减、多阶段组合策略），可以使用LambdaLR自定义调整逻辑（对应某张PPT中“可以为不同层设置不同的学习率”）。

5.1 LambdaLR核心原理

LambdaLR允许用户定义一个关于epoch的Lambda函数，学习率由初始学习率乘以该函数的输出值：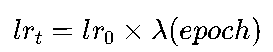

函数定义（示例）：

torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda)

lr_lambda：Lambda函数，输入为当前epoch，输出为学习率缩放因子（可以是任意可计算的函数）。

5.2 实战案例

假设我们需要“前50轮学习率保持0.1，50-100轮线性降至0.01，100轮后保持0.01”，可以定义如下Lambda函数：

lambda_func = lambda epoch: 1.0 if epoch < 50 else max(0.1, 1.0 - (epoch - 50) * 0.001875)  
scheduler = LambdaLR(optimizer, lr_lambda=lambda_func)

前50轮：lambda=1.0，学习率保持0.1。
50-100轮：lambda=1.0 - (epoch-50)*0.001875，例如第75轮时lambda=1.0 - 25 * 0.001875=0.953125，学习率为0.1×0.953125≈0.0953。
100轮后：lambda=0.1，学习率保持0.01。

适用场景（如PPT中的总结）：

非线性衰减需求（如多项式衰减、分段函数）。
多优化器协同调整（为不同参数组设置独立的Lambda函数）。

六、实战建议：如何选择调整策略？

结合系列PPT的经验总结，我们给出以下调参指南：

6.1 初始学习率设定

通用参考：CNN常用0.1/0.01（配合SGD），Transformer常用3e-5/5e-5（配合AdamW）。
快速验证：先用小学习率（如1e-5）测试模型是否收敛，再逐步增大（如1e-3），观察损失下降趋势。

6.2 策略选择流程

优先尝试有序调整：用StepLR或MultiStepLR快速定位合理衰减节奏（如30轮衰减一次）。
复杂任务用自适应调整：若数据波动大（如真实场景图像），改用ReduceLROnPlateau动态响应。
特殊需求用自定义调整：需要非线性衰减或多阶段策略时，用LambdaLR自由定制。

6.3 监控与调试

可视化工具：用TensorBoard或PyTorchViz绘制学习率-损失曲线，观察调整是否有效（理想曲线应是学习率下降后损失持续降低）。
常见问题排查（结合PPT中的调参经验）：
- 训练初期震荡：学习率过大→减小初始值或增大gamma。
- 后期收敛停滞：学习率过小→提高eta_min或改用余弦退火。
- 验证指标波动：调整过于频繁→增大patience或降低factor。