2025年9月17日学习笔记——模式识别与机器学习第11章——非监督学习与聚类

一.引言

1.非监督学习

事先不知道任何样本的类别标号，通过某种算法来把一组位置类别的样本划分成若干类别，这就是非监督模式识别。

2.聚类分析

1.聚类分析即非监督学习模式识别是最典型的非监督学习问题。
2.要使聚类结果有意义，需要对聚类有一定的数学上的要求或假定，这就是聚类的准则。
3.非监督模式识别方法可以分为两类，一类是基于样本的概率分布模型进行聚类划分，如高斯混合模型（书11.2-11.3节）；另一类是直接根据样本间的距离或相似性度量进行聚类，如K均值、模糊k均值，分级聚类等（书11.4-11.6节），还有基于神经网络的聚类划分如SOM模型。

二.基于相似度度量的聚类方法

1.如果不估计样本的概率分布，就无法从概率分布来定义聚类，需要对聚类有其他形式的定义。
2.人们通常根据样本间的某种距离或相似性度量来定义聚类，即把相似地（或者距离近）的样本聚为同一类，而把不相似的（或距离远的）样本归在其他类。
3.分类：动态聚类算法和分级聚类算法

(一)动态聚类算法

1. 动态聚类算法的三个要点：
   （1）选定某种距离度量作为样本间的相似性度量。
   （2）确定某个评价聚类的准则函数。.
   （3）给定某个初始分类，然后用迭代算法找出使准则函数取极值的最好聚类结果。

不同的距离度量方式
1.欧氏距离
2.曼哈顿距离
3.闵可夫斯基距离$dis{t}_{mk}(x,y)=({\sum }_{u=1}^n\mid x_u-y_u{\mid }^p{)}^{\frac{1}{p}}$
4.余弦距离$dis{t}_{\cos }(x,y)=1-\cos (x,y)=1-\frac{x\cdot y}{\Vert x\Vert \Vert y\Vert }$
5.编辑距离
… …

2.特点：多次迭代，逐步调整类别划分，最终使某准则达到最优。

2.1 K均值算法

误差平方和聚类准则

$$J_e=\sum _{i=1}^k\sum _{x\in {\Gamma }_i}{\Vert x-m_i\Vert }^2=\sum _{i=1}^k{J}_i$$
其中${\Gamma }_i$式第i个聚类，$i=1,...,k$，其中样本数为$N_i$，${\Gamma }_i$中样本均值为$m_i=\frac{1}{N_i}{\sum }_{x\in {\Gamma }_i}x$

直观理解：
1.$J_e$反映了用k个聚类中心代表k个样本子集所带来的总误差平方和
2.k均值算法的目标:最小化$J_e$

K均值算法的步骤

（1）初始划分k个聚类，${\Gamma }_i$，$i=1,...,k$，计算$m_j=\frac{1}{|{\Gamma }_j|}{\sum }_{x_i\in {\Gamma }_j}{x}_i\text{和}{J}_e$
（2）对每一个样本$x_i$计算其到各类中心$m_j$的距离${\rho }_{ij}={\Vert \begin{array}{c}{x}_i-m_j\end{array}\Vert }^{2}j=1,\dots ,k$
（3）更新各类集合Γj={xp:ρpj≤ρpl,∀l,1≤l≤k}\Gamma_{j}=\{x_{p}:\rho_{pj}\leq\rho_{pl},\forall l,1\leq l\leq k\}Γj​={xp​:ρpj​≤ρpl​,∀l,1≤l≤k}
（4）重新计算$m_j，j=1,...,k和J_e$
（5）若连续N次迭代$J_e$不改变，则停止；否则转（2）

这是一个局部搜索算法，并不能保证收敛到全局最优解，即不能保证找到所有可能的聚类划分中误差平方和最小的解。算法结果受到初始划分和样本调整顺序的影响。

1.初始代表点选择

（1）凭经验选择代表点
（2）将全部数据随机分成$k$类，计算每类重心。
（3）用"密度法"选择代表点。
（4）按照样本天然的排列顺序或者将样本随机排序后用前$c$个点作为代表点。
（5）从$（c-1）$聚类划分问题的解中产生$c$聚类划分问题的代表点。

2.初始分类方法：

（1）选择一批代表点后，其余的点离哪个代表点最近就归入哪一类，从而得到初始分类。
（2）选择一批代表点后，每个代表点自成一类，将样本依顺序归入与其距离最近的代表点的那一类，并立即重新计算该类的重点以代替原来的代表点。然后再计算下一个样本的归类，直到所有的样本都归到相应的类中。
（3）…

3.关于$k$均值方法中的聚类数目$k$

K均值聚类方法的一个基本前提就是聚类数目$k$是事先给定的，这些在非监督学习问题中并不总是能满足。
（1）根据经验和先验知识确定
（2）根据聚类结构进行估计令$k=1,2,3,...,$求各自的$J_e(k)$找其中的肘点

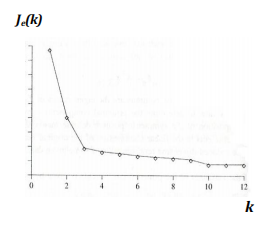
样本中内在聚类不一定很紧密，类别之间并不能很好地分开，或者不同类之间样本分布地紧密程度不同会导致不存在明显肘点。
人们在很多应用中采用地是根据领域知识人为指定类别数目。