小杰机器学习高级(one)——激活函数——sigmoid、tanh、Relu、Leaky Relu、Prelu、ELU、softmax
1.激活函数及其导数算法理论讲解
1.1激活函数论文介绍
024年刚出版的<<激活函数的三十年:神经网络 400 个激活函数的综合调查>>
《Three Decades of Activations: A Comprehensive Survey of 400 Activation Functions for Neural Networks》
包括常用的激活函数和不常用的,400种,大家如果感兴趣可以看看。
THREE DECADES OF ACTIVATIONS A COMPREHENSIVE SURVEY.pdf
1.2激活函数的作用?
激活函数的作用就是在神经网络中经过线性计算后,进行的非线性化。
下面讲解Sigmoid,tanh、Relu,Leaky Relu、Prelu、Softmax、ELU七种激活函数。
1.3激活函数的概念
激活函数给神经元引入了非线性因素,让神经网络可以任意逼近任何非线性函数,
通俗理解为把线性函数转换为非线性函数
1.4 Sigmoid
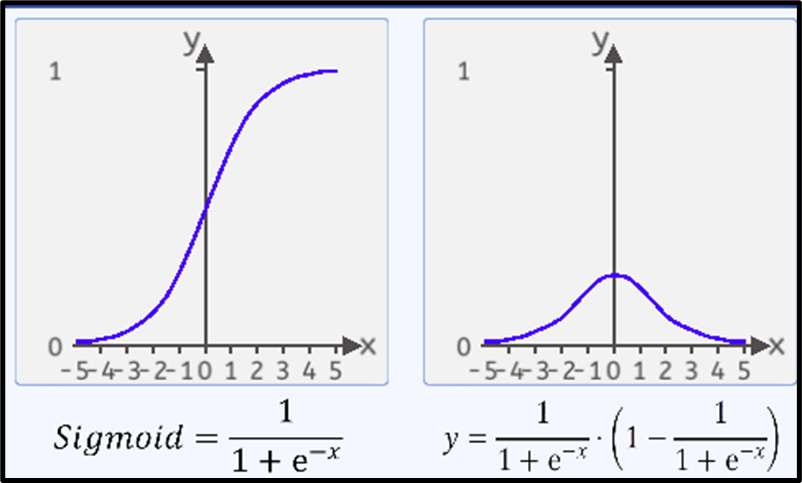
Sigmoid的函数公式为:
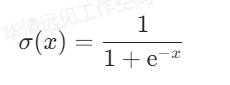
函数图像如下图所示:
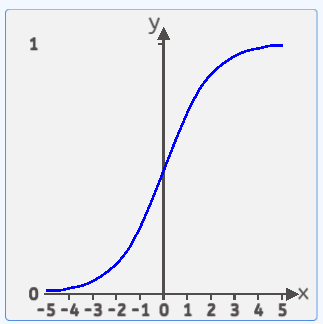
该函数处于(0,1)之间,两边无限接近于0和1,但永远不等于0和1。
sigmoid函数的导数公式为:
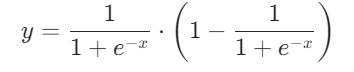
导数图像为:
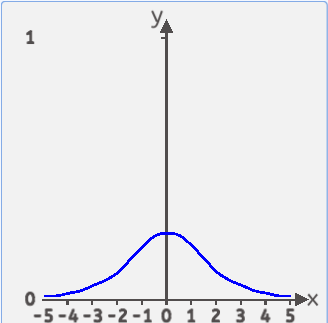
Sigmoid特点总结:
Sigmoid 函数的输出范围被限制在 0 到 1 之间,这使得它适用于需要将输出解释为概率或者介于 0 和 1 之间的任何其他值的场景。
Sigmoid 函数的两端,导数的值非常接近于零,这会导致在反向传播过程中梯度消失的问题,特别是在深层神经网络中。
Sigmoid激活函数有着如下几种缺点:
梯度消失:Sigmoid函数趋近0和1的时候变化率会变得平坦,从导数图像可以看出,当x值趋向两侧时,其导数趋近于0,在反向传播时,使得神经网络在更新参数时几乎无法学习到低层的特征,从而导致训练变得困难。
不以零为中心:Sigmoid函数的输出范围是0到1之间,它的输出不是以零为中心的,会导致其参数只能同时向同一个方向更新,当有两个参数需要朝相反的方向更新时,该激活函数会使模型的收敛速度大大的降低.
计算成本高:Sigmoid激活函数引入了exp()函数,导致其计算成本相对较高,尤其在大规模的深度神经网络中,可能会导致训练速度变慢。
不是稀疏激活:Sigmoid函数的输出范围是连续的,并且不会将输入变为稀疏的激活状态。在某些情况下,稀疏激活可以提高模型的泛化能力和学习效率。
不以零中心有什么问题?举例讲解:

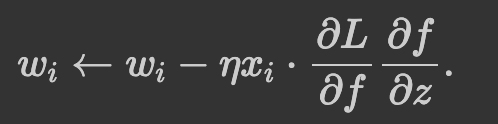
此时,模型为了收敛,w0、w1…改变的方向是统一的,或正或负。所以如果你的最优值是需要w0增加,w1减少,那么不得不向逆风前行的风助力帆船一样,走 Z 字形逼近最优解。如下图所示
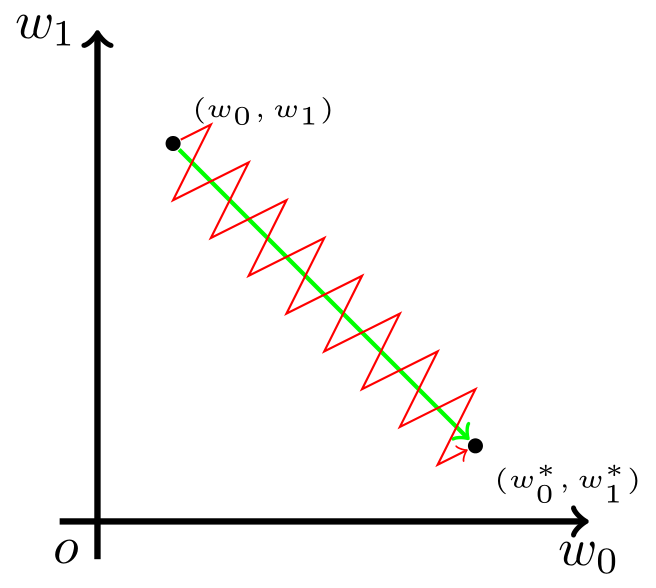
模型参数走绿色箭头能够最快收敛,但由于输入值的符号总是为正,所以模型参数可能走类似红色折线的箭头。如此一来,使用 Sigmoid 函数作为激活函数的神经网络,收敛速度就会慢上不少了。
1.5 tanh
上面了解完Sigmoid函数它的一个特征和代码之后呢,我们来了解一下双曲正切的激活函数tanh。
tanh激活函数的数学公式为
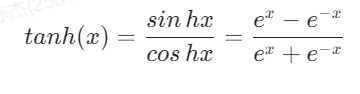
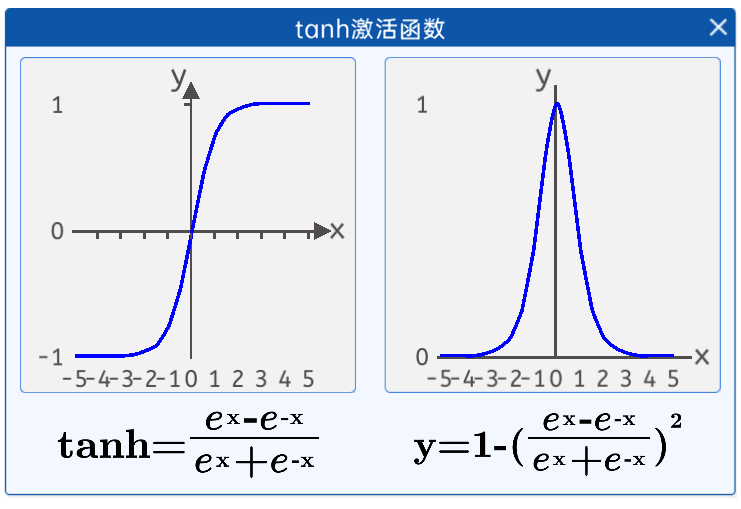
该函数解决了Sigmoid函数不以零为中心的问题,它的取值范围是(-1,1),无限接近1和-1,但永不等于1或者-1,它是关于0中心对称,以零为中心。
tanh导数公式为:
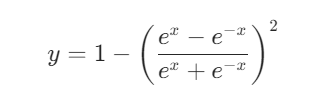
tanh特点总结:
输出范围:tanh 函数的输出范围被限制在 -1 到 1 之间,因此它可以使神经网络的输出更接近于零中心,有助于减少梯度消失问题。
零中心性:tanh 函数的输出以零为中心,即在输入为 0 时函数值为 0,这有助于减少梯度消失问题,并使得神经网络更容易学习。
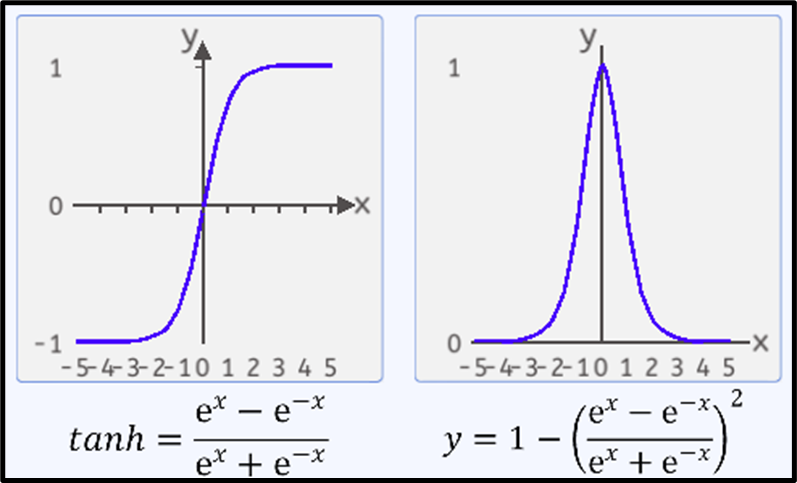
相对于Sigmoid函数,优势显而易见:
输出以零为中心:tanh函数的输出范围是-1到1之间,其均值为零,因此它是零中心的激活函数。相比于Sigmoid函数,tanh函数能够更好地处理数据的中心化和对称性,有助于提高网络的学习效率。
饱和区域更大:在输入绝对值较大时,tanh函数的斜率较大,这使得它在非线性变换上比Sigmoid函数更加陡峭,有助于提供更强的非线性特性,从而提高了网络的表达能力。
良好的输出范围:tanh函数的输出范围在-1到1之间,相比于Sigmoid函数的0到1之间,输出范围更广,有助于减少数据在网络中传播时的数值不稳定性。
但是缺点也同样明显:
容易出现梯度消失问题:虽然相比于Sigmoid函数,tanh函数在非饱和区域的斜率较大,但在输入绝对值较大时,其导数仍然会接近于零,可能导致梯度消失问题。
- 计算难度同样大。
1.6 ReLU
2012年Alexnet提出的激活函数ReLU
ReLU激活函数的数学公式为:
![]()
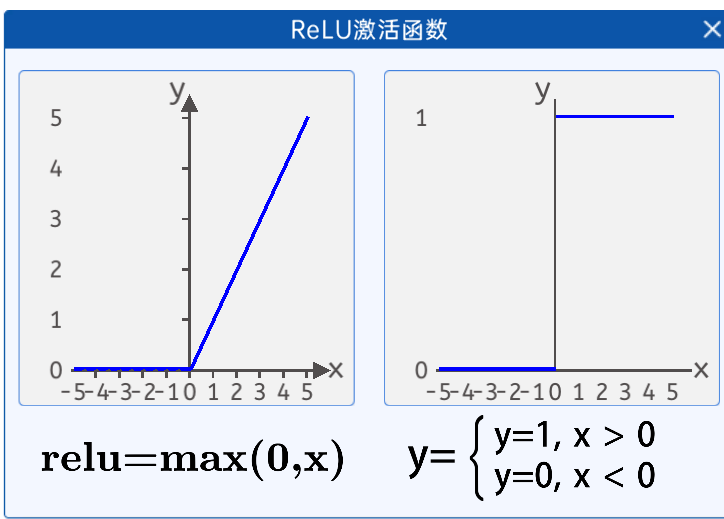
ReLU函数其实是分段线性函数,把所有的负值都变为0,而正值不变。
ReLU函数的导数公式为:
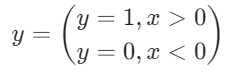
ReLU特点:
稀疏性:ReLU 函数的导数在输入为负数时为零,这意味着在反向传播过程中,只有激活的神经元会传递梯度,从而促进了稀疏激活的现象,有助于减少过拟合。
计算高效:ReLU 函数的计算非常简单,并且在实践中被证明是非常高效的。
解决梯度消失问题: ReLU函数在输入大于零时输出其本身值,这使得在反向传播时梯度保持为常数1,避免了梯度消失问题。ReLU函数在深度网络中更容易训练。
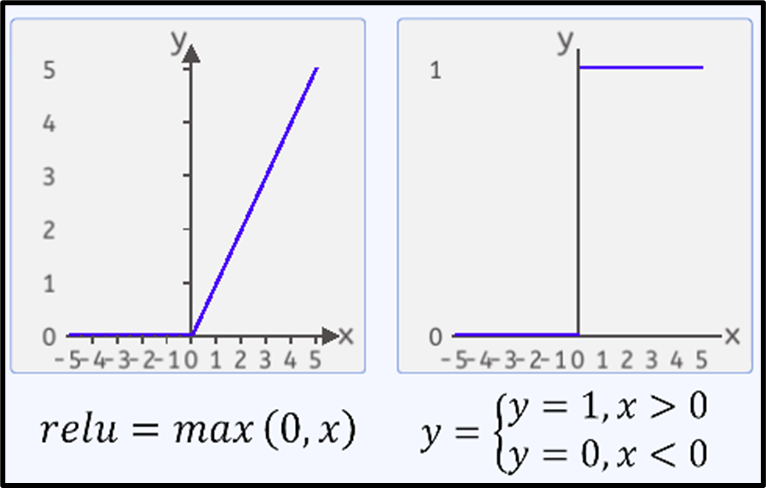
ReLU函数的优势:
- 解决梯度消失问题: ReLU函数在输入大于零时输出输入值,这使得在反向传播时梯度保持为常数1,避免了梯度消失问题。相比于Sigmoid和tanh函数,ReLU函数在深度网络中更容易训练,使得网络能够更有效地学习复杂的特征。
- 计算速度快: ReLU函数的计算非常简单,只需进行一次阈值判断和取最大值操作。这使得在大规模深度神经网络中,ReLU函数的计算速度远快于Sigmoid和tanh函数,加快了模型训练的速度。
- 稀疏激活性: 在输入小于零的情况下,ReLU函数的输出是零,这表现为稀疏激活性。这意味着在激活后,一部分神经元将被激活,而其他神经元则保持不活跃。这有助于减少神经网络中的冗余计算和参数数量,提高了网络的泛化能力。
- 它的劣势:
- 死亡ReLU问题(Dying ReLU): 在训练过程中,某些神经元可能会遇到“死亡ReLU”问题,即永远不会被激活。如果某个神经元在训练过程中的权重更新导致在其上的输入始终为负值,那么它的输出将永远为零。这意味着该神经元不会再学习或参与后续训练,导致该神经元“死亡”,从而减少了网络的表达能力。
- 死亡relu问题理解
-
- ReLU函数梯度只可以取两个值,当输入小于0时,梯度为0;当输入大于0时,梯度为1,在反向传播过程中,
(w新=w旧-学习率*梯度),如果学习率比较大,一个很大的梯度更新后,经过Relu激活函数,可能会导致ReLU神经元更新后的梯度是负数,进而导致下一轮正向传播过程中ReLU神经元的输入是负数,输出是0,由于ReLU神经元的输出为0,在后续迭代的反向过程中,该处的梯度一直为0,相关参数不再变化,从而导致ReLU神经元的输入始终是负数,输出始终为0。即为“死亡ReLU问题”。
- 输出不是以零为中心: ReLU函数的输出范围是从零开始,因此输出不是以零为中心的。这可能会导致训练过程中的参数更新存在偏差,降低了网络的优化能力。
- 不适合所有问题: 尽管ReLU函数在大多数情况下表现良好,但并不是适合所有问题。对于一些问题,特别是在处理一些包含负值的数据时,ReLU函数可能不够理想,可能会产生不良的结果。
针对ReLU函数的劣势,研究人员也提出了一些改进的激活函数,如Leaky ReLU、Parametric ReLU和Exponential Linear Units(ELU)等,这些函数在一定程度上缓解了ReLU函数的问题,并在特定情况下表现更好。因此,在实际使用中,根据具体问题和实验结果选择合适的激活函数是很重要的。
1.7 Leaky Relu
公式:
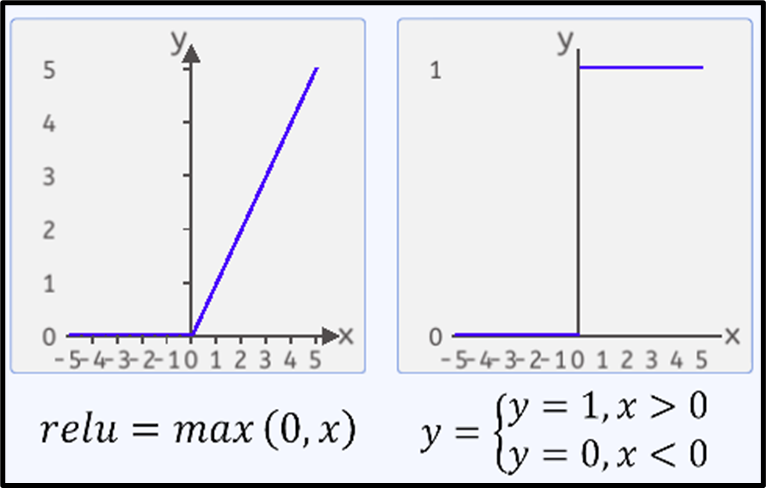
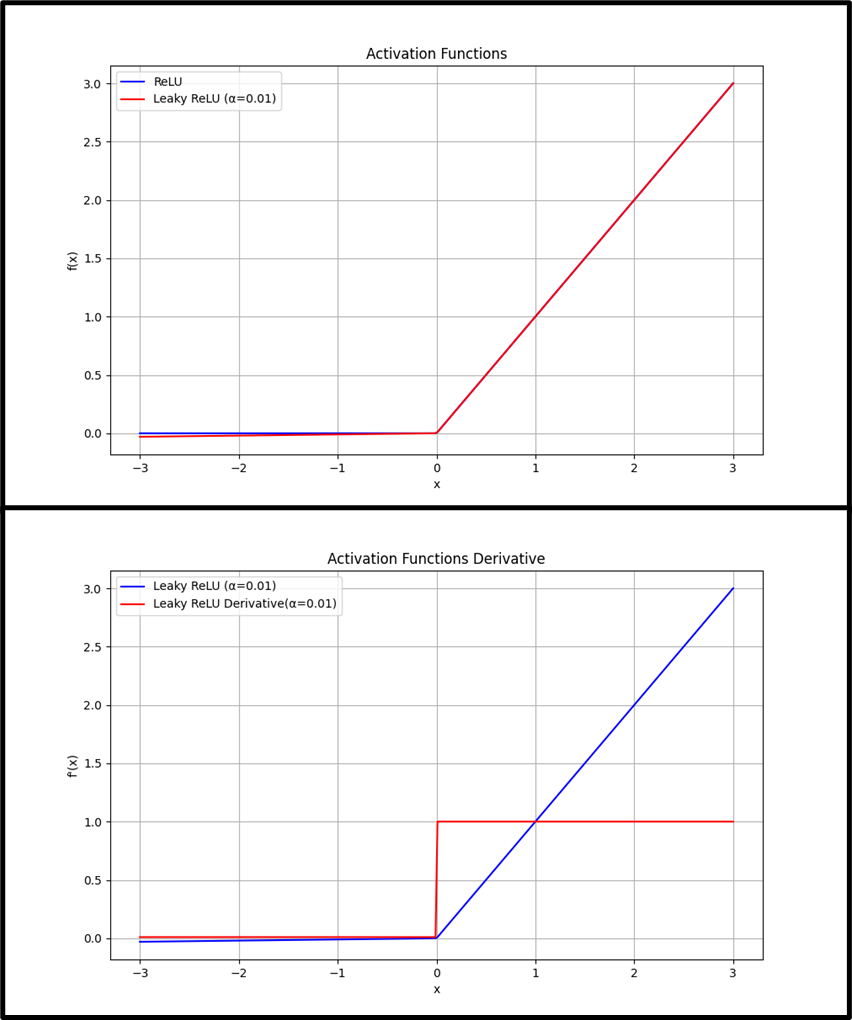
f(x)=max(αx, x),其中 α 是一个小常数(例如0.01)
导数:
f’(x)=1,当x>0时。
f’(x)=α,当x<=0时。
Leaky ReLU 通过在负数区域引入小的正斜率 α 来避免ReLU的“死亡”问题,允许负数区域的梯度不为零。
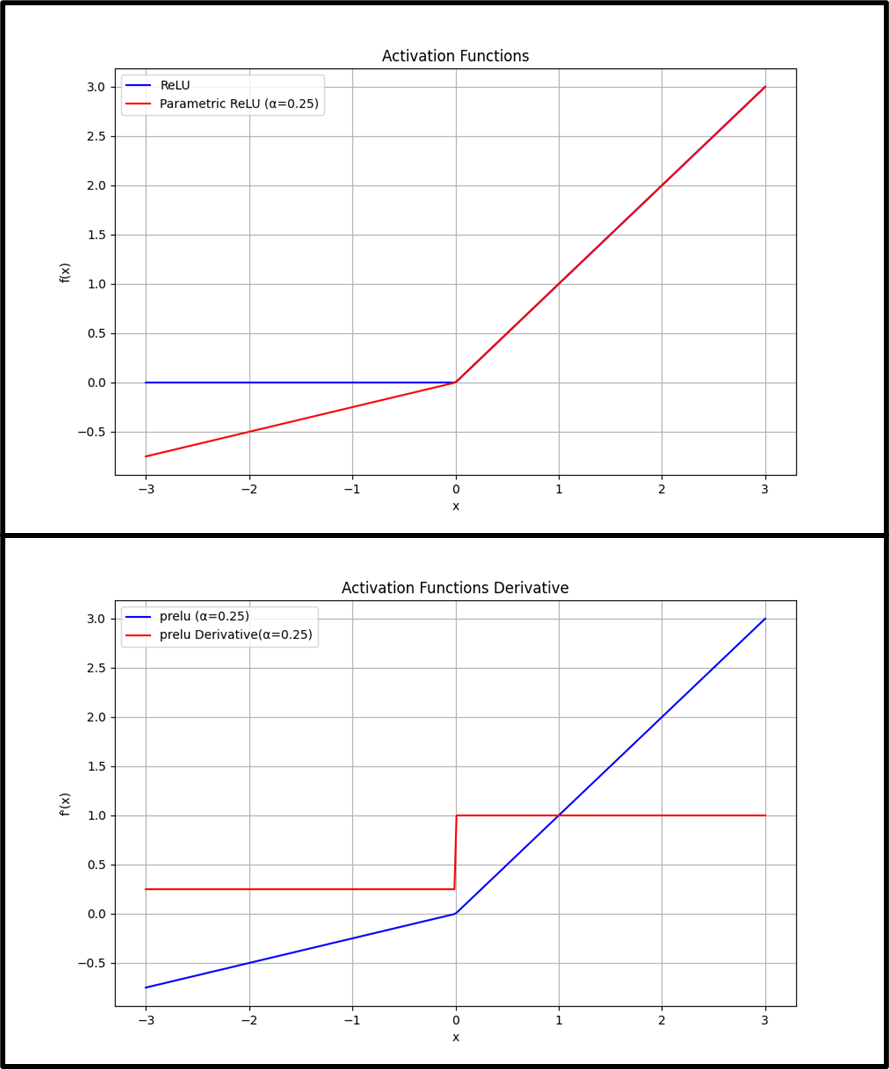
1.8 Prelu
Prelu 和 Leaky Relu想比,Prelu的α是可学习的。
公式:
f(x)=max(αx, x),其中 α 是一个可学习的参数。
导数:
f’(x)=1,当x>0时。
f’(x)=α,当x<=0时。
PReLU是Leaky ReLu的一个变种,其中a是通过学习得到的,这使得模型可以适应性地改变其行为。
1.9 ELU
学习ELU的激活函数。
ELU(Expoentital Linear Unit)激活函数是深度学习中用于增强网络学习能力的又一种激活函数,ELU通过在负值输入时提供负值输出,旨在结合Relu的优点和解决其潜在的一些问题,如ReLU的不活跃神经元问题。
数序定义
ELU函数的数学表达式定义为:
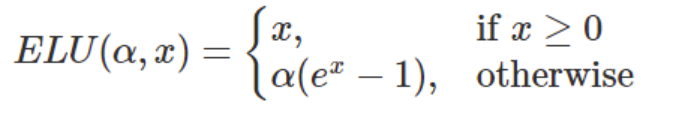
中,x是函数的输入,α是一个预定义的超参数,用于控制x为负值时输出的饱和度。
图像如下:
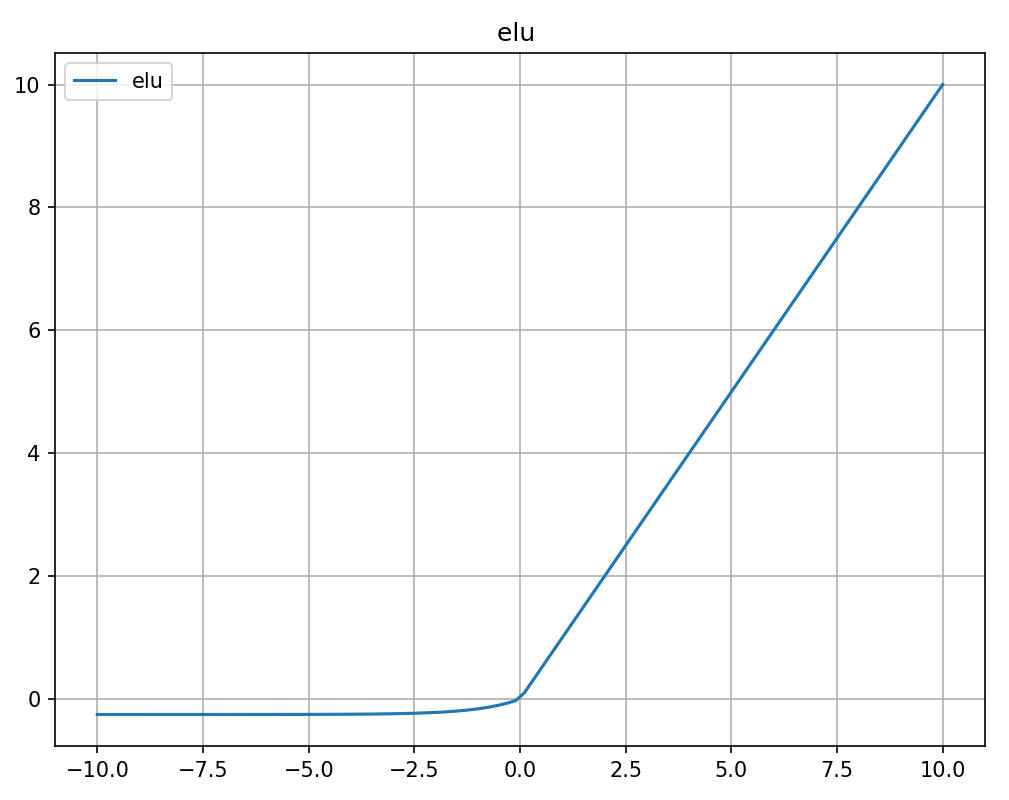
2.函数特性
非线性:ELU是非线性的,可以帮助神经网络学习复杂的数据表示。
连续可导:ELU在整个定义域内连续可导,这有助于提高梯度下降优化算法的稳定性。
解决梯度消失问题:对于负值输入,ELU提供了负值输出,这有助于减轻梯度消失问题,尤其是在深度网络中。
输出均值接近0:ELU函数能够产生负值输出,这意味着其激活输出的均值更接近0,有助于数据的中心化,减少训练过程中的偏置偏移。
3.导数
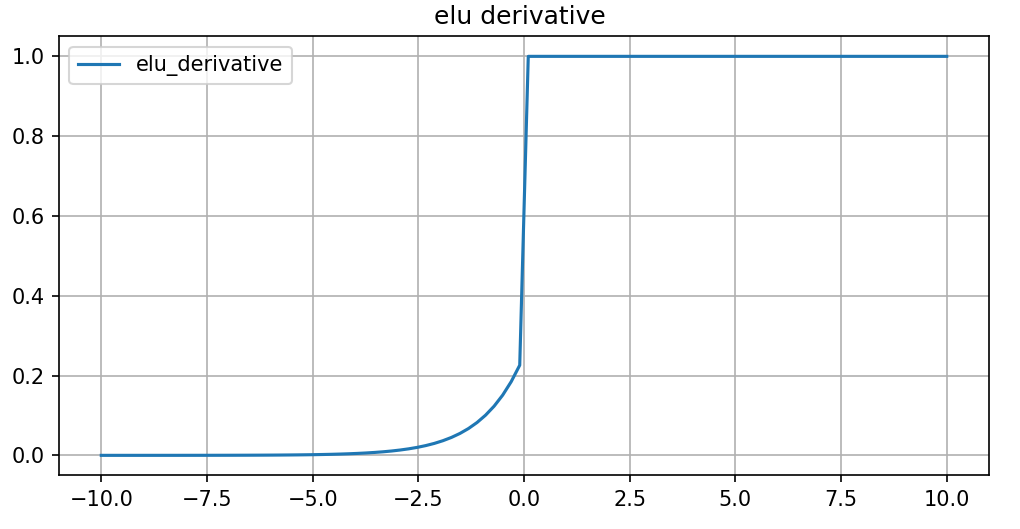
ELU函数的导数如下:
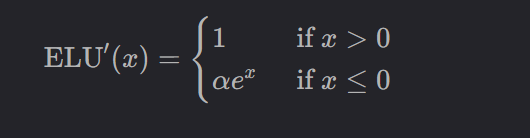
图像如下:
这意味着在正数区域,梯度为1,而在负数区域,梯度取决于α和x的指数值,这有助于保持负输入值的梯度更新。
ELU优势:
ELU通过在负数区域引入指数衰减,能够减少ReLU的“死亡”问题,同时保持负值的输出,有助于保持平均激活接近零,这有助于加快学习。
ELU劣势:
计算成本:由于ELU在负值时涉及指数运算,其计算成本高于Relu及其直接变体,尤其是在前向传播时。
2.0 Softmax
softmax激活函数,但是很多地方,不会把softmax称为激活函数,但是呢没有一个合理的叫法,它就叫softmax函数,但是呢,它的性质上无论和我们的sigmoid或者tanh 或者relu等其实是类似的,我们可以把它称为激活函数。
softmax激活函数为什么不把它称为激活函数,是因为和它的位置是有关系的。为什么呢?
softmax这个函数和我们的sigmoid函数也好。relu函数也好,不一样的点在哪里?sigmoid函数一般位于算法的最后一层,softmax函数它一般只用于最后一次的激活,也就是输出之前的一次激活,前面不用softmax。 softmax一般不用于回归算法中,一般是用于分类中,我们前面计算的都是在算拟合和回归,softmax它做的是分类。
eg:猫和狗,当我们的输出不是一个值而是一个向量的时候,比如要分成三类(猫,狗 ,老虎)三类,根据输出的向量数值,按照下面的公式进行计算。
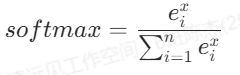
然后再计算后然后再计算损失函数。
Softmax函数,可以将神经网络计算出来的数值通过公式变成概率,经过softmax后得到的结果相加和为1。
另一个优势就是不论向量输出的结果是正值还是负值都能转化为正值。
这个在后续的深度学习中用的非常多。
当n=100时,即有100类时,其图像如下图所示:
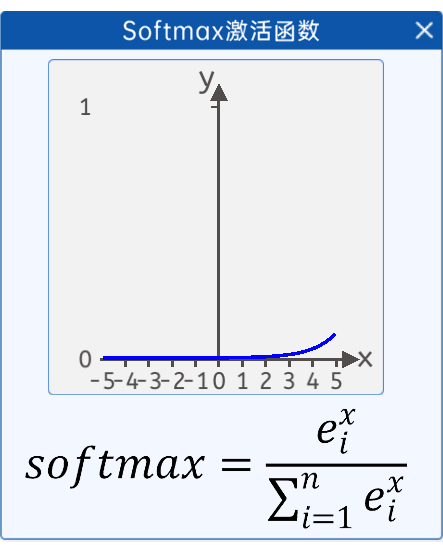
softmax 特点总结:
概率分布:Softmax函数将输入转换为概率分布,因此在多分类问题中常用于将模型的原始输出转换为概率值。
连续可导:Softmax函数是连续可导的,这使得它可以与梯度下降等优化算法一起使用进行训练。
指数增长:Softmax函数中的指数运算可能会导致数值稳定性问题,特别是当输入较大时。为了解决这个问题,可以通过减去输入向量总的最大值来进行数值稳定的计算。
梯度计算简单:Softmax函数的导数计算相对简单,可以通过对Softmax函数的定义进行微分得到。
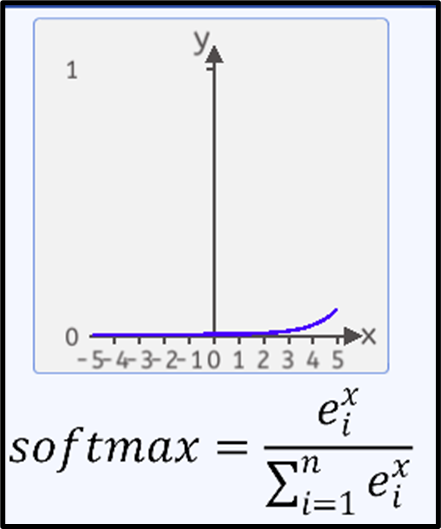
涉及到softmax求导,看一下它怎么求导?



