当前位置：首页 > news >正文

堆排序算法

news 2025/9/18 10:49:50

时间复杂度稳定：始终为O(n log n)
空间效率高：原地排序，O(1)额外空间
适用于大数据集：不会出现快速排序的最坏情况
实现相对简单：基于简单的堆操作

前言

什么是堆排序？

堆排序（Heap Sort）是一种基于二叉堆数据结构的比较排序算法，具有O(n log n)的时间复杂度和O(1)的空间复杂度，是一种高效的原地排序算法

堆的定义

二叉堆是一种特殊的完全二叉树，满足以下性质：

最大堆：每个节点的值都大于或等于其子节点的值

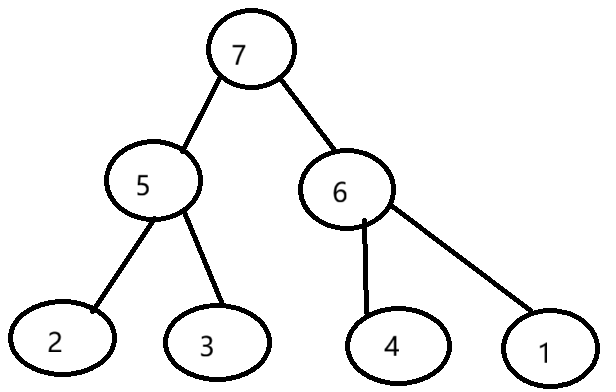
最小堆：每个节点的值都小于或等于其子节点的值

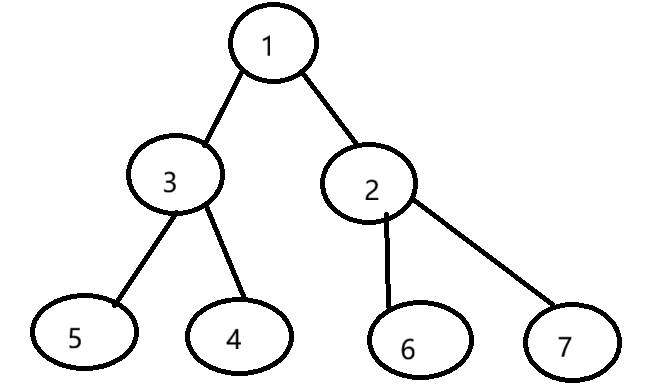
堆的数组表示

堆可以用数组来表示，具有以下索引关系：父节点索引：parent(i) = (i-1)/2,左子节点：left(i) = 2*i + 1,右子节点：right(i) = 2*i + 2;假如数组为[16, 14, 10, 8, 7, 9]

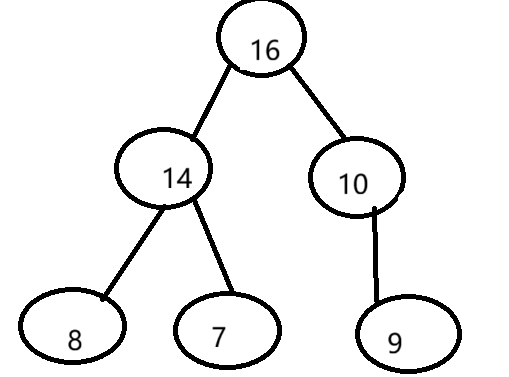
堆排序算法步骤

堆排序分为两个主要阶段：

构建最大堆（Build Max Heap）

将无序数组构建成最大堆。

排序阶段（Heap Sort）

将堆顶元素（最大值）与最后一个元素交换减少堆的大小对新的堆顶元素进行堆化（Heapify）重复上述过程直到堆大小为1；

核心算法：堆化（Heapify）

堆化是维护堆性质的关键操作，其时间复杂度为O(log n)

// 维护最大堆性质
void heapify(vector<int>& arr, int n, int i) {int largest=i;int left=2*i+1；int right=2*i+2;if(left<n&&arr[left]>arr[largest])largest=left;if(right<n&&arr[right]>arr[largest])largest=right;if(largest!=i){swap(arr[i],arr[largest]);heapify(arr,n,largest);}}
}

完整的代码实现

#include <iostream>
#include <vector>
using namespace std;// 堆化函数：维护最大堆性质
void heapify(vector<int>& arr, int n, int i) {int largest = i;        // 初始化最大值为根节点int left = 2 * i + 1;   // 左子节点int right = 2 * i + 2;  // 右子节点// 如果左子节点存在且大于根节点if (left < n && arr[left] > arr[largest])largest = left;// 如果右子节点存在且大于当前最大值if (right < n && arr[right] > arr[largest])largest = right;// 如果最大值不是根节点if (largest != i) {swap(arr[i], arr[largest]);// 递归堆化受影响的子树heapify(arr, n, largest);}
}// 堆排序主函数
void heapSort(vector<int>& arr) {int n = arr.size();// 构建最大堆（从最后一个非叶子节点开始）for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);// 逐个提取元素for (int i = n - 1; i > 0; i--) {// 将当前最大值（堆顶）移到数组末尾swap(arr[0], arr[i]);// 对剩余元素重新堆化heapify(arr, i, 0);}
}// 测试函数
int main() {vector<int> arr = {12, 11, 13, 5, 6, 7};cout << "原始数组: ";for (int num : arr) cout << num << " ";cout << endl;heapSort(arr);cout << "排序后数组: ";for (int num : arr) cout << num << " ";cout << endl;return 0;
}

原始数组: 4 10 3 5 1
堆化索引1(值10): 4/ \10  3/ \
5   1堆化索引0(值4):4        → 交换4和10 →  10/ \                    / \10  3                  4   3/ \                    / \
5   1                  5   1继续堆化:    10  → 交换4和5 →    10/ \                 / \4   3               5   3/ \                 / \5   1               4   1最终最大堆: [10, 5, 3, 4, 1]

交换堆顶10和末尾1: [1, 5, 3, 4, 10]
堆化: [5, 4, 3, 1, 10]
交换堆顶5和末尾1: [1, 4, 3, 5, 10]
堆化: [4, 1, 3, 5, 10]
交换堆顶4和末尾3: [3, 1, 4, 5, 10]
堆化: [3, 1, 4, 5, 10]
交换堆顶3和末尾1: [1, 3, 4, 5, 10]