当前位置：首页 > news >正文

数据结构排序入门（3）：核心排序（归并排序，归并非递归排序，计数排序及排序扫尾复杂度分析）+八大排序源码汇总

news 2025/9/18 8:02:27

1.归并排序

思想：对半分成左右区间，左右区间有序，借助第三个数组tmp。

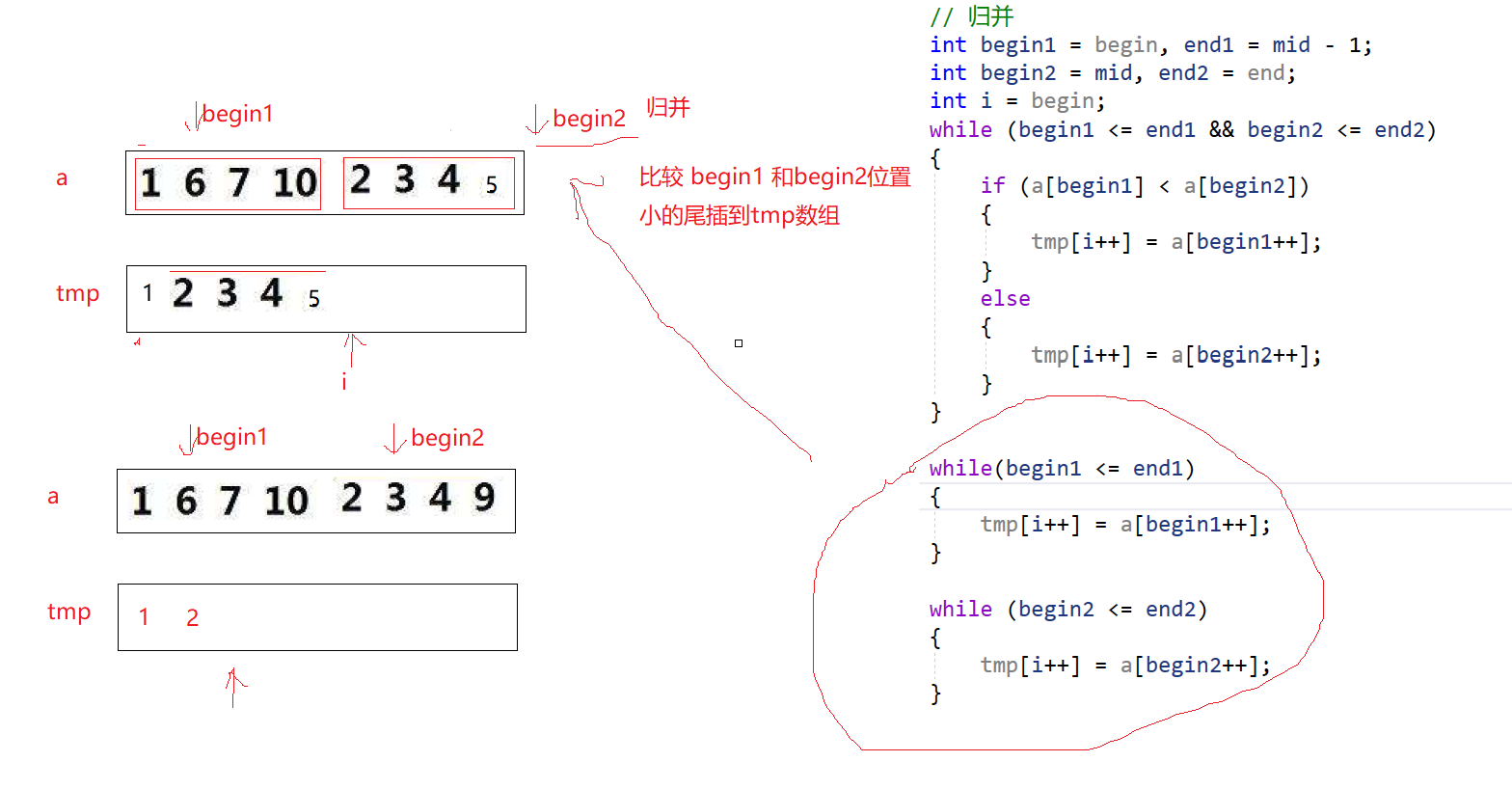
//归并排序
void _MergeSort(int* a, int*tmp, int begin, int end)
{assert(a);//区间中没有元素时不再合并if (begin >= end){return;}//定义一个mid，对半分成两个区间int mid = (begin + end) / 2;_MergeSort(a, tmp, begin, mid);_MergeSort(a, tmp, mid + 1, end);//左右区间明确int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;int i = begin;while (begin1 <= end1 && begin2 <= end2)//两个条件必须同时结束{if (a[begin1] < a[begin2])//如果begin1位置的数据比begin2小，就插入到tmp数组当中{tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];//begin2小于begin1}}//不确定是哪一个先走完,将剩余元素合并到tmp中while (begin1<= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{assert(a);//向内存申请一个数组:tmp,这个数组放置拷贝的数据int* tmp = (int*)malloc(sizeof(int) * n);//拷贝的数据个数跟原数组个数是一样的if (tmp == NULL){perror("malloc fail");exit(-1);}_MergeSort(a, n, 0, n - 1);free(tmp);tmp == NULL;
}

1.1. 归并排序非递归

递归使用会造成时间复杂度的上升，所以优化归并排序，这里可用非递归模式进行。
思想：定义一个gap，gap成2的倍数增加，一个一个归并排成有序数组，gap=1；两个两个归并，gap=2。

//归并排序非递归
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if(tmp==NULL){perror("malloc fail");return;}int gap = 1;while (gap < n)  //gap代表每组归并的个数，当gap>=n的时候，说明循环结束{for (int i = 0; i < n; i += 2 * gap)//第一次gap等于1，第二次gap=2；第三次gap=4依次{int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;// 第二组都越界不存在，这一组就不需要归并if (begin2 >= n)break;// 第二的组begin2没越界，end2越界了，需要修正一下，继续归并if (end2 >= n)end2 = n - 1;int j = i;while (begin1 <= end2 && begin2 <= end2){if (a[begin1] <= a[end1]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}//不清楚是begin1先结束还是begin2先结束while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 < end2){tmp[j++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;//gap呈2的倍数}free(tmp);tmp = NULL;
}

2. 计数排序

思想：将一组数中最大的和最小的数找出来，相减得到数据个数，用这个数据个数申请新的临时数组count（这个临时数组有自然数个下标），将原数组中每个数字出现的个数统计到临时数组count中，然后排序。

//计数排序
void CountSort(int* a, int n)
{//对比出最大的最小的数，相减得到范围int min = a[0], max = a[0];//选择排序for (int i = 1; i < n; i++){if (min > a[i]){min =a[i];}if (max < a[i]){max =a[i];}}int range = max - min + 1;//需要定义一个数组countint* count = (int*)calloc(range, sizeof(int));if (count == NULL){perror("calloc fail");exit(-1);}//统计次数for (int i = 0; i < n; i++){count[a[i]-min]++;//遍历原数组中的每个数据count[a[i]]++//a[i]  原数组，对应a的位置++}//排序int j = 0;//用于返回数组for (int i = 0; i < range; i++){while (count[i]--)//当i的位置是0，后置--，就指向-1{a[j++] = i + min;}}free(count);
}

3. 插入排序，冒泡排序，选择排序，希尔排序，堆排序，快排，归并排序的时间空间复杂度分析汇总

排序空间时间复杂度分析汇总
排序	时间复杂度	空间复杂度
插入排序	O(N ^2)	O（1）
冒泡排序	O(N^2)	O(1)
选择排序	O(N^2)	O(1)
希尔排序	O(N^1.3)	O(1)
堆排序	O(N*log N)	O(1)
快排	O(N*log N)	O(log N)
归并排序	O(N*log N)	O(N)