数据结构七大排序算法模拟实现性能分析

一、引言

排序算法作为数据结构算法中的一个重要内容，其强大的功能性体现为在解决有关大量数据的排序问题表现突出，排序算法不仅在解决有关大量数据的排序问题表现突出，其算法逻辑和思想也都趋近完美。本文将围绕数据结构七大排序算法：冒泡、选择、堆、插入、希尔、快排、归并展开介绍，并模拟实现各自的排序算法，之后对七大排序算法进行性能分析，排序算法模拟实现中我们采取了优化策略，来避免不必要的开销和浪费，算法性能分析包括了一般情况下的时间复杂度分析和最坏情况下的时间复杂度分析。通过学习排序算法，不仅可以很好地帮助我们解决有关大量数据的排序问题，还有助于提高分析解决问题能力，培养算法思想与逻辑思维。

二、冒泡排序

首先我们来介绍最简单、同时也是最基础、重要的排序：冒泡排序。冒泡排序的核心在于两两相邻元素的相互交换，具体过程为每趟冒泡子排序从数组起始位置开始遍历，当数组前一个元素比后一个元素大时，交换二者的值，继续向后遍历，下面的演示具体展示了冒泡排序的过程。

从上图可以看出，单趟冒泡子排序处理的是该趟冒泡排序中最大的数，假设数组有n个数据，当第1趟冒泡子排序完成后，数组中最大的数将移动至数组下标为n-1的位置，同理进行第2趟冒泡排序，数组第二大的数将移动至数组下标为n-2的位置，第3趟冒泡排序完成后，数组第三大的数据移动至数组下标为n-3的位置，以此类推，当第（n-1）趟冒泡排序完成后，此时数组第二小的数移动至数组下标为1的位置，这时数组已经排好了（n-1）个数据，可知此时数组最小的数也将在数组下标为0的位置，因此当第n-1趟冒泡排序完成后，整个数组都有序，不需要再进行第n趟冒泡排序，冒泡排序完成。

代码实现：

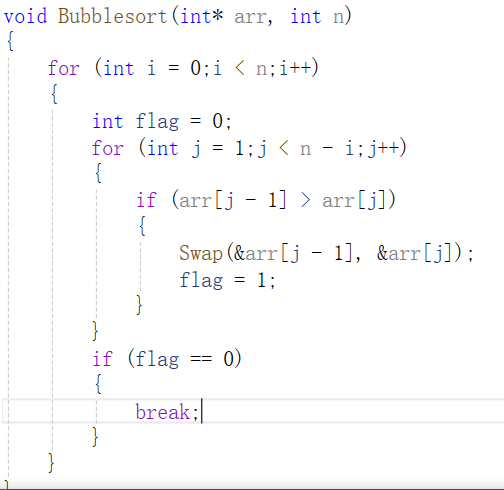
首先，创建一个Swap函数，用于两个数据进行两两交换，由于函数形参的改变影响实参，所以这里需进行传址调用，因此Swap函数参数需为两个数据的地址，即指针，tmp作为两个数据交换的媒介，实现两个数据的交换。冒泡排序Bubblesort函数需利用两层循环，第一层for循环为冒泡排序的趟数，若数组中有n个数据，则冒泡排序的总趟数为n-1，第二层for循环为每趟冒泡子排序的过程，即从数组首元素开始遍历，若前一个元素大于后一个元素，则交换二者的值，继续向后遍历，每趟冒泡子排序完成后，最大元素已到达相应的位置，接下来就无需对该元素进行排序，因此每次冒泡子排序的数据都会减少一个。这里还需注意的是冒泡排序的最大排序趟数为n-1，由上图演示可知，数组完成两趟冒泡子排序后，此时数组已经有序，当数组进行第3趟冒泡排序时，数组元素不会两两进行交换，也就是说冒泡排序可以提前停止，因此我们定义了一个flag标志，用来判断冒泡排序是否可以提前停止，flag初始化为0，当一趟冒泡子排序发生元素的两两交换，flag置为1，当一趟冒泡子排序没有发生元素的两两交换，说明数组已经有序，冒泡排序可以提前停止，flag为0，break跳出循环，从而优化了冒泡排序的趟数。每趟冒泡子排序最大排序次数为n，进行n-1趟冒泡子排序，可知冒泡排序的时间复杂度为O（N^2）,总体而言，冒泡排序并不是一个效率很高的排序，在实践中意义不大，但冒泡排序具有教学意义，是入门排序和算法的不二选择。

三、选择排序

选择排序即对数组进行多次遍历，每次数组遍历中选出遍历数组中的最小与最大值，将最小值置于数组元素的起始位置，最大值置于数组的最后一个位置，下面的演示展示了选择排序的具体过程。

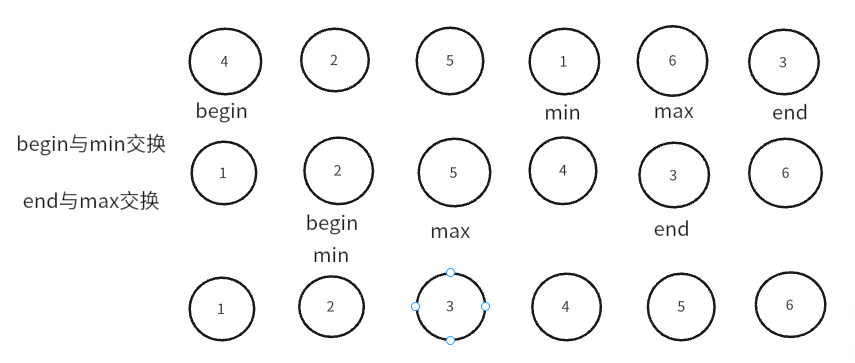
由上图可知，选择排序的每一趟选出遍历数组的最小与最大值，再将最小值与数组begin位置的数据交换，最大值与数组end位置的数据交换，交换完成后，begin++，end--，继续遍历数组[begin,end]的数据，选出最大最小值，再进行交换，直到begin与end相遇，这时数组有序，选择排序完成。

代码实现：

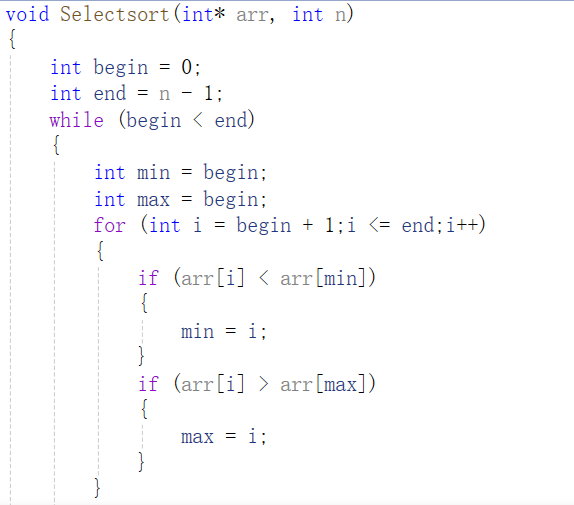
首先begin初始化为0，指向数组第1个元素，end初始化为n-1，指向数组最后一个元素，min、max初始化为begin，之后遍历数组[begin+1,end]的数据，找出最大值的下标max与最小值的下标min，将最小值与begin位置的值交换，最大值与end位置的值交换，交换完成后，begin++，end--，继续遍历数组，选出数组中最大与最小值，继续进行交换，直到begin与end相遇，此时数组已经有序，选择排序完成。

这里需要注意的一点是选择排序中存在一种情况，当begin与max二者相等时，这时先交换begin位置与min位置的数据时，这时max位置的数据就不再是最大值了，最大值变为min位置的值，max的下标需要改变，变为min，可以参考下面这种情形:

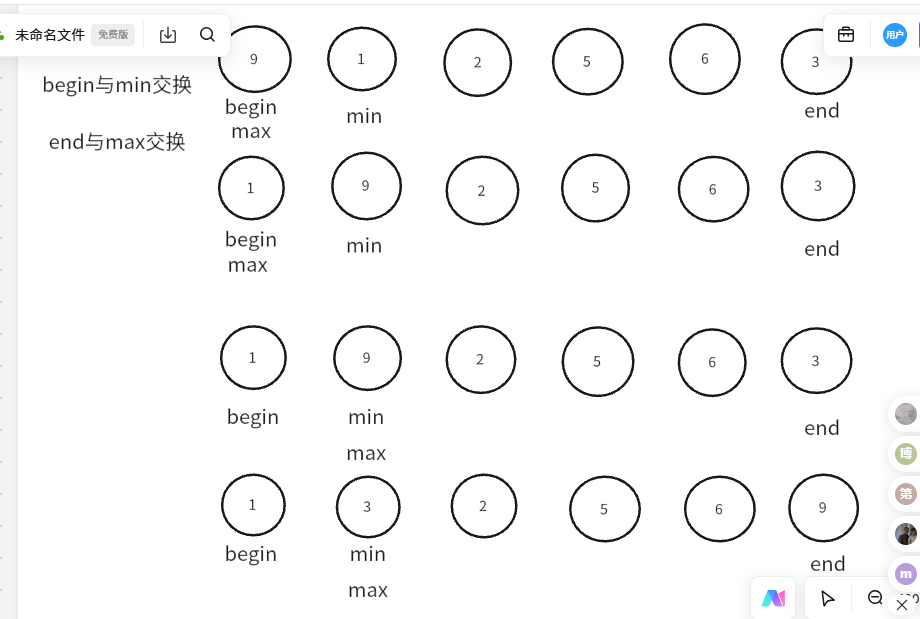
观察上图可知，当第一趟选择排序遍历该数组时，max与begin相等，则交换begin与min位置的值，此时max所指向的值就不再是最大值，而是最小值，此时最大值为min所指向的值，因此这时max也要改变，变为min，指向最大值所在的位置。故针对这种情况，我们需加一步判断，若max与begin相等，则需更新max的值，更新为min，此时max所指向的就是最大值，再将最大值与end位置的值进行交换，完成单趟选择排序。

每趟选择排序遍历n个数据，选择排序的总趟数为n/2，可知选择排序的时间复杂度为O(N^2),选择排序总体的效率还不错，但选择排序是一种不稳定的排序，当数组存在相等的值时，选择排序可能会改变它们的相对位置，例如数组{5,5,2}进行选择排序，排序完成后数组变为{2,5,5}，两个5的相对位置发生变化，因此选择排序是一种不稳定的排序。

四、堆排序

堆排序相比前面冒泡、选择排序在效率上有了很大的提升，堆排序是建立在堆这个数据结构基础上对数组元素采取向下调整建堆，我们对数组进行升序排序，采取建大堆，则数组首元素为数组中最大的元素，如下图：

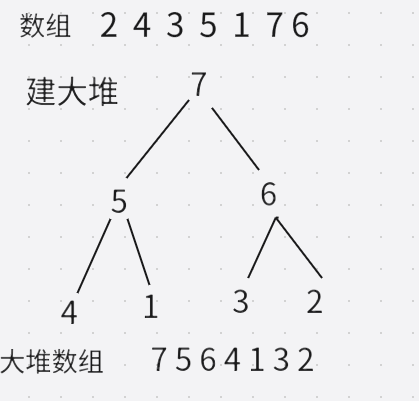
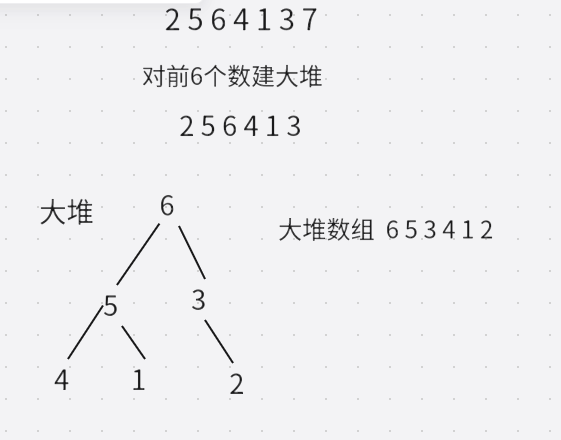
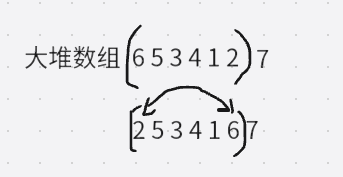
之后交换数组首元素与最后一个元素，此时数组中最大的数就到数组最后一个位置，这时数组最后一个数据已经排好，只需排前面n-1个数据，对前面n-1个数据构建大堆，对数组首元素采取向下调整建堆即可，建完大堆后此时数组首元素为数组第2大的数据，再与数组下标为n-2的数据交换，这样就排好了数组下标为n-1与n-2的数据，继续排前面n-2个数据，同样采取向下调整建堆的方式，即可完成对数组n个数据的升序排序，堆排序结束。

代码实现：

首先我们需创建一个向下调整建堆Adjustdown函数，用于堆数据的向下调整，堆数据的向下调整思路为找到该结点的孩子结点，与孩子结点进行比较，若比孩子结点小，则与孩子结点交换，以此类推，继续向下调整，若结点下标为i，其孩子结点下标分别为2i+1和2i+2，我们先假设左孩子2i+1的值大，然后与右孩子进行比较，取较大的孩子与结点进行比较，while循环条件为child<n，即孩子结点存在，若孩子结点大于该结点，则交换二者的值，继续向下调整，直到孩子结点不存在，就完成了该数据的向下调整。

堆排序Heapsort函数先对数组采取向下调整建堆，从数组下标为n-1的数据的双亲结点开始向下调整，下标为n-1的数据的双亲结点下标为(n-1-1)/2，以此类推，继续找下标为n-2的双亲结点向下调整，直到下标为0，就将数组构建成了一个大堆数组，此时数组首元素为数组中最大的数，将它与最后一个元素交换，此时最大的数已经排好，再对前n-1个数据向下调整建堆，此时数组首元素为数组第2大的数，再与数组下标为n-2的数进行交换，此时就排好了最后两个大的数，以此类推，再对前n-2个数进行向下调整建堆...，即可完成对数组的升序排序，堆排序完成。

堆排序是一种基于堆这种数据结构的一种高效排序，由上述分析可知，当对数组进行升序排序时，我们采取建大堆，进行降序时，采取建小堆，堆排序的排序效率极高，在应对大量数据的排序表现突出，其时间复杂度为O(NlogN),堆的数据结构是在完全二叉树的基础上进行拓展，在完全二叉树中限定了双亲结点与孩子结点的大小关系，若双亲结点大于孩子结点，为大堆，小于则为小堆，因此可知堆排序每次向下调整的深度为该完全二叉树的高度logN，进行n个元素的向下调整，因此堆排序的时间复杂度为O(NlogN),总体而言，堆排序的排序效率较高，且较稳定，受数组的初始化顺序影响较小。

五、插入排序

插入排序也是一种效率较高的排序，插入排序的逻辑为在前面[0,end]已经有序的数组中插入一个数据，若数据小于end位置的数据，则end位置的数据向后移动一位，end--，继续比较end位置的值，若仍小于，则继续向后移动，继续比较，直到数据大于end位置的值，则将该数据插入到数组end+1的位置，从而完成插入排序，下面演示具体展示了插入排序的过程。

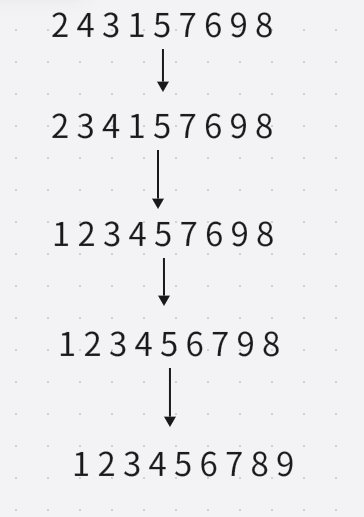
插入排序核心思想是在前面已经有序的数组中插入一个新的数据，上图数组2,4已经有序，将3插入到2,4，步骤为4大于3,4向后移动一个位置，end--，来到2的位置，再将3与2比较，3大于2，则将3插入到end+1的位置，即2的下一个位置，完成了3的插入排序，同理继续遍历该数组，依次完成之后数据的插入排序，数组将会有序。

代码实现：

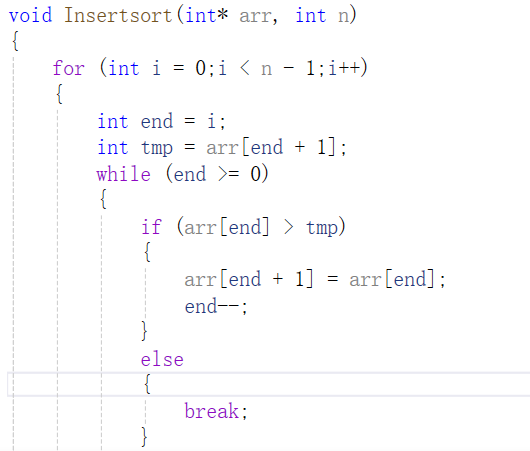
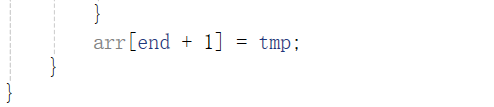
插入排序需两层循环，第一层for循环为插入排序区间的最大长度，可知最后一趟插入排序为在数组下标为[0,n-2]的数组中插入数组最后一个元素，故i最大为n-2，即i<n-1,tmp用于保存要插入的数据，即end+1位置的值，while循环用于插入数据与前面有序数组的依次比较，若插入数据小于end位置的值，则end位置的值向后移动一位，end--，继续比较，直到插入数据大于end位置的值，将该数据插入到end+1的位置，这里也存在一种特殊情况，当插入数据都小于前面有序数组的数据，这时end变为-1，循环不能进去，也就是我们不能在循环中将end+1的值赋值为tmp，因此为了方便，我们统一在循环外将end+1的值赋值为tmp，完成数据的插入排序。

插入排序总体而言是一种效率较高的排序，插入排序的适应性也较强，受数组的初始化顺序影响也较小，插入排序的一趟子排序遍历数据的个数为n，排序的总趟数为n，故插入排序的时间复杂度为O(N^2),插入排序较冒泡排序的效率要高，冒泡排序受数组初始化顺序影响较大，插入排序较稳定，且效率较高，但存在一种情况，当数组中的数据完全逆序时，这时插入排序的效率就明显降低，对于这种情况，我们对插入排序进行了优化，来应对数组逆序的情况，就是下面我们要介绍的希尔排序。

六、希尔排序

希尔排序在插入排序的基础上进行了优化，是插入排序的优化版本，希尔排序的步骤为先对数组进行预排序，预排序的目的是让数组趋于有序，这样就可以很好的应对当数组完全逆序时，插入排序效率不高的情况，对数组预排序之后，再对数组进行插入排序，这样就完成了希尔排序，下面我们来详细介绍预排序的具体过程，预排序的过程也类似于插入排序，进行预排序时，需选定一个gap值，在数组中对相距为gap距离的数据进行插入排序，数组也被分为gap组，每组的数据个数为n/gap个，分别对每组进行插入排序，这就是预排序的过程，下面的演示具体展示了预排序的详细过程。

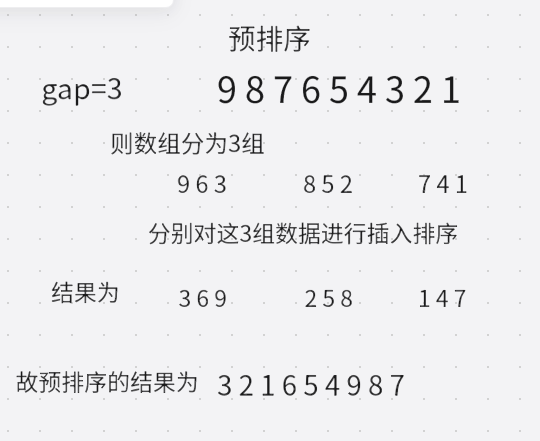
从上图可知，数组{9,8,7，6,5,4,3,2,1}为完全逆序，若对其直接插入排序，则效率不高，我们对其采取预排序后，数组变为{3,2,1,6,5,4,9,8,7}，相比于之前的逆序，这时的数组更趋于有序，再进行插入排序，此时插入排序的效率会有所提高，因此希尔排序是对插入排序的进一步优化。

代码实现：

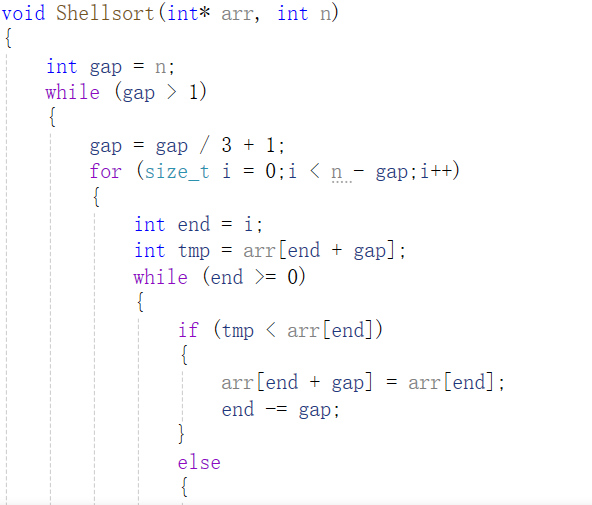
对于希尔排序的预排序过程gap的取值，并没有一个确切的要求，但一般公认的取值为n/3+1，+1的目的是为了使最终gap的值为1，可知当gap=1时，此时的预排序就是插入排序，当gap>1时，为预排序，while循环控制了gap从大于1再变化为1，即代表了预排序和插入排序的过程，for循环执行一次，代表完成了一趟间隔为gap的插入排序，for循环的i++表示多组并着走，即数组被分为gap组，执行完第一组的第一个元素的插入排序后，继续执行第二组第一个元素的插入排序，同时i要小于n-gap，因为i大于n-gap时，此时下一个元素的下标就大于n-gap+gap，即下标大于n，元素越界，下面的while循环即为一趟间隔为gap的插入排序，即预排序，最后gap会变为1，预排序变为插入排序，插入排序完成后，数组将会有序，希尔排序完成。

希尔排序也是一种高效的排序算法，相比于冒泡、选择、插入排序都有很明显的优势，与堆排序旗鼓相当，是对插入排序的进一步优化，希尔排序的时间复杂度不好计算，为O(N^1.3)，涉及到复变函数、概率论的相关内容，每一趟子排序的次数的变化趋势为先增大后减少，总体而言，希尔排序是一种高效的排序算法，其灵活性也较高，受数组初始化顺序影响较小。

七、快速排序

快速排序也是一种高效的排序算法，快速排序的核心逻辑为先在数组中选定一个基准值，再定义两个指向数组头尾的变量，从数组两端向中间遍历数组，左边选出比基准值大的值，右边选出比基准值小的值，然后进行交换，继续重复上面步骤，直到左右两个变量相遇，这时再交换相遇点与基准点的值，此时基准值就会来到排序的最终位置，再以基准值所在的位置为中心，分割出左右区间，对左右区间再执行以上相同的操作，操作完成后，左右区间的数据都将有序，快速排序完成，快速排序的逻辑可类比于二叉树的前序遍历，即先安排基准值的位置，再对左右区间递归进行相同的操作，类似于先遍历根，再遍历左右子树，快速排序的过程可参考下面的演示过程

上图演示的是单趟快速排序的具体过程，以5作为基准值，left，right依次从数组两端开始遍历，right先出发，选出比5小的数，之后left出发，选出比5大的数，再交换left与right的值，交换完成后，right、left继续遍历数组，再进行交换，直到left与right两者相遇，这时二者相遇位置的值必比5小，证明如下：

right与left相遇有以下两种情况，第一种情况是right向前走，与left相遇，此时二者相遇的位置就是left所停留的位置，由于left停留的位置为上次left与right交换的位置，所以该位置的值必比5小。

第二种情况是left向前走，与right相遇，此时二者相遇的位置就是right所停留的位置，由于开始时right先出发，所以left出发前，right已经出发，找到比5小的值而停下，所以二者相遇的位置也必比5小。

此时，交换基准值与两者相遇位置的值，这时5来到了排序的最终位置，5左边的数据都比5小，右边的数据都比5大，同理再对左右区间选出各自基准值，递归进行相同操作，左右区间将有序，整个数组也将有序，快速排序完成。

代码实现：

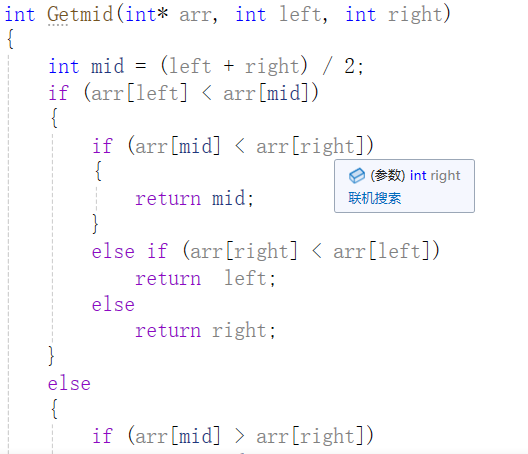
快速排序时间复杂度的计算可类比二叉树的前序遍历，即先排序基准值，再以基准值为中心，分割出左右区间，再分别对左右区间递归进行相同操作，递归的深度即为二叉树的高度logN，递归前遍历数据个数为N，故快速排序的时间复杂度为O(NlogN)，但当数组逆序时，快速排序的效率就会大大降低，此时以数组第一个元素即最大值作为基准值，right在数组最后一个位置，其值比基准值小，不需要移动，这时left向前走，由于数组为逆序，left找不到比基准值大的值，left就会一直走，直到与right相遇，就遍历了整个数组，分割不出左右区间，同理下次遍历也将遍历整个数组，总共将遍历n遍数组，故此时快速排序的时间复杂度就会退化为O(N^2)，因此为了避免上述情况，此时对于基准值的选择也有相关的技巧，我们采取三数取中的方式，Getmid函数用于基准值的选定，步骤为先找出数组中间位置的数据，再将该数据与left、right位置的数据进行比较，找出中间大小的那个数，作为基准值，这样就可以避免因基准值选择不当而导致快排的效率降低，Partsort1函数为单趟快速排序，首先进行三数选中，选出中间值作为基准值，与数组首元素进行交换，while循环中begin找出比基准值大的数据，end找出比基准值小的数据，两者进行交换，直到begin与end二者相遇，再交换相遇点位置的值与基准值，这时基准值的位置就是它在数组的最终位置。Quicksort函数中对左右区间的分割的条件为当区间只有一个数，或者左端点大于右端点，即区间不存在，递归返回。此外，函数中采取了小区间优化策略，当数组元素个数小于10，不再递归，采取插入排序，减少递归的成本，else就是一般情况下的快排，即调用Partsort1函数选出基准值，并对基准值排序，再以基准值为中心，分割出左右区间，再对左右区间递归进行相同操作，递归完成后，左右区间都将有序，整个数组都将有序，快速排序完成。总体而言，快速排序的效率很高，排序中采取三数取中、小区间优化策略，对于快排可谓如虎添翼，快速排序名副其实。

八、归并排序

归并排序也是一种效率很高的排序算法，归并排序可类比快速排序，快速排序的思想可认为是二叉树的前序遍历，那么归并排序的思想可认为是二叉树的后序遍历，归并排序的核心逻辑为数组间两两进行归并，左右两边同时先归并排序两个数据，然后逐渐扩大，归并4个、8个、...n/2个数据，最后将左右两边n/2个数据进行归并，归并完成后，数组将有序，归并排序的具体过程可参考下面的演示：

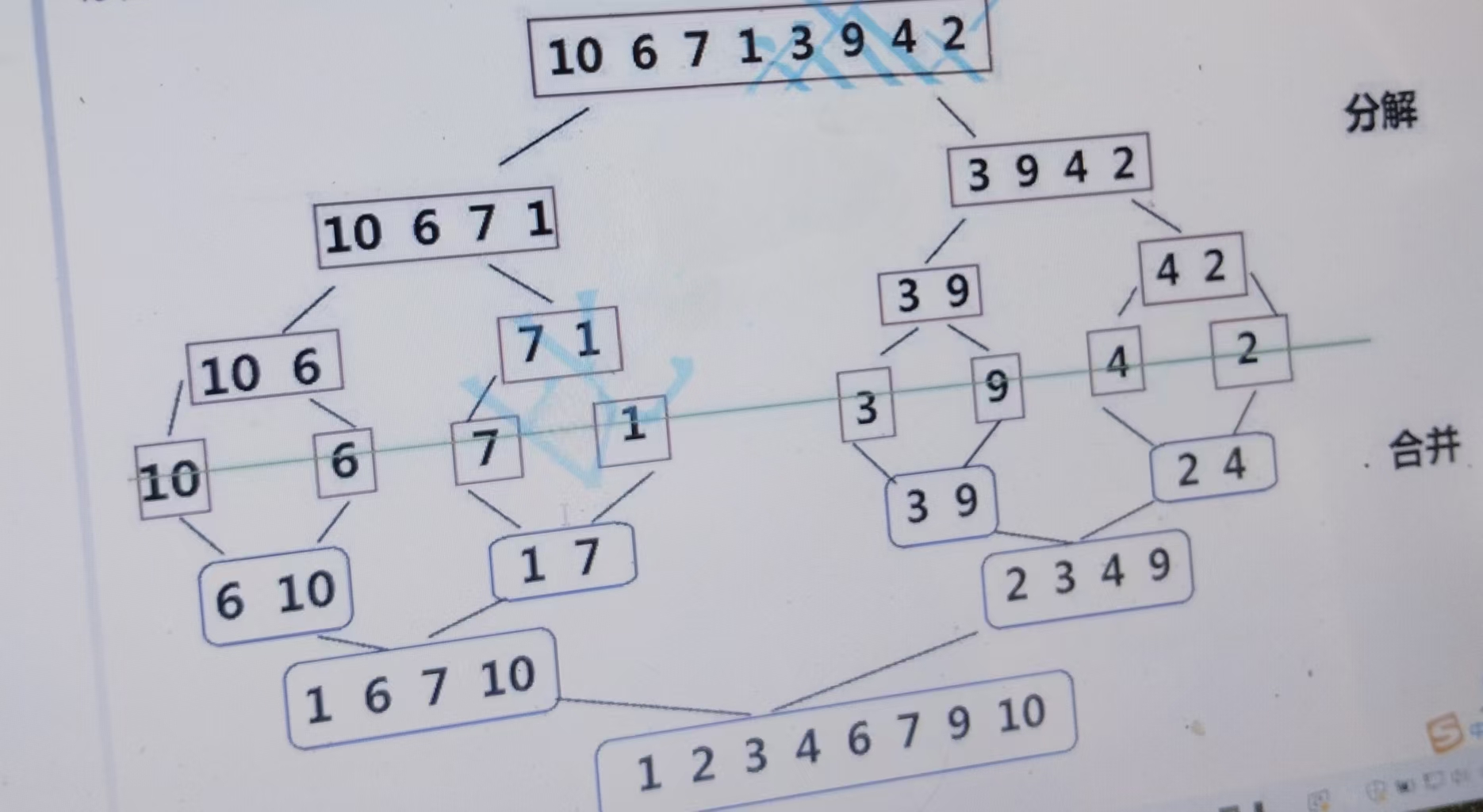
如上图，对数组中的数据先分解，分解方式一般为先分为2组，之后4组，8组...，直到分解为每组只有一个数据，这时开始进行合并，先一一归并排序，再两两归并排序，四四归并，直到n/2个数据与n/2个数据进行归并排序，这时整个数组将有序，归并排序完成。

代码实现：

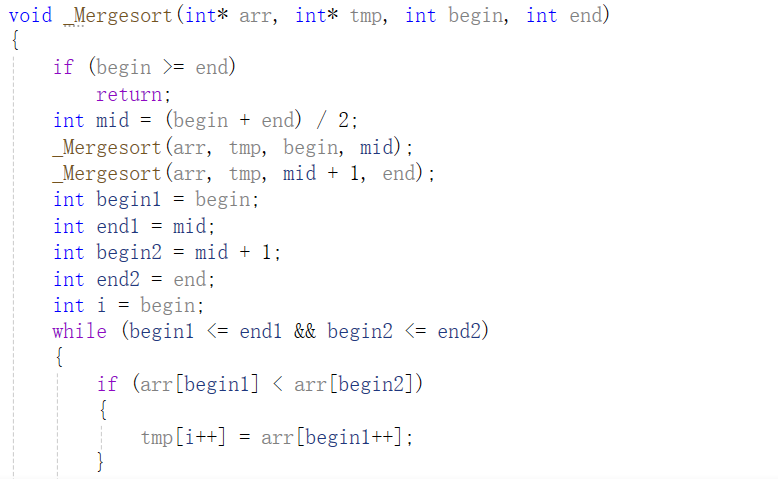
用_Mergesort函数模拟归并排序的过程，递归返回条件同样是当左右区间只有一个数据或者左端点大于右端点时，即区间不存在，递归返回。我们选取数组中间位置的数据，以它为中心，将数组分为左右两个区间，对这两个区间进行归并排序，通过递归方式将区间分解，再合并排序，一趟归并排序的具体过程如下：

先malloc开辟一个tmp数组，然后创建两个指针比较两组归并数组的数据，将小的数据尾插到tmp数组中，并相应移动该指针，继续进行比较，直到数组有一方指针越界，这时就无需进行比较，若一方数组中还有剩余元素，则将剩余元素直接尾插到tmp数组中，最后调用memcpy函数将tmp数组拷贝至arr数组中，完成一趟归并排序。有了前面的_Mergesort函数，归并排序主函数Mergesort只需先malloc申请一块数据个数与arr数组相同的数组空间，然后只需调用_Mergesort函数，即可完成对arr数组的归并排序，最后释放tmp数组，将tmp置为NULL，即可完成归并排序。

归并排序可类比与二叉树的后序遍历，即先排序数组的左区间，类似先遍历二叉树的左子树，再排序数组的右区间，类似再遍历二叉树的右子树，最后将左右区间进行归并，完成归并排序，故归并排序递归的深度为二叉树的高度logN，遍历数组的个数为N，则归并排序的时间复杂度为O(NlogN)。总体而言，归并排序也是一种高效的排序，受数组初始化顺序的影响也较小，其排序的核心思想也是利用递归思想，类似于二叉树的后序遍历，先对数组进行分解，再合并排序，在处理有关大量数据的排序问题时，归并排序也是个不错的选择。

九、结语

以上就是本文有关排序算法的所有内容，本文主要介绍了七大排序算法的核心思想和算法逻辑，其中冒泡和选择排序以数据交换为核心思想，堆排序是基于堆这个数据结构的一种排序算法，堆排序巧妙利用了数据向下调整和交换方法实现对数据的排序，插入排序以数据插入为核心，在前面已经有序的序列中插入一个新的数据，希尔排序是对插入排序的进一步优化，在插入排序前进行了预排序，以此让数组趋于有序，快速排序和归并排序以递归为核心思想，快速排序先选定一个基准值，再对基准值进行排序，之后以基准值为中心，分割左右区间，再对左右区间递归进行相同的操作，类似于二叉树的前序遍历，归并排序则是先对左右区间进行排序，再将左右区间进行合并排序，类似二叉树的后序遍历。掌握七大排序算法以及了解它们各自的算法性能，不仅能很好地帮助我们解决有关大量数据的排序问题，同时也能锻炼我们的算法思想和逻辑思维，当然算法的世界浩瀚无垠，我们可以从理解排序开始，逐步深入更复杂的算法世界！