M：Dijkstra算法求最短路径

.DJ介绍

\;\;\;\;\;\;\;\; $Dijkstra$ 算法又叫做 $DJ$算法（我编的^^）。DJ算法用于求解单源最短路径问题，由荷兰一个叫迪杰斯特拉的高人于1956年提出。该算法适用于带权有向图或无向图，并且所有权重必须为非负值。
\;\;\;\;\;\;\;\; 为什么权值一定要是非负值？为什么每次贪心的选择都是正确的？后面会解释。

List

🍑🍑🍑🍑🍑🍑🍑🍑🍑🍑🍑🍑

1. 最短路算法步骤
2. 具体示例演示最短路求解步骤
3. 证明最短路合理性
4. 代码分段解释
5. 代码汇总

🍑🍑🍑🍑🍑🍑🍑🍑🍑🍑🍑🍑

---

.DJ求路径

\;\;\;\;\;\;\;\;用DJ算法来解决单源最短路问题。单源的意思就是一个源点。具体步骤如下：
（假设有邻接矩阵$g[i][j]=x$ 表示点 $i$ 到点 $j$ 的距离是 $x$.）

1. 初始化源点（一般将源点设为从0开始的点，也就是0）到其余所有点的距离（邻接矩阵）。
   • 用 $d[i]=j$ 表示点 $i$ 到源点（点0）的最短路径是 $j$ ，$d[0]=0$，因为源点到源点本身距离是0。
   • 如果点 $j$ 是源点的邻接点，那么$d[j]=g[0][j]$。如果点 $j$ 不是源点的邻接点，那么$d[j]$=+∞ (也就是正无穷大）
2. 找到数组 $d$ 中最小的值，假设其对应下标为 $x$ ,那么点 $x$ 到源点 最近的距离就是 $d[x]$ (贪心思想！！！！最重要的）。
   • 用一个额外的数组 $vis$ 将 $x$ 点标记，即$vis[x]=true$，表示此点找到了到源点的最短路径，后续不能参与操作2。
3. 松弛操作，因为点 $x$ 的最短路径找到了（且是第一次），那么接着通过 $x$ 去更新（松弛）到其他所有邻接点的最短路径。
   • 假设 $x$ 的邻接点是 $y$，那么如果 $y$ 没有被标记$（vis[y]!=true）$，就尝试更新。$d[y]=min(d[x]+g[x][y],d[y])$。
   • 如果 $y$ 被标记$（vis[y]==true）$，就不需要更新，为什么呢？因为 $y$ 被标记表示 $y$ 到源点的最短路径在之前已经找到，不可能通过别的点再到点 $y$ 从而使 $y$ 到源点源点的距离更短。即：$d[y]$ 已经是最小值了，不可能再小。
4. 循环步骤 2，3直到所有点的最短路径都求出来。

---

.具体示例

\;\;\;\;\;\;\;\;将给出一个具体例子演示如何求最短路。如图：

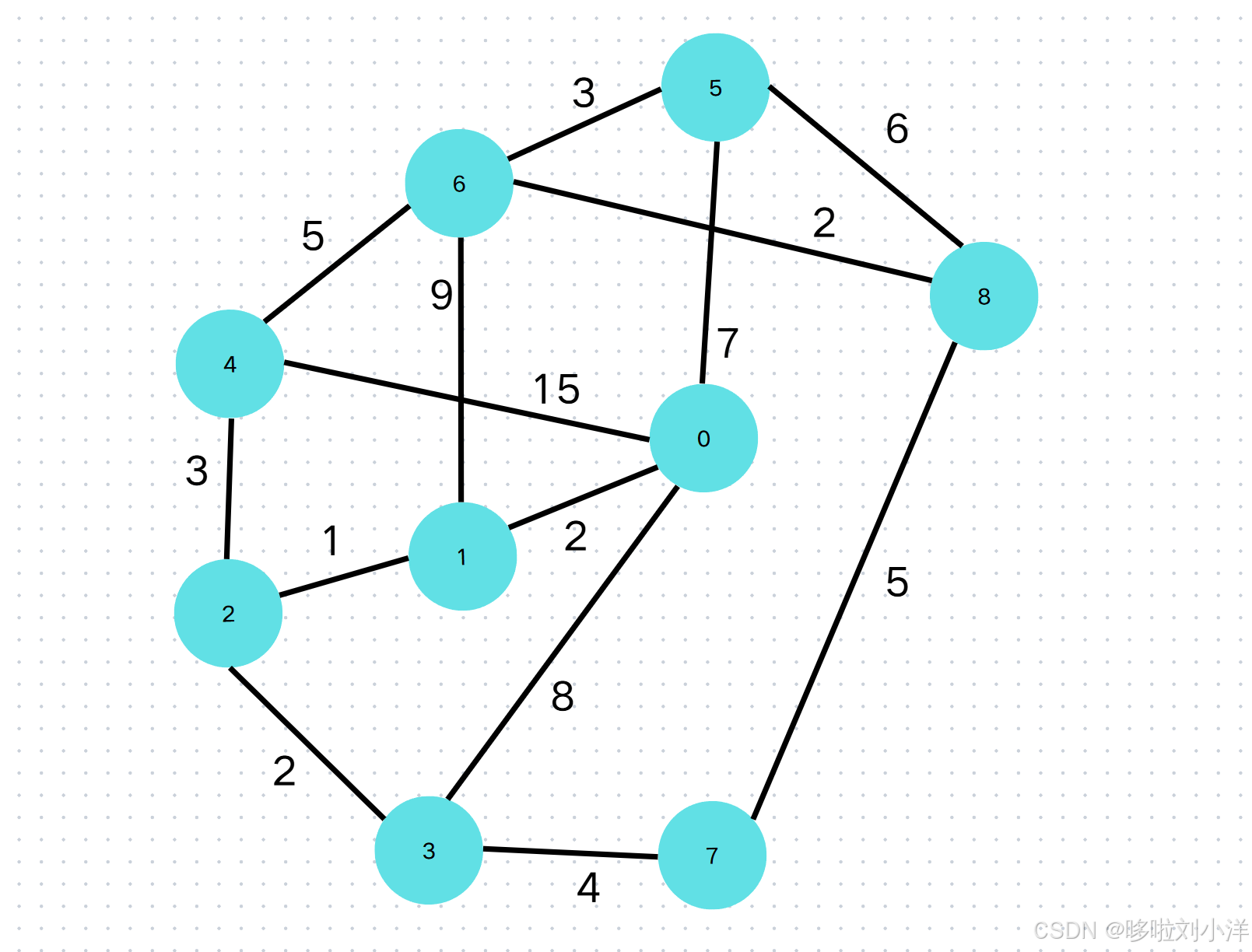
邻接矩阵：
$$\left[\begin{array}{ccccccccc}0& 2& INF& 8& 15& 7& INF& INF& INF\\ 2& 0& 1& INF& INF& INF& 9& INF& INF\\ INF& 1& 0& 2& 3& INF& INF& INF& INF\\ 8& INF& 2& 0& INF& INF& INF& 4& INF\\ 15& INF& 3& INF& 0& INF& 5& INF& INF\\ 7& INF& INF& INF& INF& 0& 3& INF& 6\\ INF& 9& INF& INF& 5& 3& 0& INF& 2\\ INF& INF& INF& 4& INF& INF& INF& 0& 5\\ INF& INF& INF& INF& INF& 6& 2& 5& 0\end{array}\right]$$

QS:求源点（以后都默认为0点）到达其它点的最短路径。

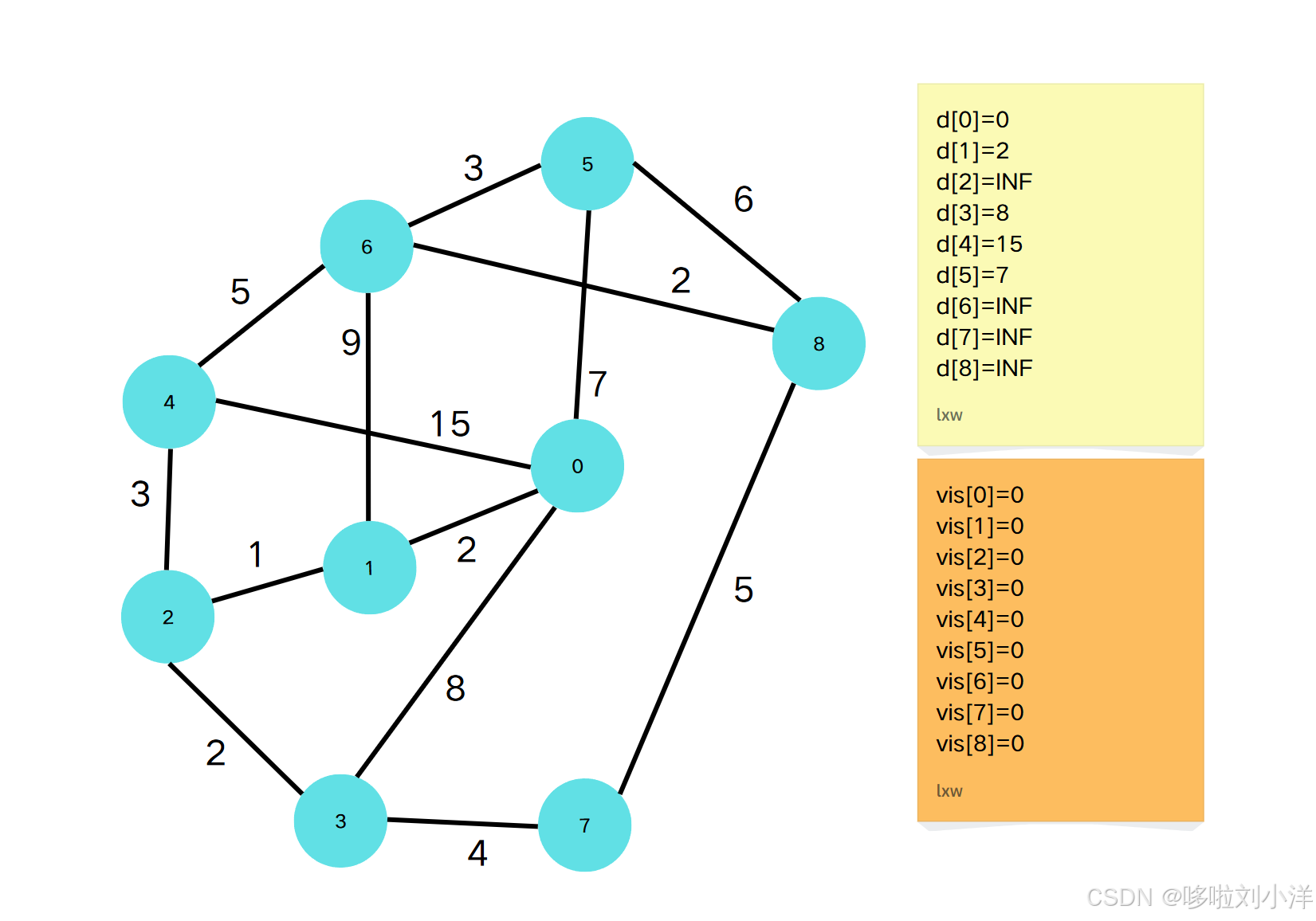
Step1

\;\;\;\;\;\;\;\;初始化数组 $d$ 和数组 $vis$

Step2

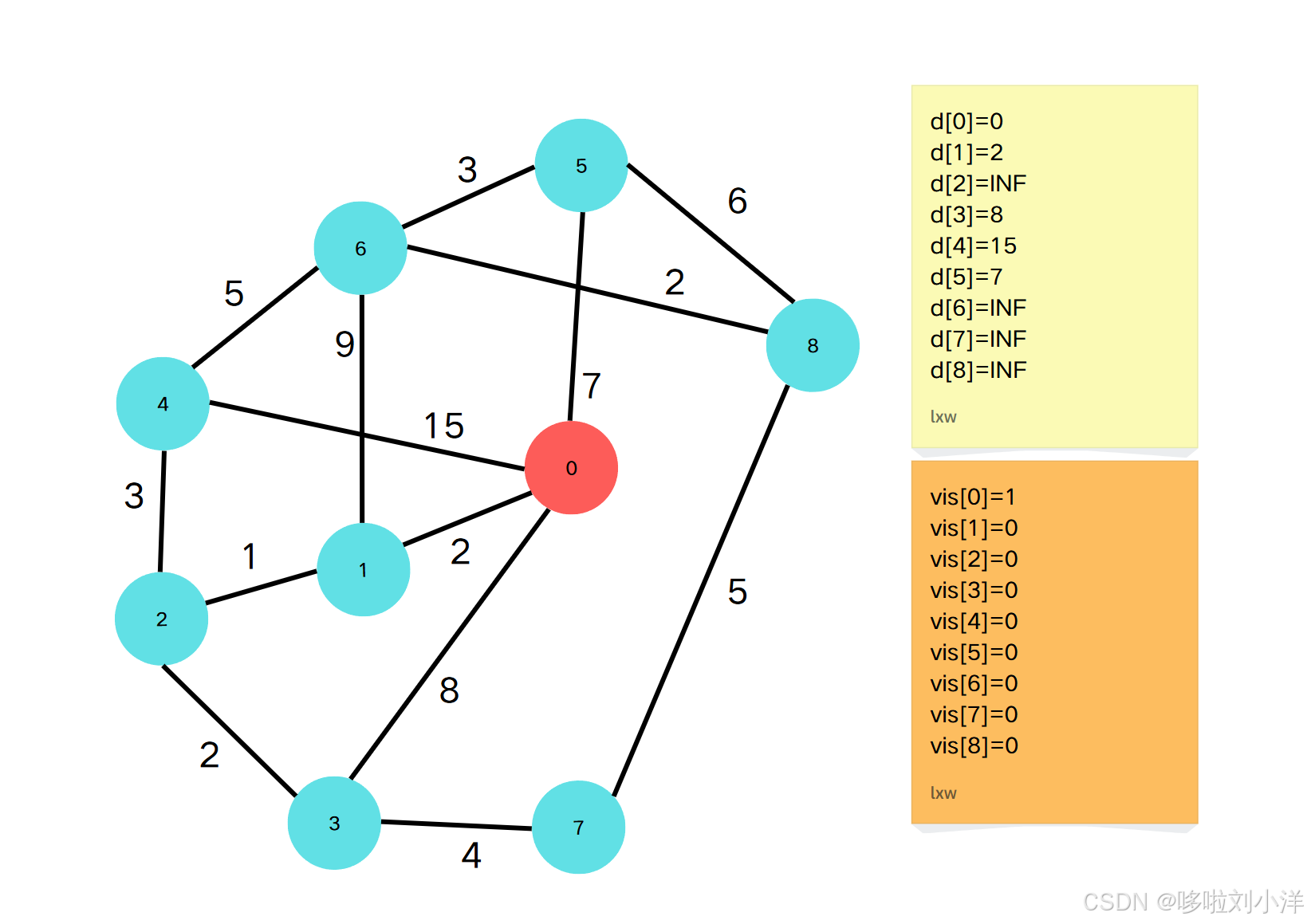
\;\;\;\;\;\;\;\;（强调一遍，$d[i]=j$ 表示当前点 $i$ 到源点的最短距离是 $j$ ）

1. 当前最小的 $d$ 是 $d[0]$ ,因此，$0$ 到源点的最短距离是 $0$，并且将 $vis[0]$ 标记为1。（源点到源点的距离当然是0，这没有什么疑惑。），点0不参与之后的step操作。
2. 因为点0到源点的路径是最短的，那么通过点0去更新0的邻接点{3，4，5}\{3，4，5\}{3，4，5}到源点的距离：
   • $vis[4]=0，d[4]=min(d[4],d[0]+g[0][4])$
   • $vis[5]=0，d[5]=min(d[5],d[0]+g[0][5])$
   • $vis[3]=0，d[3]=min(d[3],d[0]+g[0][3])$
     更新完的图将在下一个步骤中看到d数组的改变

Step3

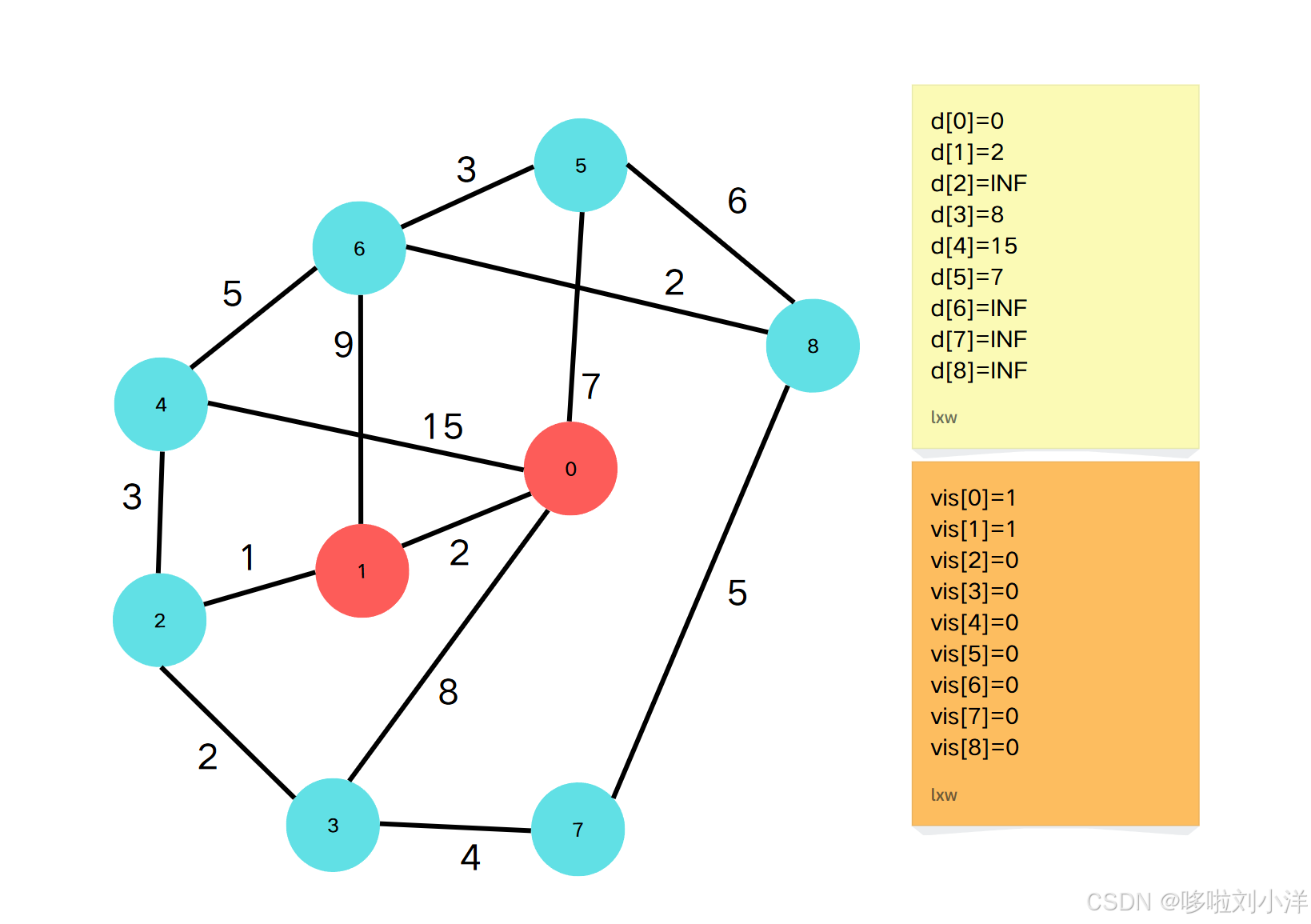
1. 因为$vis[0]=1$, 点0不参与此次最小值比较（后续同理）。所以当前最小的d元素是d[1]=2，因此，点1到源点的最短路径就是2。将vis[1]标记为1.
2. 通过点1更新邻接点{0,2,6}\{0,2,6\}{0,2,6}
   • $vis[0]=1$ , 跳过
   • $vis[2]=0，d[2]=min(d[2],d[1]+g[1][2])$
   • $vis[6]=0，d[6]=min(d[6],d[1]+g[1][6])$

Step4
\;\;\;\;\;

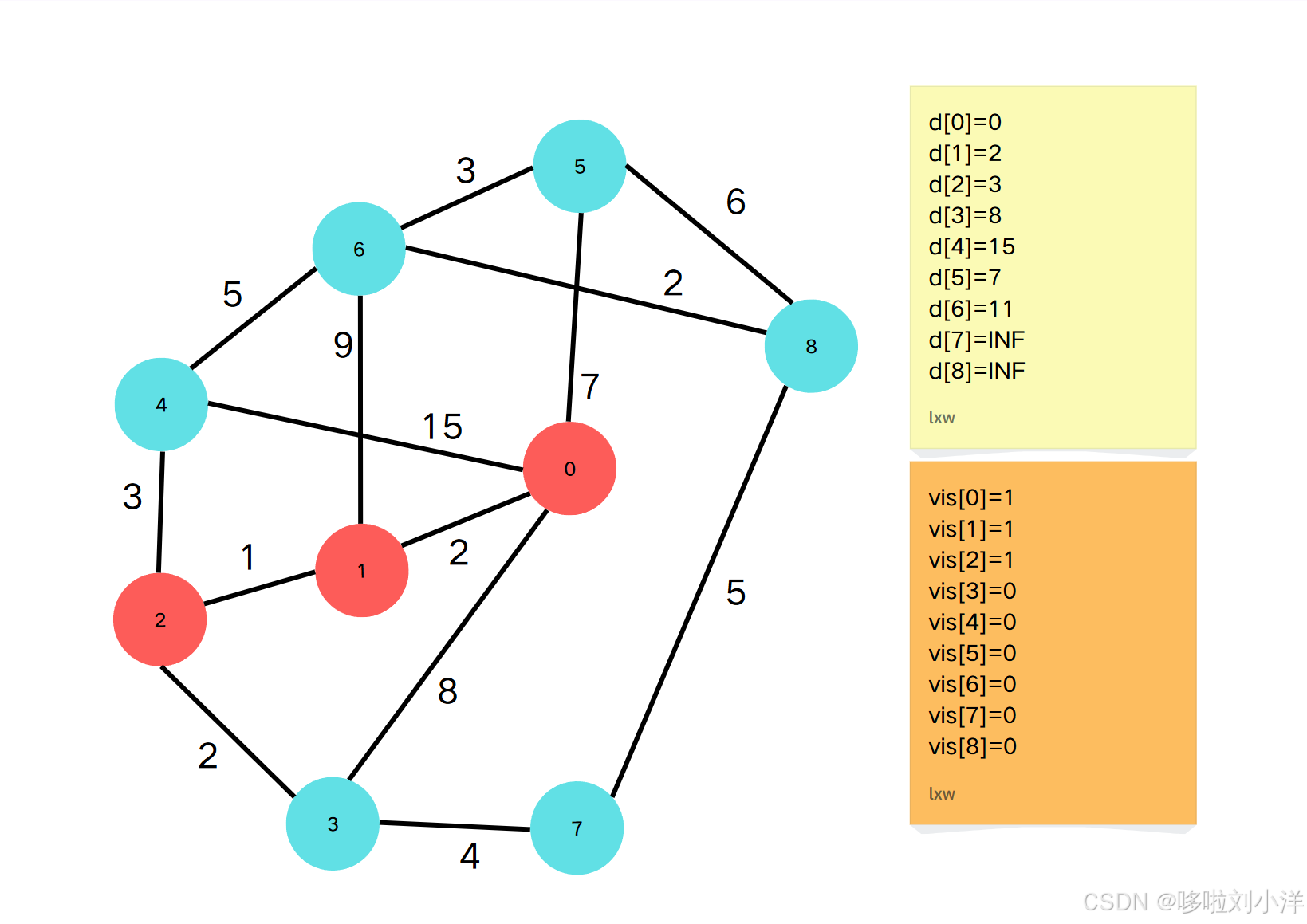
1. 当前 $d$ 最小的 $d$ 元素是 $d[2]=3$ .因此点2到源点的最短路径就是3。并且 $vis[2]$ 标记为 $1$。（注意，上图是上一个步骤操作完且当前步骤标记当前的vis的图，但是没有更新当前步骤的d数组)
2. 通过点2更新邻接点{1,4,3}:\{{1,4,3}\}:{1,4,3}:
   • $vis[1]=1，跳过$
   • $vis[4]=0，d[4]=min(d[4],d[2]+g[2][4])$
   • $vis[3]=0，d[3]=min(d[3],d[2]+g[2][3])$

Step5

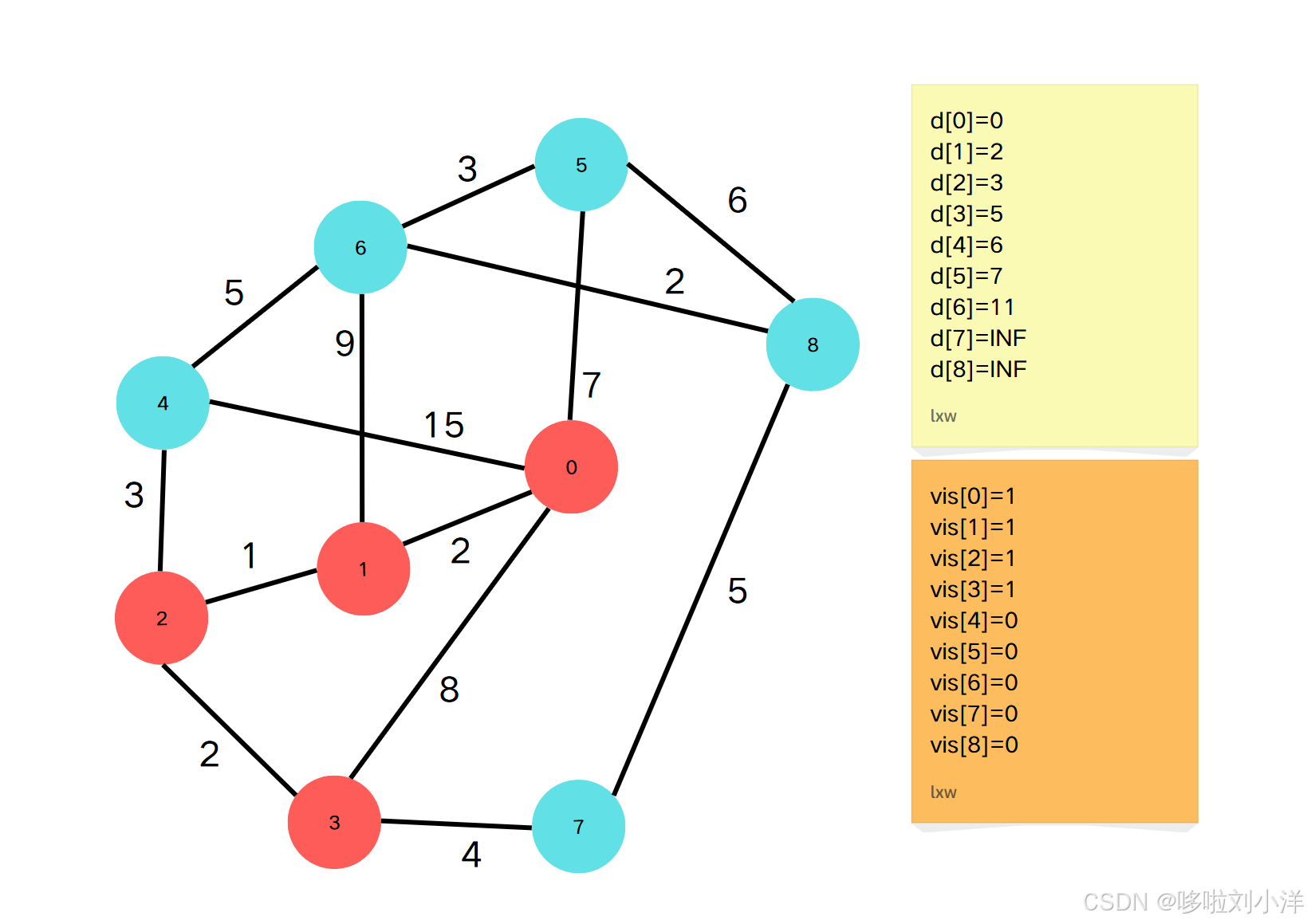
1. 当前 $d$ 最小的 $d$ 元素是 $d[3]=5$ .因此点3到源点的最短路径就是5。并且 $vis[3]$ 标记为 $1$。（注意，上图是上一个步骤操作完且当前步骤标记当前的vis的图，但是没有更新当前步骤的d数组)
2. 通过点3更新邻接点{2,0,7}:\{{2,0,7}\}:{2,0,7}:
   • $vis[2]=1，跳过$
   • $vis[0]=1，跳过$
   • $vis[7]=0，d[7]=min(d[7],d[3]+g[3][7])$

Step6

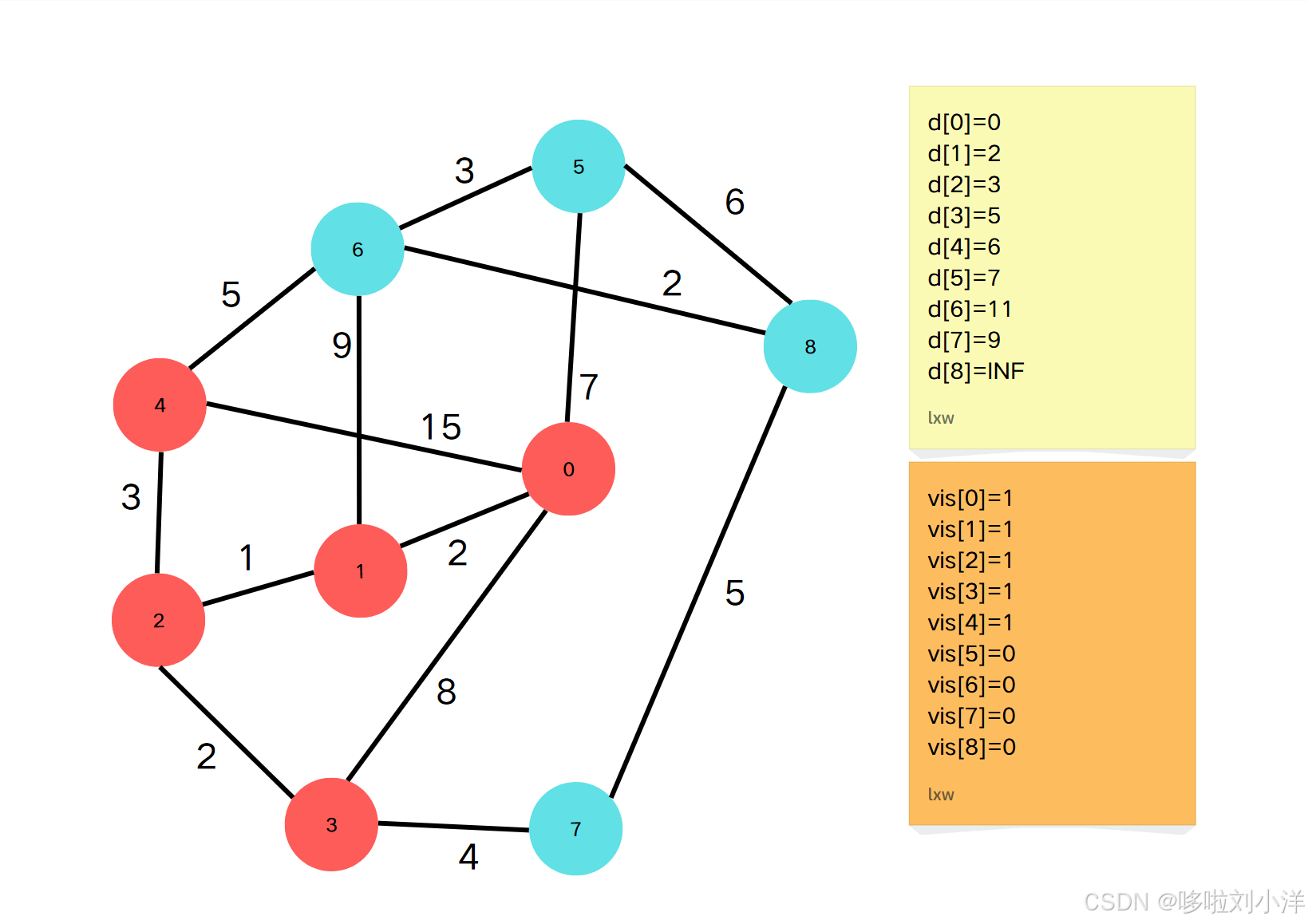
1. 当前 $d$ 最小的 $d$ 元素是 $d[4]=6$ .因此点4到源点的最短路径就是6。并且 $vis[3]$ 标记为 $1$。（注意，上图是上一个步骤操作完且当前步骤标记当前的vis的图，但是没有更新当前步骤的d数组)
2. 通过点4更新邻接点{2,0,6}:\{{2,0,6}\}:{2,0,6}:
   • $vis[2]=1，跳过$
   • $vis[0]=1，跳过$
   • $vis[6]=0，d[6]=min(d[6],d[3]+g[4][6])$

Step7
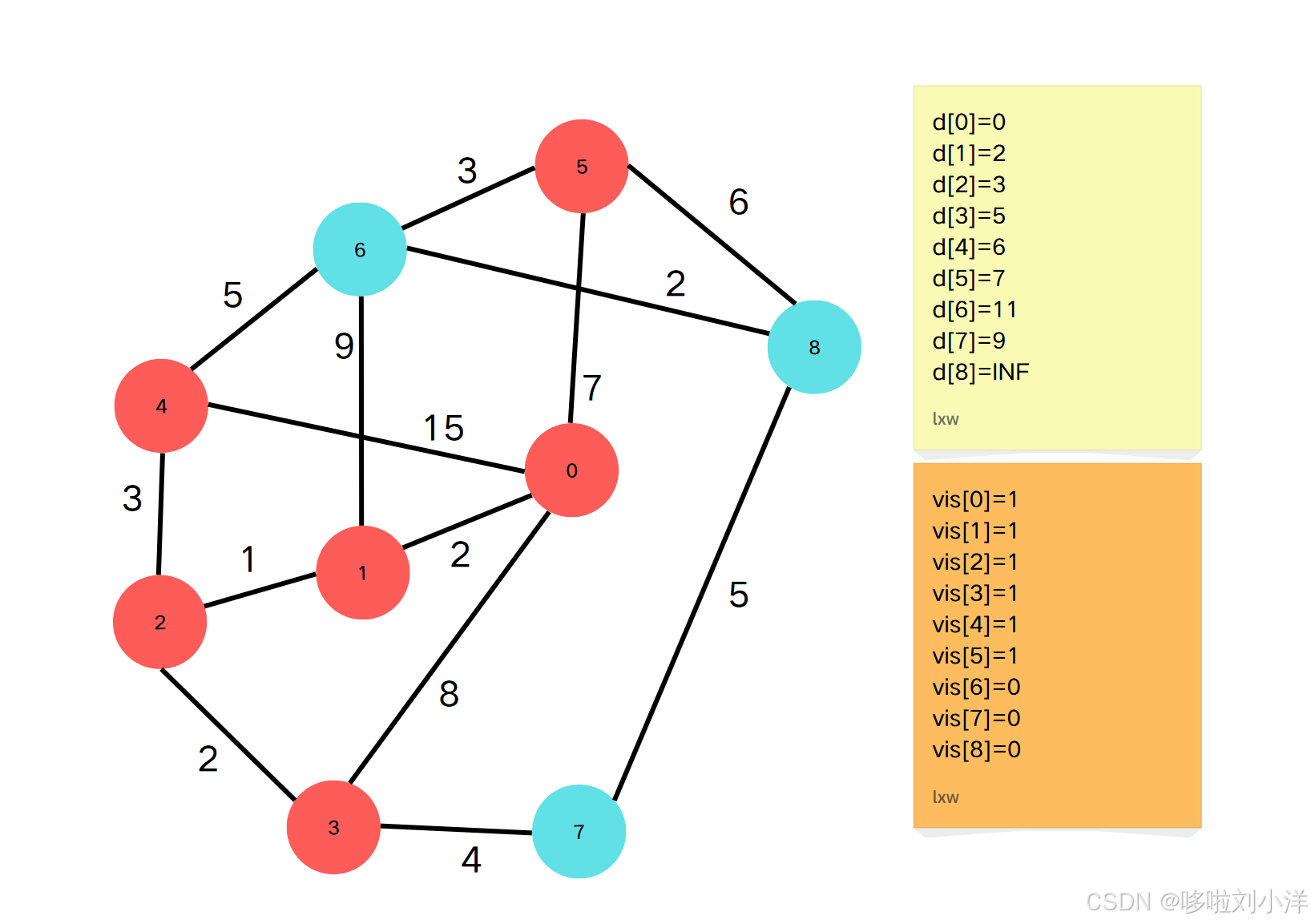1. 当前 $d$ 最小的 $d$ 元素是 $d[5]=7$ .因此点5到源点的最短路径就是7。并且 $vis[5]$ 标记为 $1$。（注意，上图是上一个步骤操作完且当前步骤标记当前的vis的图，但是没有更新当前步骤的d数组)
2. 通过点5更新邻接点{0,6,8}:\{{0,6,8}\}:{0,6,8}:
- $vis[0]=1，跳过$
- $vis[6]=0，d[6]=min(d[6],d[5]+g[5][6])$
- $vis[8]=0，d[8]=min(d[8],d[5]+g[5][8])$

Step8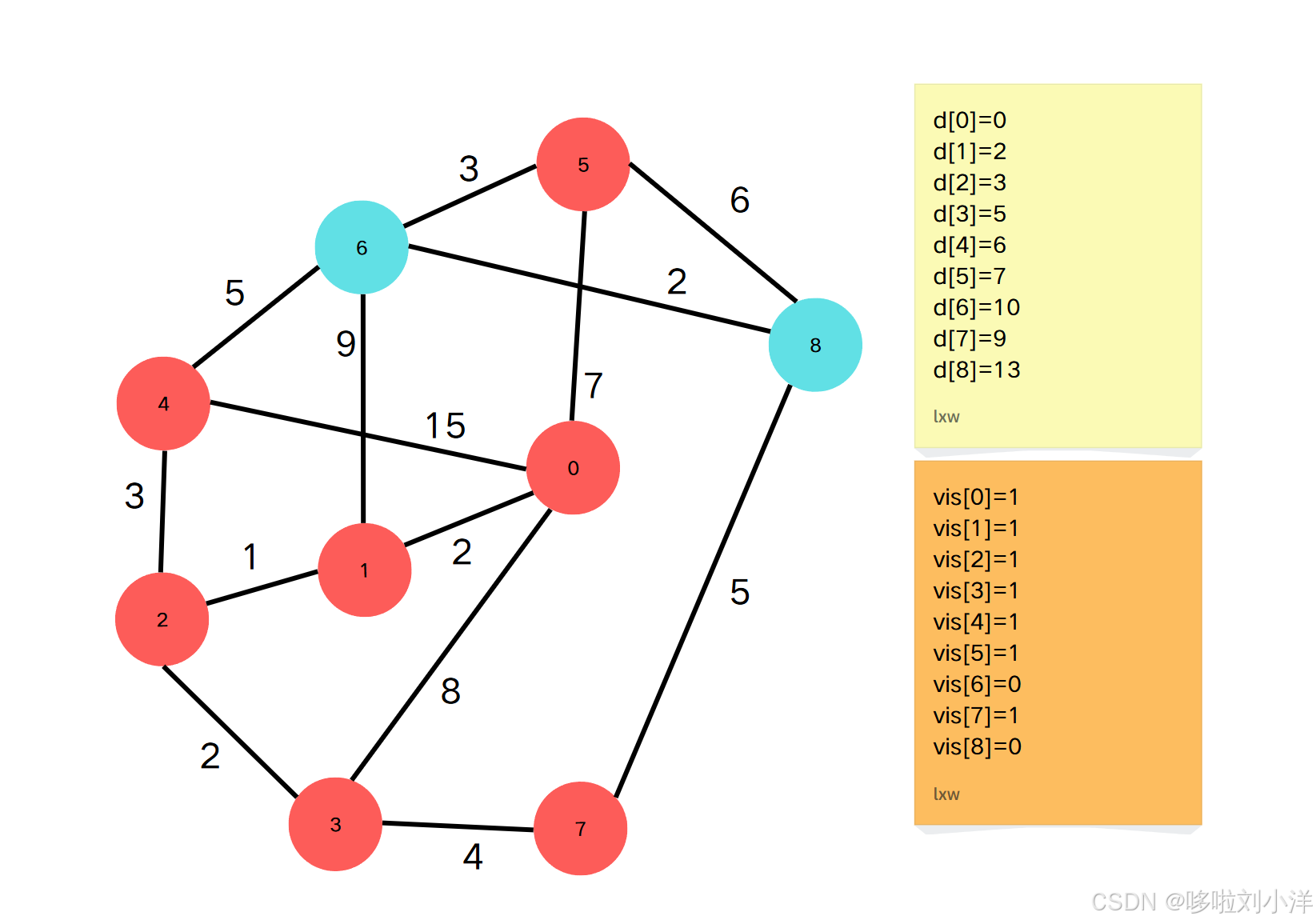

1. 当前 $d$ 最小的 $d$ 元素是 $d[7]=9$ .因此点7到源点的最短路径就是9。并且 $vis[7]$ 标记为 $1$。（注意，上图是上一个步骤操作完且当前步骤标记当前的vis的图，但是没有更新当前步骤的d数组)
2. 通过点7更新邻接点{3,8}:\{{3,8}\}:{3,8}:
   • $vis[3]=1，跳过$
   • $vis[8]=0，d[8]=min(d[8],d[5]+g[5][8])$

Step9

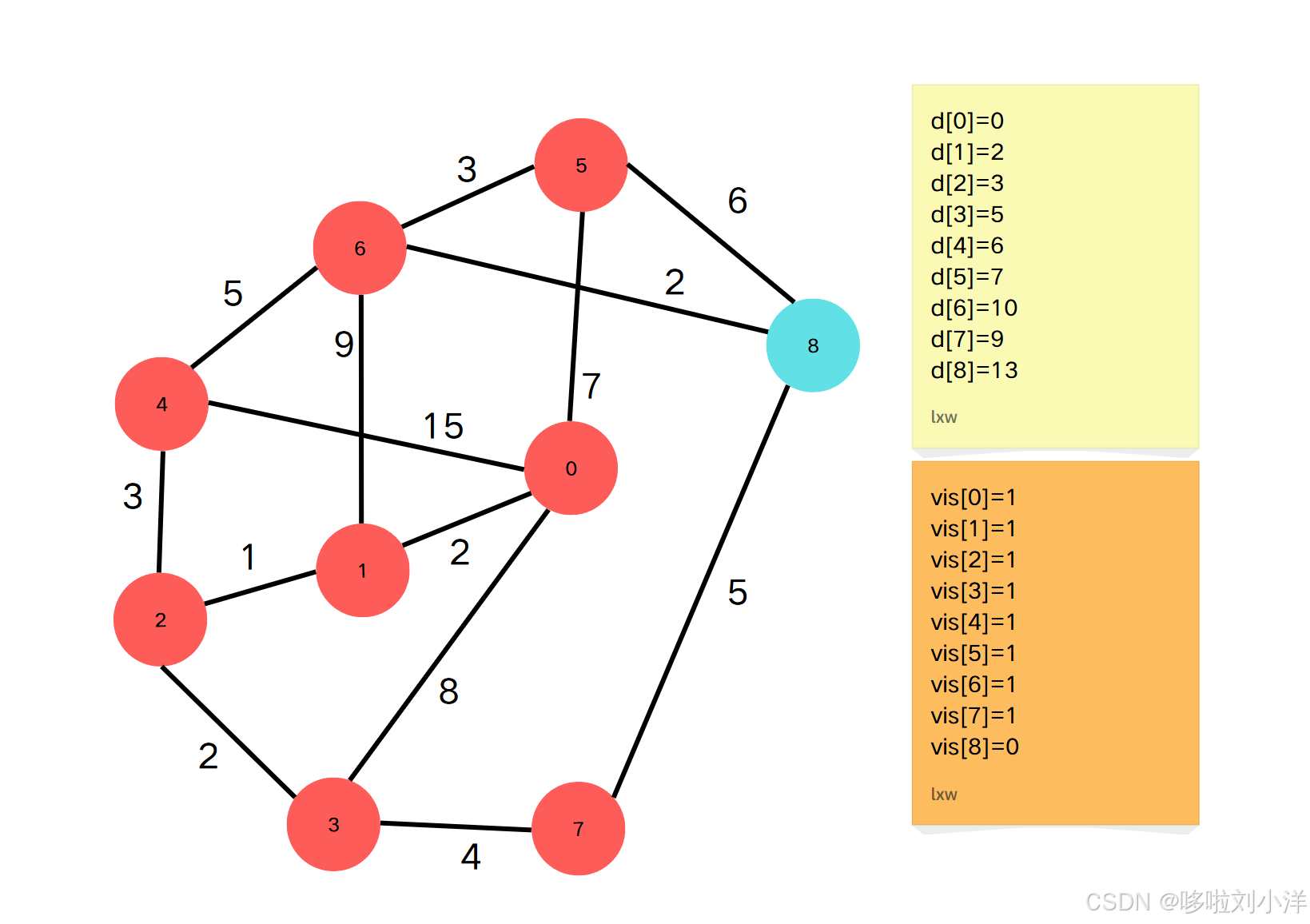
1. 当前 $d$ 最小的 $d$ 元素是 $d[6]=10$ .因此点6到源点的最短路径就是10。并且 $vis[6]$ 标记为 $1$。（注意，上图是上一个步骤操作完且当前步骤标记当前的vis的图，但是没有更新当前步骤的d数组)
2. 通过点6更新邻接点{4,5,8}:\{{4,5,8}\}:{4,5,8}:
   • $vis[4]=1，跳过$
   • $vis[5]=1，跳过$
   • $vis[8]=0，d[8]=min(d[8],d[5]+g[6][8])$

Step10

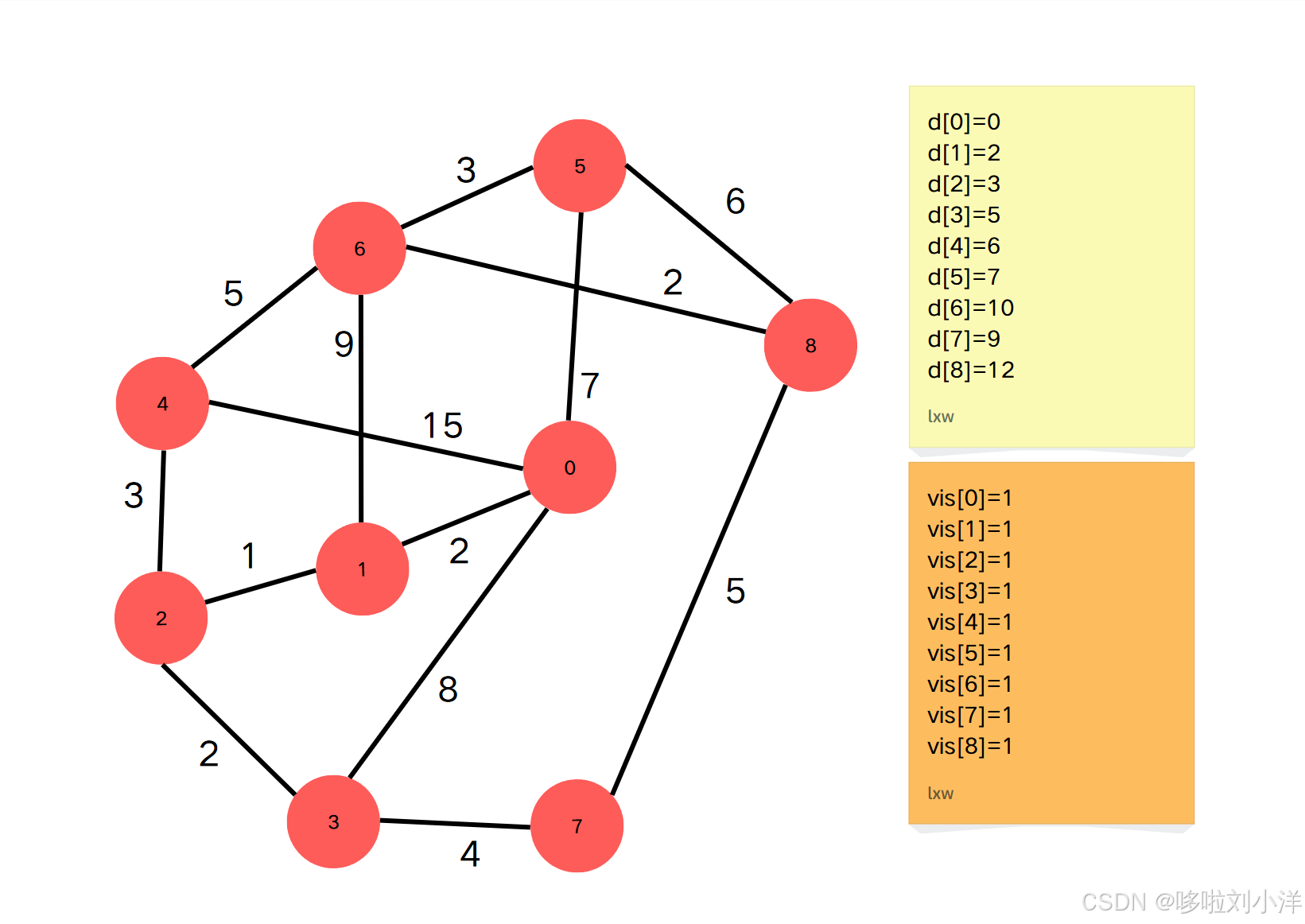
1. 当前 $d$ 最小的 $d$ 元素是 $d[8]=12$ .因此点8到源点的最短路径就是12。并且 $vis[8]$ 标记为 $1$。（注意，上图是上一个步骤操作完且当前步骤标记当前的vis的图，但是没有更新当前步骤的d数组)

2. 通过点8更新邻接点{5,6,7}:\{{5,6,7}\}:{5,6,7}:

   • $vis[5]=1，跳过$
   • $vis[6]=1，跳过$
   • $vis[7]=1，跳过$

到此，所有点到源点（点0）的最短路径全部求出来了。这里引出的问题是，对于每个步骤最小的 $d[i]$ ,为什么这个 $d[i]$ 就是点 $i$ 到源点的最短路径，会不会有更短的路径比当前的 $d[i]$ 更小？

---

---

.贪心证明

\;\;\;\;\;\;\;接着上面引出的问题，来解释DJ算法最重要的一步，贪心的正确性！

对于点0，起到源点的距离是0，也就是0，这个看似没有什么疑惑的地方。✅

此时已经找到了最短路径的点集合是 {0}\{0\}{0} ,没有找到最短路径点的集合是{1,2,3,4,5,6,7,8}\{1,2,3,4,5,6,7,8\}{1,2,3,4,5,6,7,8}，此时 $d[1]=2$ 最小，那么可以肯定，点1到源点的最短路径就是2。

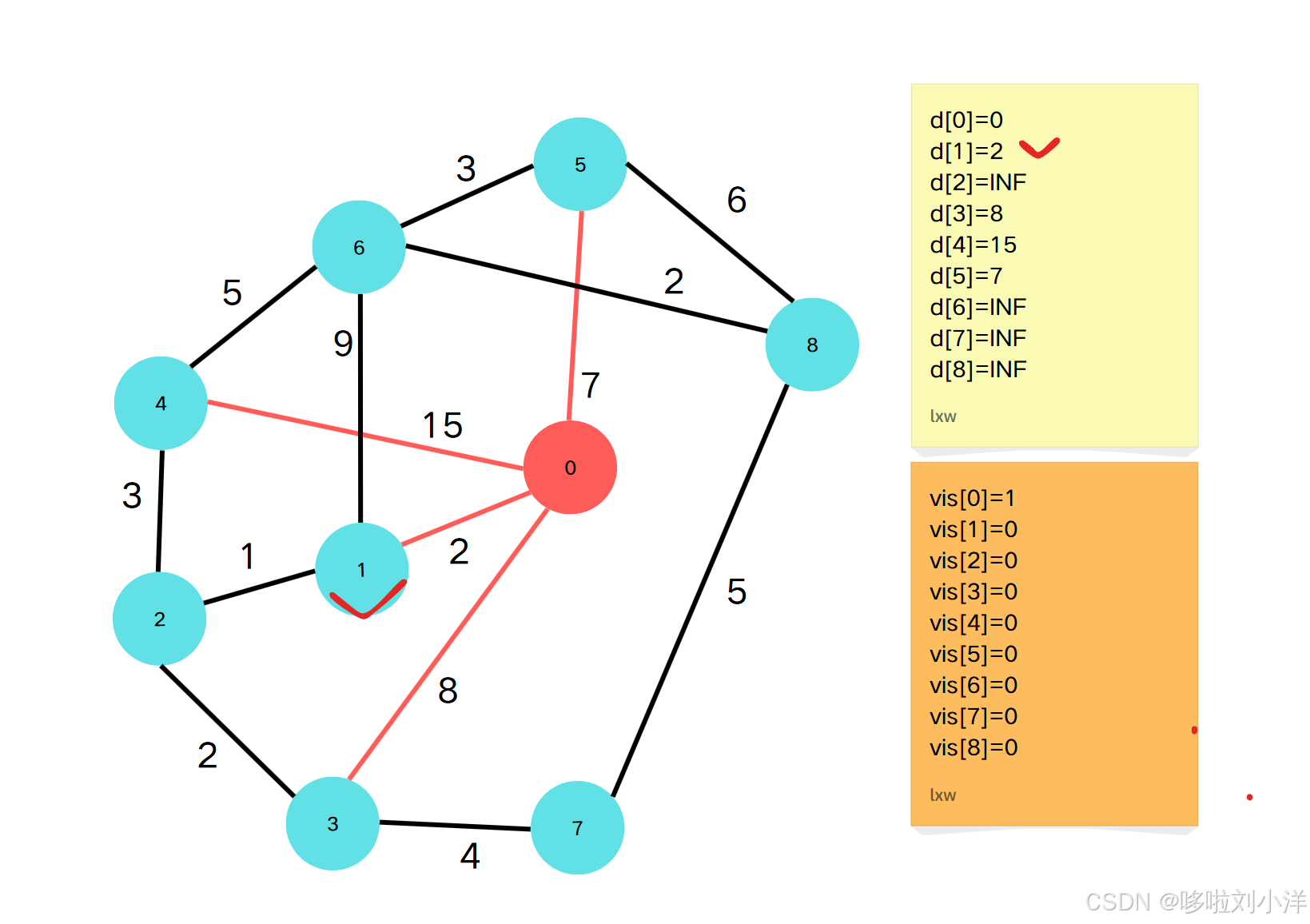
反证法：
假设当前点1到源点的最短路径不是2，即不是"1-0"这条路径。

那么也就是说，至少有一条其它路径到点1的距离比2更小。但是这是不可能的，因为此时到达源点的所有点中，“1-0”已经是最短的，其余所有的点到源点的距离都大于等于2，如图：“4-0”，“5-0”，“3-0”。在这三条大于“1-0”的边，再加上一条边或者若干条边最后到达点1，绝对不可能比“1-0”小。

一叶知秋，其余的点也同理。
在当前已知的路径中，找到距离源点最短的点x，那么这个点x到源点的路径是最短路径。因为不可能从第二短的点通过后续更新操作找到一条路径到达x比当前更短。首先，第二短的路径本身就比x到源点长了，再加上若干边，更不会小于当前x到源点的距离。

更新操作也是必要的，更新操作也叫做松弛操作，即从当前最短路径的点出发，去更新和x的邻接点，这很好理解。因为d[x]最小，比如有d[y]比d[x]大一点，但是d[x]+g[x][y]可能小于d[y]，如此，y距离源点最短路径就被d[x]更新。更新操作时保证每次选择最小的d元素的前提。换句话说，更新操作是DJ算法贪心的前提。

.代码分段解释

1.初始化

#include<iostream>
using namespace std;
const int N=10010;
const int INF = 0x3f3f3f3f;  // 无穷大int d[N];    //d[i]=j表示i距离源点最短路径是j
bool vis[N];   //vis[i]=true 表示i点已经找到最短路径
int g[N][N];   //g[i][j]=x表示点i到点j的距离是xvoid init()
{g[9][9] = {{0, 2, INF, 8, 15, 7, INF, INF, INF},{2, 0, 1, INF, INF, INF, 9, INF, INF},{INF, 1, 0, 2, 3, INF, INF, INF, INF},{8, INF, 2, 0, INF, INF, INF, 4, INF},{15, INF, 3, INF, 0, INF, 5, INF, INF},{7, INF, INF, INF, INF, 0, 3, INF, 6},{INF, 9, INF, INF, 5, 3, 0, INF, 2},{INF, INF, INF, 4, INF, INF, INF, 0, 5},{INF, INF, INF, INF, INF, 6, 2, 5, 0}};memset(vis,false,sizeof vis);memset(d,0x3f3f3f3f,sizeof d);
}

2.DJ执行

void DJ(int n)
{d[0]=0;vis[0]=true;for(int i=0;i<n;i++)  //每次循环找到一个点到源点的最短路径{int k=-1;for(int j=0;j<n;j++)   //贪心找到当前最短路径k{if(!vis[j]&&(k==-1||d[i]<d[k])){k=j;}}vis[k]=true;//更新操作for(int j=0;j<n;j++){if(!vis[j]){d[j]=min(d[j],d[k]+g[k][j]);}}}
}

---

.代码汇总

#include<iostream>
using namespace std;const int INF = 0x3f3f3f3f;  // 无穷大int d[10];    //d[i]=j表示i距离源点最短路径是j
bool vis[10];   //vis[i]=true 表示i点已经找到最短路径
int g[10][10];   //g[i][j]=x表示点i到点j的距离是xint n=9;;void init()
{g[9][9] = {{0, 2, INF, 8, 15, 7, INF, INF, INF},{2, 0, 1, INF, INF, INF, 9, INF, INF},{INF, 1, 0, 2, 3, INF, INF, INF, INF},{8, INF, 2, 0, INF, INF, INF, 4, INF},{15, INF, 3, INF, 0, INF, 5, INF, INF},{7, INF, INF, INF, INF, 0, 3, INF, 6},{INF, 9, INF, INF, 5, 3, 0, INF, 2},{INF, INF, INF, 4, INF, INF, INF, 0, 5},{INF, INF, INF, INF, INF, 6, 2, 5, 0}};memset(vis,false,sizeof vis);memset(d,0x3f3f3f3f,sizeof d);
}void DJ(int n)
{d[0]=0;vis[0]=true;for(int i=0;i<n;i++)  //每次循环找到一个点到源点的最短路径{int k=-1;for(int j=0;j<n;j++)   //贪心找到当前最短路径k{if(!vis[j]&&(k==-1||d[i]<d[k])){k=j;}}vis[k]=true;//更新操作for(int j=0;j<n;j++){if(!vis[j]){d[j]=min(d[j],d[k]+g[k][j]);}}}
}void test()
{DJ();for(int i=0;i<n;i++)cout<<d[i]<<" ";return;
}int main()
{test();return 0;
}

.进阶版本代码

\;\;\;\;\;\;\;\;DJ算法有一个优化的版本。即堆优化版。我们发现，在寻找最小的 $d$ 数组元素的时候，时间复杂度是 $O(n)$。这里可以用一个小根堆来存储d数组。这样插入，删除元素的时间复杂度是$O(logn)$。

#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;const int MAXN = 1005;  // 最大节点数
const int INF = 0x3f3f3f3f;int n, m;  // 节点数、边数
int g[MAXN][MAXN];  // 邻接矩阵
int d[MAXN];  // 源点到各节点的最短距离
bool vis[MAXN];  // 标记节点是否已确定最短路径// 优先队列中的元素：(距离, 节点)，小根堆（默认按距离升序）
using PII = pair<int, int>;void dijkstra(int start) {// 初始化距离数组memset(d, 0x3f, sizeof(d));d[start] = 0;memset(vis, false, sizeof(vis));// 小根堆，存储待处理的节点（距离, 节点）priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, start});  // 起点入堆while (!heap.empty()) {// 1. 取出当前距离源点最近的节点auto [dist, u] = heap.top();heap.pop();// 如果节点已确定最短路径，直接跳过if (vis[u]) continue;vis[u] = true;// 2. 用u更新所有未确定的节点v的距离for (int v = 0; v < n; v++) {if (d[v] > d[u] + g[u][v]) {d[v] = d[u] + g[u][v];heap.push({d[v], v});  // 新距离入堆}}}
}int main() 
{// 示例：初始化图（节点0~n-1）cin >> n >> m;memset(g, 0x3f, sizeof(g));for (int i = 0; i < n; i++) {g[i][i] = 0;  // 自身到自身距离为0}// 读入边for (int i = 0; i < m; i++) {int u, v, w;cin >> u >> v >> w;g[u][v] = min(g[u][v], w);  // 处理重边，保留最小权值}// 计算从源点0出发的最短路径dijkstra(0);// 输出结果for (int i = 0; i < n; i++) {if (d[i] == INF) {cout << "INF ";  // 不可达} else {cout << d[i] << " ";}}return 0;
}

.leetcode习题

.743