浅谈背包DP（C++实现，配合lc经典习题讲解）

        很久没有更新数据结构与算法的专题文章了，也很久没有好好刷算法题了，很惭愧。之前我们介绍过由递归到记忆化搜索再到动态规划的演进过程，从本文开始我们将见识一些常见的动态规划题目模型，在互联网大厂笔试面试出现的概率极高！今天我们来介绍“背包DP”这一模型，并结合leetcode的经典题目来进行真题讲解。常见的背包DP的类型有"0/1背包"，“完全背包”，“分组背包”这三种，我们会依次结合场景对其进行介绍！此处声明，我的文章是我学习左程云老师算法课程的笔记回顾。

一.0/1背包

        首先我们来看一个场景：

        给定一个正数t，表示背包容量，有m个货物，每个货物只能选一次。每个货物都有自己的体积cost[i]和价值value[i]，返回在不超过总容量的情况下，最大的价值。

        朋友们可以很明显的看到，我把“只能选一次”这个关键的字眼给标红了！没错，这就是区分不同背包DP的关键所在。任何背包问题的尝试思路就在于“要么选，要么不选”！但是区别在于“怎么选，选几个”。在这个场景中，我们要解决的问题是：在 背包容量 t 的限制下，选择若干件物品（每件物品最多选一次），使得 总价值最大。接下来最重要的就是我们该如何拆解并且整理出来这个尝试模型，而一个很关键的点在于我们需要找出这个场景中的可变参数。

        之前我们有介绍过，在动态规划问题中，状态设计的核心思想是用最少的参数，描述“一个子问题的局面”，那么关键就是我们如何把这个大问题拆解成若干子问题。本题目的“子问题”至少需要两个维度的参数来进行刻画。首先是货物的范围i：如果我们考虑“前i个货物”，就能把这个大问题逐步拆分，这是典型的分治思路。其次是背包容量上限j：当容量限制是j时，能装下的货物肯定和容量为j-1时不同，即容量限制会影响选择结果，所以剩余容量大小也必须是一个考虑维度。由此我们定义dp[i][j]为只考虑前i个物品，并且容量不超过j的情况下，能获得的最大价值。显然，dp[m][t]就是我们要求得的答案。

        现在dp[i][j]的含义已经确定，那么我们接下来首先讨论边界情况，再整理状态转移方程。当i==0时，也就是说根本不存在货物，那么哪来的价值一说呢？所以dp[0][j]==0。当j==0时，无论有多少货物都装不下任何一个，所以dp[i][0]==0。接下来讨论一般情况，此时我们面对第i个货物(体积cost[i]，价值value[i])有两种选择。首先我们可以不选第i件货物，这样价值就是dp[i-1][j](实际上沿用了面对第i-1个货物时的选择结果)。如果我们选第i件货物，这里有一个前提，就是j>=cost[i]，这就意味着我们决定在容量j中消费cost[i]，来获取value[i]，此时价值就是dp[i-1][j-cost[i]]+value[i]，我们只需在这些可能情况中取最大值即可。我们可以整理出如下的状态转移方程：

dp[i][j]=max(dp[i-1][j],dp[i-1][j-cost[i]]+value[i]) (j>=cost[i])

dp[i][j]=dp[i-1][j] (j<cost[i])

由此我们可以画出如下的动态规划表：

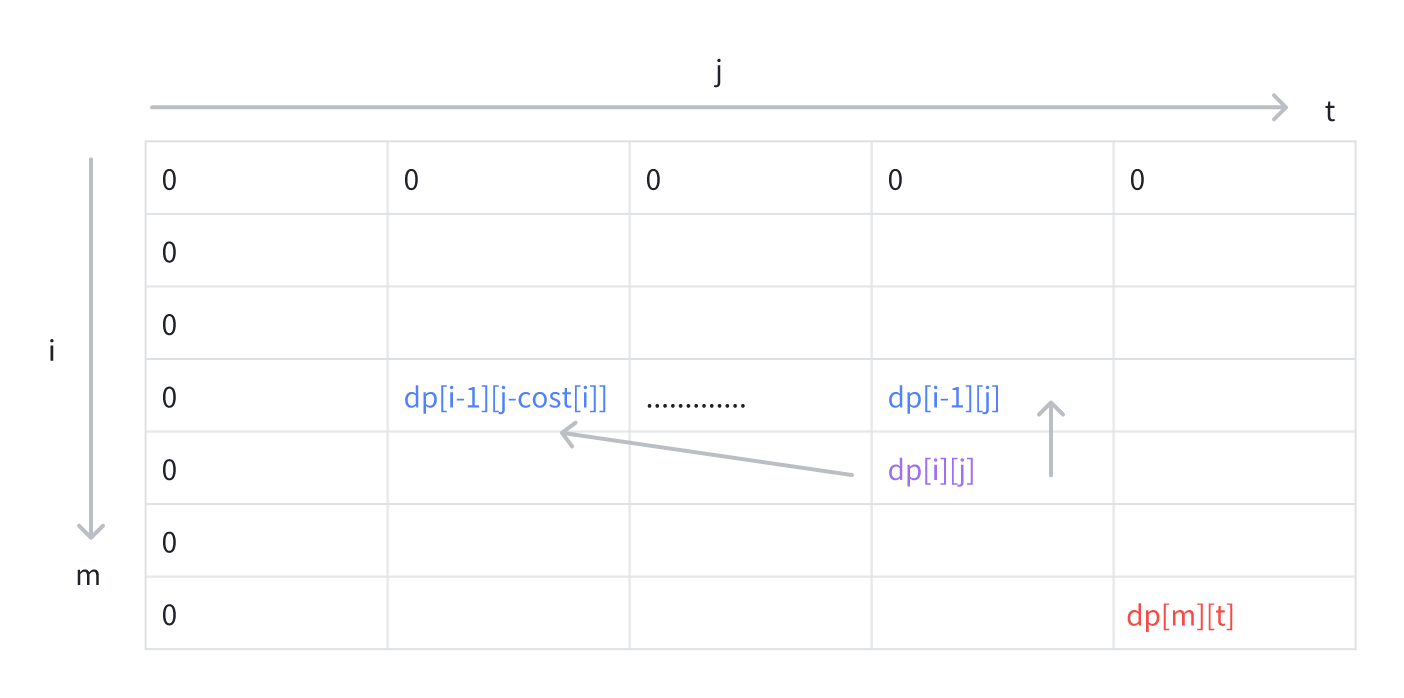
根据状态转移方程和动态规划表可以总结出下面的模板代码：

class solution{
public:int zero_onebackpack(vector<int>&cost,vector<int>&value,int m,int t){vector<vector<int>> dp(m+1,vector<int>(t+1,0));for(int i=1;i<=m;i++){for(int j=1;j<=t;j++){if(j-cost[i]<0){dp[i][j]=dp[i-1][j];}else{dp[i][j]=max(dp[i-1][j],dp[i-1][j-cost[i]]+value[i]);}}}return dp[m][t];}
};

        相信朋友们已经对0/1背包的场景和解题思路有了一定的认知，我们通过下面两道比较经典的题目来巩固一下~

leetcode 464 分割等和子集

        理解题意后，我们对这道题目进行分析。这道题给人的感觉乍看可能是用前缀和或者双指针类的数组技巧解，惭愧来说，我几个月前第一次做这道题也完全没往动态规划的方向想，绕了很大一圈。我们可以转换一下题意：题目是让我们判断一个数组能不能分成两个等和的子集，可以转换为能否从数组里选出若干数字（货物），使得它们的和正好等于数组元素总和的一半（背包容量）？这样这道题目就转换为了一个经典的0/1背包问题，因为每个数只能取一次！和传统的模板题区别在于，其要求选取的“货物体积”总和要正好等于“背包容量”。除此之外我认为这道题目还需要注意的就是建边，就是这个数组的和必须为偶数，由于是整数数组，不可能将其划分为两个等和子集。其余讨论细节与上面的模板题几乎一致，此处不再赘述，示例代码如下：

class Solution {
public:bool canPartition(vector<int>& nums) {int n = nums.size();if (n < 2) return false;int sum = accumulate(nums.begin(), nums.end(), 0);if (sum & 1) return false;int target = sum / 2;int maxNum = *max_element(nums.begin(), nums.end());if (maxNum > target) return false;vector<vector<bool>> dp(n + 1, vector<bool>(target + 1, false));dp[0][0] = true;for (int i = 1; i <= n; i++) {for (int j = 0; j <= target; j++) {if (j < nums[i - 1]) {dp[i][j] = dp[i - 1][j]; } else {dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];}}}return dp[n][target];}
};

leetcode 494 目标和

        这是一道非常妙的0/1背包模型转换问题，据我所知也很高频次的出现在大厂的笔试面试场上进行手撕。和leetcode 1049 最后一块石头的重量II的转化过程有异曲同工之妙，我们需要触类旁通，举一反三。首先我们来看数据量，只有20，那么通过DFS暴搜大概率是能过的。如果要通过记忆化搜索剪枝也没问题，不过需要注意因为key可能为负，我们不能简单粗暴的利用数组做缓存，而是用哈希表做。由此可以整理出严格位置依赖的动态规划表进行求解，这一套我们之前的文章有系统的介绍过这个方法论，此处不加赘述。我们来思考下面几个问题，首先，对于数组nums来说，是否有负数其实并不影响结果！因为正负是可以通过+，-来颠倒的。其次，当目标和大于数组累加和时，完全不可能有这种方案；无论如何加减，都不会影响最终结果的奇偶性，如果和目标和奇偶性不符，这两种情况直接返回0，这是小剪枝。最关键的点来了，我们通过下图来推演一下：

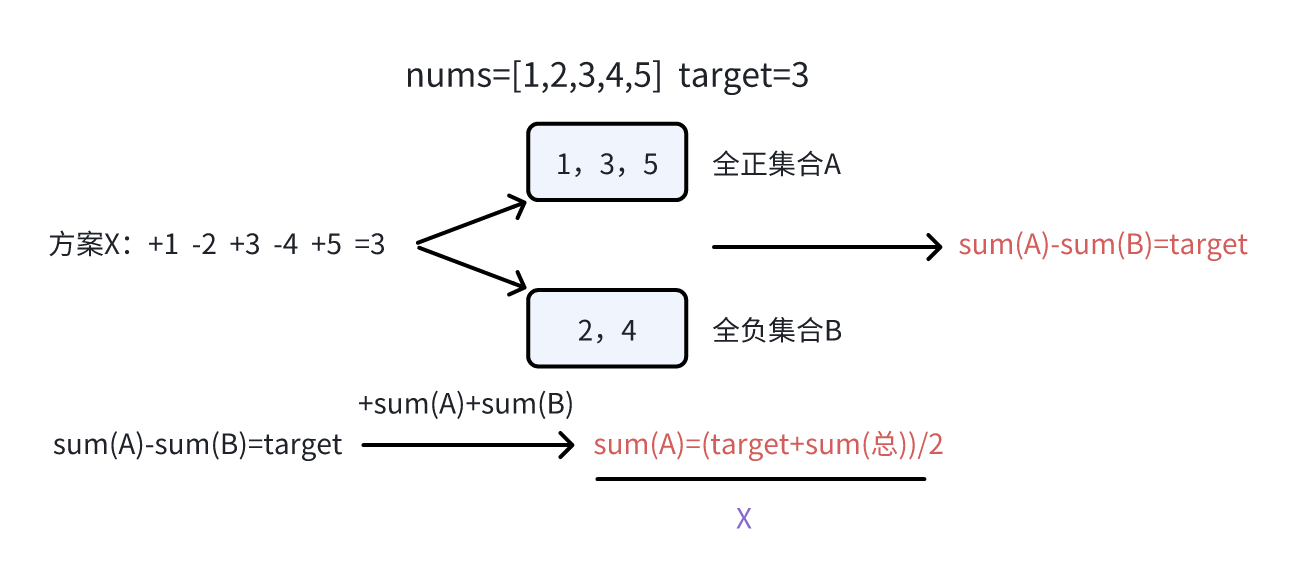
        这其实本质上是个数学层面的变形了。拿上图举例，我们抽选出其中一组用例进行分析，我们把数组中的数依照正负划分为两个集合，依据题设，目标和应该等于两个集合累加和的差值。这里的变换很有意思，等式两边同时加上两个集合的累加和，我们把(target+sum(总))/2这个整体抽象为一个新目标值X，那么这个问题就转化为：在数组nums中，有多少种子集合累加和刚好等于X的方案数！这妥妥是个0/1背包问题。dp[i][j]表示前i个数字构成的累加和为j的子序列数量。接下来的分析过程就与传统的0/1背包问题，具体过程不再赘述，示例代码如下：

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum=0;for(int num:nums){sum+=num;}if(abs(target)>sum||((target+sum)&1)){return 0;}int x=(target+sum)/2;int n=nums.size();vector<vector<int>> dp(n+1,vector<int>(x+1,0));dp[0][0]=1;for(int i=1;i<=n;i++){int num=nums[i-1];for(int j=0;j<=x;j++){dp[i][j]=dp[i-1][j];if(j>=num){dp[i][j]+=dp[i-1][j-num];}}}return dp[n][x];}
};

二.完全背包

        完全背包和前面0/1背包的场景实际上大体相同。唯一不同的点在于每个货物可以取无限次。对于完全背包问题而言，dp[i][j]的含义仍然是只考虑前i个物品，并且容量不超过j的情况下，能获得的最大价值。且最终求得的结果仍是dp[m][t]，理由和0/1背包完全一样，此处不加赘述。我们的尝试思路仍然建立在“要么选，要么不选”的基础上。我们面对第i个货物时，我们可以不选，这样价值还是dp[i-1][j]。关键在于如果我们选，由于我们可以选无限次，只需要保证背包容量有空余就行。但是我们选了之后，可考虑的范围就不再是之前的[0~i-1]了，因为i位置的货物还能重复选！所以此时的价值是dp[i][j-cost[i]]+value[i]。我们只需在这些可能情况中取最大值即可。我们可以整理出如下的状态转移方程：

dp[i][j]=max(dp[i-1][j],dp[i][j-cost[i]]+value[i]) (j>=cost[i])

dp[i][j]=dp[i-1][j] (j<cost[i])

根据状态转移方程可以总结出下面的模板代码（leetcode 322零钱兑换就是模板题）：

class solution{
public:int complete_backpack(vector<int>&cost,vector<int>&value,int m,int t){vector<vector<int>> dp(m+1,vector<int>(t+1,0));for(int i=0;i<m;i++){for(int j=0;j<t;j++){if(j-cost[i]<0){dp[i][j]=dp[i-1][j];}else{dp[i][j]=max(dp[i-1][j],dp[i][j-cost[i]]+value[i]);}}}return dp[m][t];}
};

        相信朋友们已经对完全背包的场景和解题思路有了一定的认知，我们通过下面两道比较经典的题目来巩固一下~

leetcode 279 完全平方数

        理解题意后我们来分析这道题目：我们把“平方和数组”抽象成“一堆货物”，而这个参数n可以表示“背包的容量上限”。我个人认为这道题还是比较容易联想到背包模型的。但是与前面的题目不一样，这里面同一个完全平方数可以无限次取，只要总和不超过n即可，这就是一个背包容量为n的完全背包问题，dp[i][j]的含义是前i个平方数拼出数字j所需的最少数量。实际上，任何一个数n都可以由n个1构成，但是这没有意义，所以题设是求最少的完全平方数的数量。我们只需要构造出一个平方数数组，类比成模板的cost数组，其余逻辑包括建边几乎和模板题没有任何出入，此处不再赘述，示例代码如下：

class Solution {
public:int numSquares(int n) {vector<int> squares;for (int i = 1; i * i <= n; i++) {squares.push_back(i * i);}int m = squares.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX));for (int i = 0; i <= m; i++) {dp[i][0] = 0;}for (int i = 1; i <= m; i++) {int square = squares[i - 1];for (int j = 1; j <= n; j++) {dp[i][j] = dp[i - 1][j];if (j >= square && dp[i][j - square] != INT_MAX) {dp[i][j] = min(dp[i][j], dp[i][j - square] + 1);}}}return dp[m][n];}
};

leetcode 1449 数位成本和为目标值的最大数字

        这是一道非常经典的完全背包问题，也曾出现在一线互联网大厂的面试手撕中。对于这道题目来说，当我看到总成本正好等于target这个点，我就会往背包问题的方向考虑了。实际上我们发现题干中并没有对数字出现的次数作出限制，悄咪咪的看一眼测试用例发现也存在数字重复的情况，说明数字是可以无限次选的，也就是说这是一道完全背包，定下解题的大思路后我们来仔细分析一下。定义dp[i][j]的含义是选择前i个元素，能够使得总成本正好为j时，所获得的最大数字。首先我们来建边，当i==0时，假如说j!=0，也就意味着前面没有元素，但是你让我凑出来j的成本，这肯定是天方夜谭啊！是一种非法状态，我们把所有非法状态都标为“!”，可以初始化整张dp表都是非法状态。状态转移方程很好理解，和之前完全背包的模板提完完全全一个套路，不过有一些在这道题中必须注意的边界条件我需要多说两句：首先数位i+1才对应成本cost[i]，这是因为cost[i]是从0开始数的，我们必须注意到这个数位的偏移转换，但是实际上写的时候，如果设定循环自i到n的话，就不能是i+1~cost[i]，而必须是i~cost[i-1]，因为访问cost[n]的行为是非法的！其次就是我们需要选出“数值最大”的这个字符串来，一种实现方式是实现个外置比较函数里面调用，当然我的做法是通过字典序来搞。示例代码如下：

class Solution {
public:string largestNumber(vector<int>& cost, int target) {int n=cost.size();vector<vector<string>> dp(n+1,vector<string>(target+1,"!"));for (int i=0; i<=n; i++){dp[i][0] = "";}for(int i=1;i<=n;i++){for(int j=0;j<=target;j++){dp[i][j]=dp[i-1][j];int c = cost[i-1]; if(j>=c && dp[i][j-c]!="!"){string candidate= char('0'+i) + dp[i][j-c]; if(dp[i][j]=="!"||candidate.size()>dp[i][j].size()||(candidate.size()==dp[i][j].size()&&candidate>dp[i][j])){dp[i][j]=candidate;}}}}return dp[n][target]=="!"?"0":dp[n][target];}
};

leetcode 3592 硬币面值还原

        这道题目是后面加上来的，实在是不想放过这么好的一道题，思考过程中我参考了灵神的题解，深感这个思路巧妙至极！这是完全背包模板题leetcode 322的反向构造，背包问题是根据硬币面值算方案数量，而这道题是根据方案数量还原硬币面值。建议大家读完题目先好好看看测试用例1，这样就能对题意建立充分的理解。题设给出来的numWays数组其实就是一个完全背包数组。方便起见，这里我直接截图leetcode的输入输出解释部分，我们对照着来看：

        通过上表我们可以很清晰的了解方案数是怎么凑出来的，我们假设最终要返回的硬币数组为coins，那么numWays的最直接含义就是用完整集合 coins 能凑出和为 i 的方案数。首先我们解题需要有个切入点，numWays[2]==1，而numWays[1]==0，这代表什么？这其实就代表着一定存在面值为2的硬币，且当前场景下硬币面值最小为2！既然如此，对于任何可以用我们现有面值能凑出来的金额，一定有能利用面值2的方案，这个结论通过观察上表也很容易得出。

        假如我们当前只有面值为2的硬币，我们可以得出如下的完全背包数组：dp=[1,0,1,0,1,0,1,0,1,0,1]，注意下标就代表着需要凑出的金额，比如说dp[10]==1就代表着只通过面值为2的硬币凑出10的金额只有一种方案，就是通过5枚面值为2的硬币。这里有一个非常容易令人迷惑的点我要介绍下，实际上在代码实现的时候，我们要把numWays[0]初始化为1！这样才能统一dp和numWays数组的下标，否则容易看乱。

        此时我们来进行讨论：如果numWays[i]==dp[i]，就说明“完整集合coins” 里能凑出和为 i 的方案，数量和我们现在用小的元素凑出来的数量完全一样。也就是说，coins里面没有一个值为i的新元素来“贡献”出一个新的方案。比如numWays[2]==dp[2]==1，这就说明coins数组中没有一个额外的面值来贡献新方案了！而如果numWays[i]==dp[i]+1,说明i可以自己作为一个单独的数，贡献一个新方案，此时我们可以断定coins中必有i！我们把i放入coins中之后用i继续更新dp。比如numWays[4]==dp[4]+1==2，那么我们可以断定4一定可以作为一个单独的数字来贡献一个新方案，即coins里一定有面值为4的硬币，此时coins数组为[2,4]。我们再用4来更新前面的dp数组如下：dp=[1,0,1,0,2,0,2,0,3,0,3]。如果前两种情况都没中，那说明numWays不可能来源于coins，返回空即可。后续同理，我们会发现numWays[6]==dp[6]+1==3，所以也一定存在面值为6的硬币，继续用6来更新dp，以此类推...直到更新到i=10时，返回此时的coins数组就是答案！示例代码如下：

class Solution {
public:vector<int> findCoins(vector<int>& numWays) {int n=numWays.size();vector<int> dp(n+1), coins;dp[0]=1;for(int i=1;i<=n;i++){int ways=numWays[i-1];if(ways==dp[i]){continue;}if(ways-1!=dp[i]){return {};}coins.push_back(i);for (int j=i;j<=n;j++){dp[j]+=dp[j-i];}}return coins;}
};

三.分组背包

        相信通过前面的介绍和例题的操演，朋友们已经熟悉了0/1背包和完全背包这两种背包DP的模型。分组背包将货物分成若干组，每组里面有若干个货物。和0/1背包一样，分组背包也是只能选一次，但是是在每组物品至多选一次。其余场景都和0/1背包问题的题设完全相同。在分组背包问题中，dp[i][j]的含义是只考虑前i组货物，并且容量不超过j的前提下，所获得的最大价值。理由和0/1背包，完全背包完全一致。原理和0/1背包一致，当我们面对第i组物品时，我们如果不选这一组的任何物品，价值就是dp[i-1][j]。选择这一组中的某一个物品k(体积cost[i][k]，价值value[i][k])，价值就是dp[i-1][j-cost[i][k]] + value[i][k]。我们只需在这些情况中选最大值即可，我们可以整理出如下的状态转移方程：

dp[i][j] = max(
    dp[i-1][j],                           // 不选第 i 组
    max_{k ∈ group i, cost[i][k] ≤ j} { dp[i-1][j-cost[i][k]] + value[i][k] }
)

根据状态转移方程可以总结出下面的模板代码：

class solution{
public:int grouped_backpack(vector<vector<int>>&cost,vector<vector<int>>&value,int m,int t){vector<vector<int>> dp(m+1,vector<int>(t+1,0));for(int i=1;i<=m;i++){for(int j=0;j<=t;j++){ // 先考虑不选这一组的情况dp[i][j]=dp[i-1][j];for(int k=0;k<cost[i-1].size();k++){if(j-cost[i-1][k]>=0){dp[i][j]=max(dp[i][j],dp[i-1][j-cost[i-1][k]]+value[i-1][k]);}}}}return dp[m][t];}
};

leetcode 1155 掷骰子等于目标和的方法数

        这道题我觉得几乎就是分组背包的模板题了，就代码实现难度来说没有什么特别值得我们来详细讲的点，重点在于我们如何从题目中提取有效信息，从而将这道题目与分组背包问题建立起联系。题设中有n个骰子，每个骰子k个面，凑出target的目标和，其实看字眼很容易想到背包模型。和前面0/1背包最大的区别就在于，实际上这里存在一个分组，每个骰子其实就是一个“组”，也就是说在这个场景中存在n组。每个骰子只能投一次，也就是说每组中只会产生一个数。那么这个问题的dp[i][j]就代表着只考虑前i个骰子，在目标和刚好等于j时的方法数。示例代码如下：

class Solution {
public:int numRollsToTarget(int n, int k, int target) {const int MOD=1e9+7;vector<vector<int>> dp(n+1,vector<int>(target+1,0));dp[0][0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=target;j++){for(int x=1;x<=k;x++){if(j-x>=0){dp[i][j]=(dp[i][j]+dp[i-1][j-x])%MOD;}}}}return dp[n][target];}
};

leetcode 2218 从栈中取出K个硬币的最大面值和

        这道题有一定难度，可谓是相当经典的一道hard水准的大厂手撕题了。实际上这道题还是比较容易联想到分组背包模型的，因为明摆着可以按照不同的栈进行分组，而栈结构正是我们这道题目的关键所在，我们只能从栈顶连续往下取！这里有个很严重的误区，有人会想：分组背包要求的是每个组里只能选一次，可是在这个问题中同一个栈里我可以取很多数，甚至可以在次数允许的情况下取光。但关键之处就在这里，由于栈结构的特性限制，虽然可以取多个，但取的方式是固定顺序的前缀！你决定的东西其实是“在这个栈中取几个数”！很显然，我们应该将前缀和作为一个关键的参考指标，所以我们需要对栈中的元素进行求前缀和的预处理。由此我们就可以定义dp[i][j]的含义为在前i组栈中，取j个硬币的最大面值和，此时就可以套用分组背包问题的模板了，后面的过程同理，此处不再赘述。示例代码如下：

class Solution {
public:int maxValueOfCoins(vector<vector<int>>& piles, int k) {int n = piles.size();vector<vector<int>> dp(n + 1, vector<int>(k + 1, 0));for (int i = 1; i <= n; i++) {// i从1组开始(自己的设定)，但题目中的piles是从下标0开始// 所以来到i的时候要注意偏移量vector<int> team = piles[i - 1];int t = min((int)team.size(), k); // 确保t是int类型// 预处理前缀和加速计算vector<int> preSum(t + 1, 0);for (int j = 0, sum = 0; j < t; j++) { sum += team[j];preSum[j + 1] = sum;}for (int j = 0; j <= k; j++) { dp[i][j] = dp[i - 1][j]; for (int l = 1; l <= min(t, j); l++) { dp[i][j] = max(dp[i][j], dp[i - 1][j - l] + preSum[l]);}}}return dp[n][k];}
};

        以上就是我学习背包DP相关问题的一些心得体会，算法类的文章会随时更新，随时添加进去一些我发现的真题好题给大家分享。最重要的还是记清楚各种背包问题的题设，场景，条件，刷题培养题感，其次就是多见一些转换的思路，能够用最快的速度来定位问题的解法。有不当之处欢迎大家批评指正，我们一起成长！