利用BFS解决拓扑排序问题

在引入拓扑排序之前，我们先介绍几个概念

有向无环图

其本质是一个图，但特别的是，图上的每一个点都对应着方向（指向下一个可以走向的点），同时还要保证：图上的点的指向不可以形成一个环。

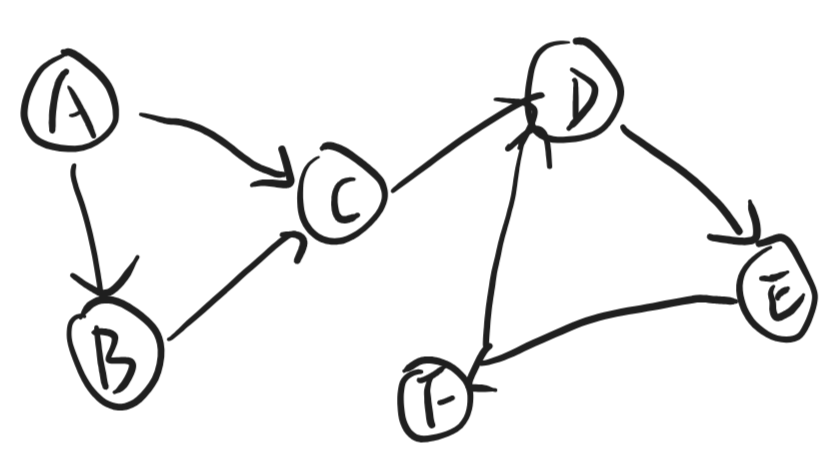
ABC就符合，因为BC无法回到A，然而DEF不符合，形成了环

入度，一个点被指向的个数

出度：一个点指向的个数

比如A的入度0出度2，C入度2出度1.

AOV网：顶点活动图

在有向无环图中，用顶点来表示一个活动，用边来表示活动的先后顺序的图结构。

拓扑排序：

在图中标识着做这件事的各个步骤，找到做这件事的顺序就是拓扑排序。我们需要知道的是，拓扑排序的结果可能不是唯一的（可能相同入度的优先级相同）

如何进行排序？

先找出图中入读为0的点，然后输出

删除与该点连接的边

重复上述操作，知道图中没有点或者没有入度为0的点（有可能有环）为止。

如何实现排序？

用队列进行BFS

先把入度为0的点都加入到队列中，当队列不为空时：
拿出队头元素放到最终结果中，删除与该元素相连的边

判断与删除边相连的点的入度，为0加入到队列中

实战——课程表

我们给几组数据模拟一下图

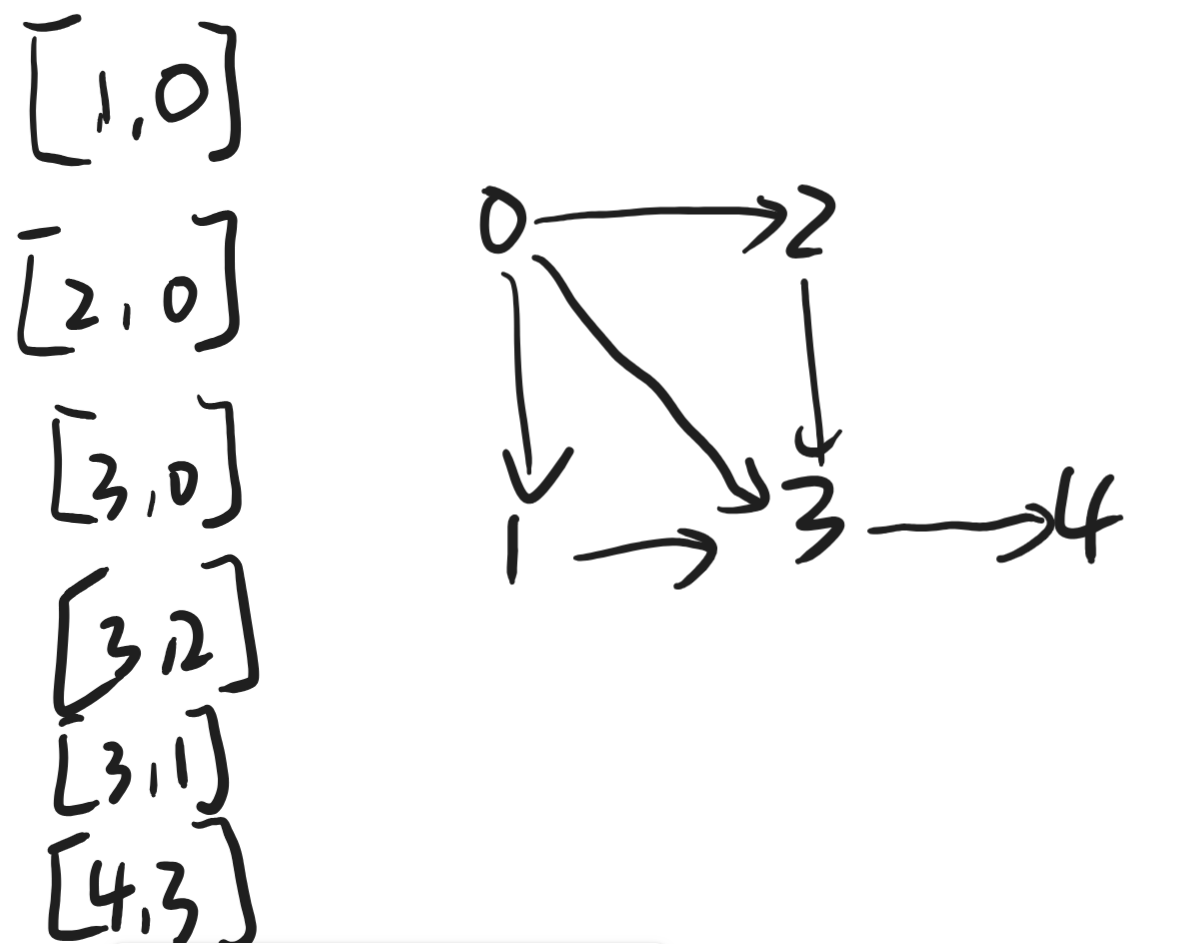
问题在于：我们如何去创建这个图？？？

这里我们给出两种方案：

vector<vector<int>> :n行，用[n][m]来记录第n个点有m的入度（只需要在n行插入m个数据即可）

unordered_map<int ,vector<int>>:first用于记录节点，second中插入该点的所有入度点。

这里我们采用第二种方案，具体细节在代码中注释。

bool canfinish(int n,vector<vector<int>>& pre)
{//创建图unordered_map<int,vector<int>> edges;//first存点，second存该点的出度都指向哪点//例：1->2,1-3,1-4//就是1的hash存放vector(2,3,4)。vector<int> in(n);//存放每一个点的入度//放入入度for(auto & e:pre){int a=e[0],b=e[1];//b->aedges[b].push_back(a);//存出度in[a]++;//a有了入度}queue<int>q;for(int i=0;i<n;i++){//把入度为0的点放入队列if(in[i]==0) q.push(i);}//拓扑排序while(q.size()){int t=q.front();q.pop();//把该点的所有出度拿出来遍历for(int a:edges[t]){in[a]--;//入度减一，删除连接线if(in[a]==0) q.push(a);}}//出循环，如果in中还有值证明图中有环for(int i=0;i<n;i++){if(in[i]) return false;}return true;}