博弈论 之 巴什博奕,尼姆博弈,威佐夫博弈,斐波那契博弈
最近开始补题学习,第一个要学的是博弈论
序章
先说一下巴什博奕
两个玩家轮流行动且游戏方式一致
两个玩家对状况完全了解
游戏一定会在有限步数内分出胜负
游戏以玩家无法行动结束4.
博弈的双方都被认为是神之个体,因为所有玩家对状况完全了解,且充分为自己打算,绝对理性当局面确定,结果必然注定,并且没有任何随机的成分游戏中的每一个状态,最终导致的结果也必然注定,只有必胜态、必败态,两种状态这一类博弈问题的结果没有任何意外,一方可以通过努力去改变结果是不可能的,这一点是反直觉的
一个最基础的巴什博奕
巴什博弈(Bash Game)一共有n颗石子,两个人轮流拿,每次可以拿1~m颗石子拿到最后一颗石子的人获胜,根据n、m返回谁赢
先直接说结论 如果n能整除m+1那么后手的人赢 , 如果不能整除则先手赢
因为如果一个人每次遇到的要拿的情况都是剩下m+1的倍数个物品,当最后一次遇到m+1那他也最多只能拿m个,最少拿1个,而下一个人就必定能一次性拿完,而且我们可以保证每个人是绝对聪明的,如果一个人有这个机会,他是可以使另一个永远面对拿m+1倍数个物品,所以我们就可以得到这个结论如果n能整除m+1那么后手的人赢 , 如果不能整除则先手赢
其实总结一下,也就是我们要让对方先面临不能触碰到的次数的倍数个物品,他就输了,因为我们是绝对聪明的
P4018 Roy&October之取石子
P4018 Roy&October之取石子 - 洛谷
题目背景
Roy 和 October 两人在玩一个取石子的游戏。
题目描述
游戏规则是这样的:共有 n 个石子,两人每次都只能取 p^k 个( p 为质数,k 为自然数,且 pk 小于等于当前剩余石子数),谁取走最后一个石子,谁就赢了。
现在 October 先取,问她有没有必胜策略。
若她有必胜策略,输出一行
October wins!;否则输出一行Roy wins!。输入格式
第一行一个正整数 T,表示测试点组数。
第 2 行∼ 第 T+1 行,一行一个正整数 n,表示石子个数。
输出格式
T 行,每行分别为
October wins!或Roy wins!。输入输出样例
输入 #1复制
3 4 9 14输出 #1复制
October wins! October wins! October wins!说明/提示
对于 30% 的数据,1≤n≤30;
对于 60% 的数据,1≤n≤106;
对于 100% 的数据,1≤n≤5×107, 1≤T≤105。
(改编题)
思路
我们可以看题就是p的k次方使我们可以轮流拿的物品个数,p是质数,k是自然数,0,1,2,3.....
2^0是1,2^1,3^1,2^2,5^1,到6发现无法得到6然后7^1,2^3......,我们可以发现除了6的倍数我们都可以得到,把这个情况带入进上面讲的内容,是不是这个6就相当于m+1然后只要让对方永远处于6的倍数个物品对方就一定输,所以也就是看n是否能被6整除就好,接下来看代码
#include<bits/stdc++.h>
using namespace std;
int main(){int t;cin>>t;while(t--){int n;cin>>n;if(n%6){cout<<"October wins!"<<endl;}else{cout<<"Roy wins!"<<endl;}}
}P1288 取数游戏 II
P1288 取数游戏 II - 洛谷
题目描述
有一个取数的游戏。初始时,给出一个环,环上的每条边上都有一个非负整数。这些整数中至少有一个 0。然后,将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏,两人轮流取数,取数的规则如下:
- 选择硬币左边或者右边的一条边,并且边上的数非 0;
- 将这条边上的数减至任意一个非负整数(至少要有所减小);
- 将硬币移至边的另一端。
如果轮到一个玩家走,这时硬币左右两边的边上的数值都是 0,那么这个玩家就输了。
如下图,描述的是 Alice 和 Bob 两人的对弈过程(其中黑色节点表示硬币所在节点)。
各图的结果为:
- A:轮到 Alice 操作;
- B:轮到 Bob 操作;
- C:轮到 Alice 操作;
- D:轮到 Bob 操作。
D 中,轮到 Bob 走时,硬币两边的边上都是 0,所以 Alice 获胜。
现在,你的任务就是根据给出的环、边上的数值以及起点(硬币所在位置),判断先走方是否有必胜的策略。
输入格式
第一行一个整数 N (N≤20),表示环上的节点数。
第二行 N 个数,数值不超过 30,依次表示 N 条边上的数值。硬币的起始位置在第一条边与最后一条边之间的节点上。
输出格式
仅一行。若存在必胜策略,则输出
YES,否则输出NO。输入输出样例
输入 #1复制
4 2 5 3 0输出 #1复制
YES输入 #2复制
3 0 0 0输出 #2复制
NO
思路:
就是说有个环,里面有n个边,然后里面至少有1个边的边权为0,然后我们从第一个节点走,就像下面这个一样,从第一个开始走,每选择走一个边,这个边就必须至少对这个边的边权减1,然后我们不能走边权位为0的边,当最后一个人要走时发现两边都是0,那他就输了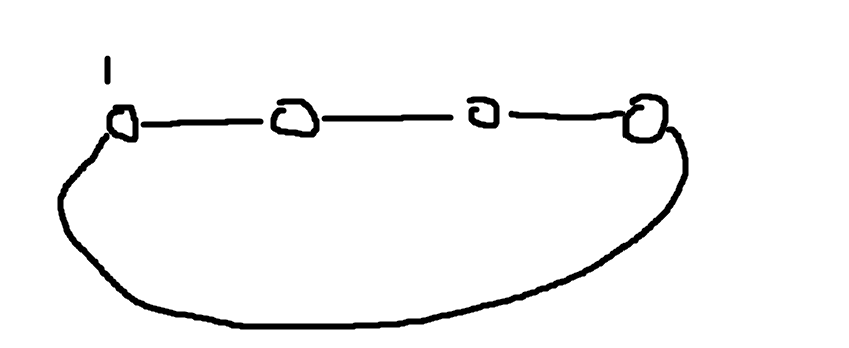
我们可以发现当你直接把一个边走了,之后这个边全减完,那我们就发现不能往回走了,只能往前,,,现在有一个情况就是前面的边如果是0,那如果对方不直接走完,我们再往回走,直接减完边权,那他这时候就无法再走了,就输了所以 我们先手一定要每次都减完路,这样就是保证了每个人绝对聪明 那我们就容易得到从右或走开始走只要这两条路有一个到达第一个边权为0的路是偶数编号,先手就一定赢,我们看代码
#include<bits/stdc++.h>
using namespace std;
int main(){int n;cin>>n;int arr[n+100];for(int i=1;i<=n;i++){cin>>arr[i];}int f=0;for(int i=1;i<=n;i++){if(arr[i]==0&&i%2==0){cout<<"YES";return 0;}else if(arr[i]==0&&i%2!=0){f++;break;}} for(int i=n;i>=0;i--){if(arr[i]==0&&(n-i+1)%2==0){cout<<"YES";return 0;}else if(arr[i]==0&&(n-i+1)%2!=0){f++;break;}}if(f==2) cout<<"NO";return 0;}P1290 欧几里德的游戏
P1290 欧几里德的游戏 - 洛谷
题目描述
欧几里德的两个后代 Stan 和 Ollie 正在玩一种数字游戏,这个游戏是他们的祖先欧几里德发明的。给定两个正整数 M 和 N,从 Stan 开始,从其中较大的一个数,减去较小的数的正整数倍,当然,得到的数不能小于 0。然后是 Ollie,对刚才得到的数,和 M,N 中较小的那个数,再进行同样的操作……直到一个人得到了 0,他就取得了胜利。下面是他们用 (25,7) 两个数游戏的过程:
- 初始:(25,7);
- Stan:(11,7);
- Ollie:(4,7);
- Stan:(4,3);
- Ollie:(1,3);
- Stan:(1,0)。
Stan 赢得了游戏的胜利。
现在,假设他们完美地操作,谁会取得胜利呢?
输入格式
本题有多组测试数据。
第一行为测试数据的组数 C。 下面 C 行,每行为一组数据,包含两个正整数 M,N(M,N<231)。
输出格式
对每组输入数据输出一行,如果 Stan 胜利,则输出
Stan wins;否则输出Ollie wins。输入输出样例
输入 #1复制
2 25 7 24 15输出 #1复制
Stan wins Ollie wins说明/提示
1≤C≤6。
思路:
我先说一下先手必胜情况,就是在a=kb情况,先手可以直接减去k倍的b然后就赢了
然后还有就是a/b>=2,这样就能保证先手有多个选择,先手可以把给后手留下a变成比b小的值,也可以留下比b大但不超过2b的情况,这样留下两种情况,第一种情况和第二种情况之间只是第一种情况多减去一个b,如果第一种情况能让后手赢,那我们就留下第二种情况给后手,然后后手必续减一个b,我们的先手就能得到第一种情况的状态了,那先手就赢了,反之第二种情况能让后手赢,那我们就直接给就给他留第一种情况,先手必赢,我们先手永远掌控着控制权
之后就是死磕情况 a/b<=1,我们没法去控制,我们只能一次一次减一个最小值,然后看谁最后赢,这个情况我们直接用递归来计算谁赢
#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
// 参数 a 和 b 满足 a >= b
bool solve(int a,int b){// 如果 a 是 b 的倍数,当前玩家可以直接减去多个 b 得到 0,获胜if(a%b==0){return true;}// 如果 a >= 2b,当前玩家可以强制获胜if(a>=2*b){return true;}// 否则,当前玩家只能减去 b 一次,得到状态 (b, a - b)// 胜负取决于对手在状态 (b, a - b) 下的表现// 如果对手在 (b, a - b) 下必败,则当前玩家获胜,否则失败return !solve(b,a-b);
}
signed main(){int C;cin>>C;while(C--){int M,N;cin>>M>>N;// 确保 M 是较大的数if(M<N){swap(M,N);}if(solve(M,N)) {cout<<"Stan wins"<<endl;}else{cout<<"Ollie wins"<<endl;}}return 0;
}P4702 取石子
P4702 取石子 - 洛谷
题目描述
Alice 和 Bob 在玩游戏。
他们有 n 堆石子,第 i 堆石子有 ai 个,保证初始时 ai≤ai+1(1≤i<n)。现在他们轮流对这些石子进行操作,每次操作人可以选择满足 ai>ai−1(a0 视为 0)的一堆石子,并从中取走一个。谁最后不能取了谁输。Alice 先手,他们都使用最优策略,请判断最后谁会取得胜利。
输入格式
第一行一个整数 n(1≤n≤100),表示石子堆数。
接下来一行 n 个数,第 i 个数为 ai(1≤ai≤109),意义如上所述。
输出格式
"Alice" 或 "Bob",表示谁会赢。
输入输出样例
输入 #1复制
1 1输出 #1复制
Alice输入 #2复制
1 2输出 #2复制
Bob
思路
题说的可麻烦,说啥选只能选ai>ai-1的石头堆,其实这就意思是所有石头堆咱都能拿,那也就是我们直接把所有石头堆都加起来,看是偶数奇数就行了
#include<bits/stdc++.h>
using namespace std;
#define int long long
signed main(){int n;cin>>n;int a[n+10];int ans=0;for(int i=1;i<=n;i++){cin>>a[i];ans+=a[i];}if(ans%2==0){cout<<"Bob";}else{cout<<"Alice";}
}接下来讲一下
尼姆博弈
先看一下模版题
P2197 【模板】Nim 游戏
P2197 【模板】Nim 游戏 - 洛谷
题目描述
甲,乙两个人玩 nim 取石子游戏。
nim 游戏的规则是这样的:地上有 n 堆石子(每堆石子数量小于 104),每人每次可从任意一堆石子里取出任意多枚石子扔掉,可以取完,不能不取。每次只能从一堆里取。最后没石子可取的人就输了。假如甲是先手,且告诉你这 n 堆石子的数量,他想知道是否存在先手必胜的策略。
输入格式
本题有多组测试数据。
第一行一个整数 T (T≤10),表示有 T 组数据
接下来每两行是一组数据,第一行一个整数 n,表示有 n 堆石子,n≤10e4。
第二行有 n 个数,表示每一堆石子的数量.
输出格式
共 T 行,每行表示如果对于这组数据存在先手必胜策略则输出
Yes,否则输出No。输入输出样例
输入 #1复制
2 2 1 1 2 1 0输出 #1复制
No Yes
思路
给了n堆石子,每一堆都有数量,然后两个人轮流可以一次拿无数个石子(对于一堆石子来说),然后谁最后拿完所有石子谁赢
先说结论,对所有石子堆异或,求出来的和如果不等于0则先手赢,反之后手赢
看每个石子堆的石子数量的二进制
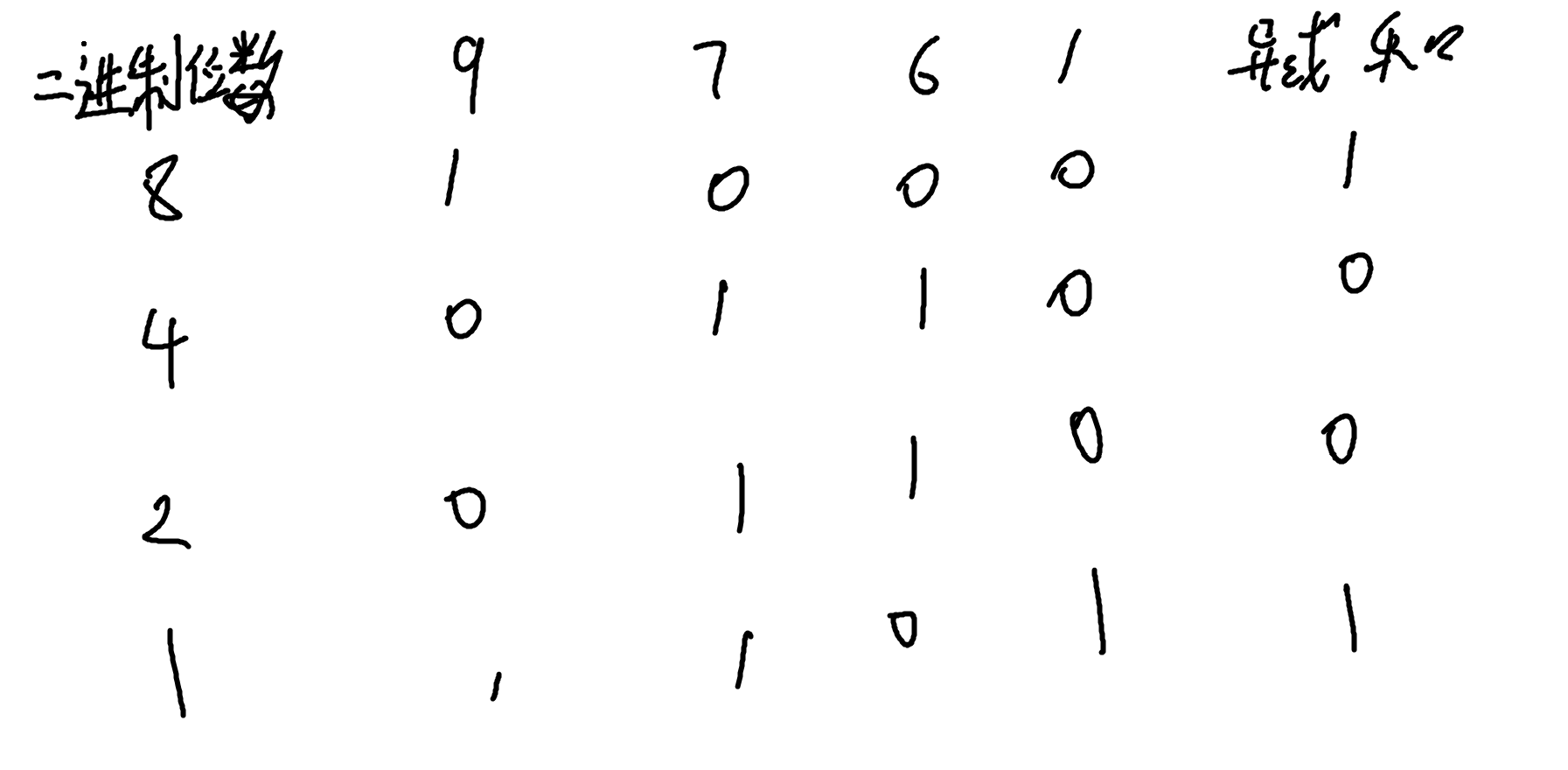

看着两个例子,我们只需看每一位二进制的异或和,然后我们再看最高位的异或和1,找到对应的数,看第1个图,最高位对应的数在9里面,我们就可以对9操作然后使得整个异或和为0,我们对这个石子堆拿走9个石子堆这样整个异或和就为0了
再看第二个图,异或和1最高位对应的在7里面,我们就只需要在这个石子堆里面拿走6,这样整个异或和就为0了,
所以我想说的是当所有石子堆异或和不为0时候我们可以对其进行任意操作可以将其变为0,然后还有一个重点就是当石子全部被拿走我们的石子堆的异或和也是0,所以我们在进行数次操作后,一定会转移到全部石子堆数量为0的情况,然后当一个人拿到的状态是所有石子堆异或和为0时候,对其进行拿走任意石子,一定会变成石子堆异或和不为0的情况,
所以当先手接到初始时候石子堆异或和不为0的情况,先手就可以对其操作让其变为0,然后给后手,这样进行数次操作,后手永远接收到的情况是异或和为0,那么总会到达所有石子堆都为0的情况
综上所述,当石子堆的初始异或和不为0,先手必胜,反之后后手必胜
看代码
#include<bits/stdc++.h>
using namespace std;
int t,n,s;
int main(){cin>>t;while(t--){s=0;cin>>n;for(int i=0;i<n;i++){int k;cin>>k;s^=k;} if(s==0){cout<<"No"<<endl;}else{cout<<"Yes"<<endl;}}}P4279 [SHOI2008] 小约翰的游戏
P4279 [SHOI2008] 小约翰的游戏 - 洛谷
题目描述
小约翰经常和他的哥哥玩一个非常有趣的游戏:桌子上有 n 堆石子,小约翰和他的哥哥轮流取石子,每个人取的时候,可以随意选择一堆石子,在这堆石子中取走任意多的石子,但不能一粒石子也不取,我们规定取到最后一粒石子的人算输。
小约翰相当固执,他坚持认为先取的人有很大的优势,所以他总是先取石子,而他的哥哥就聪明多了,他从来没有在游戏中犯过错误。小约翰一怒之前请你来做他的参谋。自然,你应该先写一个程序,预测一下谁将获得游戏的胜利。
输入格式
本题的输入由多组数据组成,第一行包括一个整数 T(1≤T≤500),表示输入总共有 T 组数据。
每组数据的第一行包括一个整数 N(1≤N≤50),表示共有 N 堆石子,接下来有 N 个不超过 5000 的整数,分别表示每堆石子的数目。
输出格式
对于每组数据,如果约翰能赢得比赛,则输出
John,否则输出Brother,请注意单词的大小写。输入输出样例
输入 #1复制
2 3 3 5 1 1 1输出 #1复制
John Brother说明/提示
- 对于 40% 的数据,T≤250;
- 对于 100% 的数据,T≤500。
思路
跟上题不一样的是,这次是当最后拿完石子的人算输了
这题我想先说一下,就是他肯定不是跟上题反着就对了,因为上题说的是,先手拿到异或不为0情况然后一直给后手的情况是异或为0,然后后手也没办法,无论怎么操作后手拿走石子后,结果一定是异或不为0,所以这样弄,最后一定是后手输,
而这题,如果是想让先手拿到异或为0的情况,那先手操作后给后手的是异或不为0的情况,后手既可以把情况变成异或都为0,也可以不这样操作,所以这样思考问题是错误的,主动权就变成后手了,所以接下来我讲正确做法
情况1 每堆石子的数量都为1

我们可以发现这种情况只要看石子堆数是奇数还是偶数,当奇数时先手必输,当偶数时先手必赢
情况2 只有一堆是数量大于1其他都是1,这时候先手必胜

因为我们先手可以选择拿这个5,拿4个这样后手的状态就是剩下3个,这样轮过去后先手赢,我们也可以直接拿5(当总共有偶数堆时候),然后这样再给后手剩下奇数堆,后手就输了
情况3 就是不只有一个大于1的石子堆,就是普通情况,我们已知情况2的异或一定不为0,所以我们只要保证先手永远拿到异或不为0,然后给后手的情况变成异或和为0,这样依次轮流进行,最终先手一定会遇到情况2,然后这时候遇到情况2,那先手就必胜了,
剩下看代码就行了
#include<bits/stdc++.h>
using namespace std;
int t,n,s;
int main(){cin>>t;while(t--){s=0;int sum=0;cin>>n;for(int i=0;i<n;i++){int x;cin>>x;sum+=x;s^=x;}if(sum==n){if(n%2==0){cout<<"John"<<endl;}else{cout<<"Brother"<<endl;}}else{if(s!=0){cout<<"John"<<endl;}else{cout<<"Brother"<<endl;}}}}P6487 [COCI 2010/2011 #4] HRPA
P6487 [COCI 2010/2011 #4] HRPA - 洛谷
题目描述
有 n 枚石子。两位玩家定了如下规则进行游戏:
- Mirko 先取一次,Slavko 再取一次,然后 Mirko 再取一次,两人轮流取石子,以此类推;
- Mirko 在第一次取石子时可以取走任意多个;
- 接下来,每次至少要取走一个石子,最多取走上一次取的数量的 2 倍。当然,玩家取走的数量必须不大于目前场上剩余的石子数量。
- 取走最后一块石子的玩家获胜。
双方都以最优策略取石子。Mirko 想知道,自己第一次至少要取走几颗石子最终才能够获胜。
输入格式
输入一行一个整数 n,表示石子的数量。
输出格式
输出一行一个整数,表示 Mirko 最少取多少石子可以保证获胜。
输入输出样例
输入 #1复制
4输出 #1复制
1输入 #2复制
7输出 #2复制
2输入 #3复制
8输出 #3复制
8说明/提示
样例 1 解释
对于这个样例,Mirko 第一次可以取 1/2/3/4 个。虽然他取 4 个会直接赢得比赛,但这并不是最少的。最少的方案是取走 1 个。这样 Slavko 只能取走 1 个或者 2 个。无论选择哪种,Mirko 下一步都能取走所有的石子并获胜。
数据规模与约定
对于 100% 的数据,保证 2≤n≤1015。
说明
题目译自 COCI2010-2011 CONTEST #4 T6 HRPA。
思路
这是个斐波那契博弈
我们先定下,先手一次性不拿完,然后发现n=1,必输,n=2必输,n=3必输,n=5,拆分成2和3,发现依旧必输,然后我们看13举例子
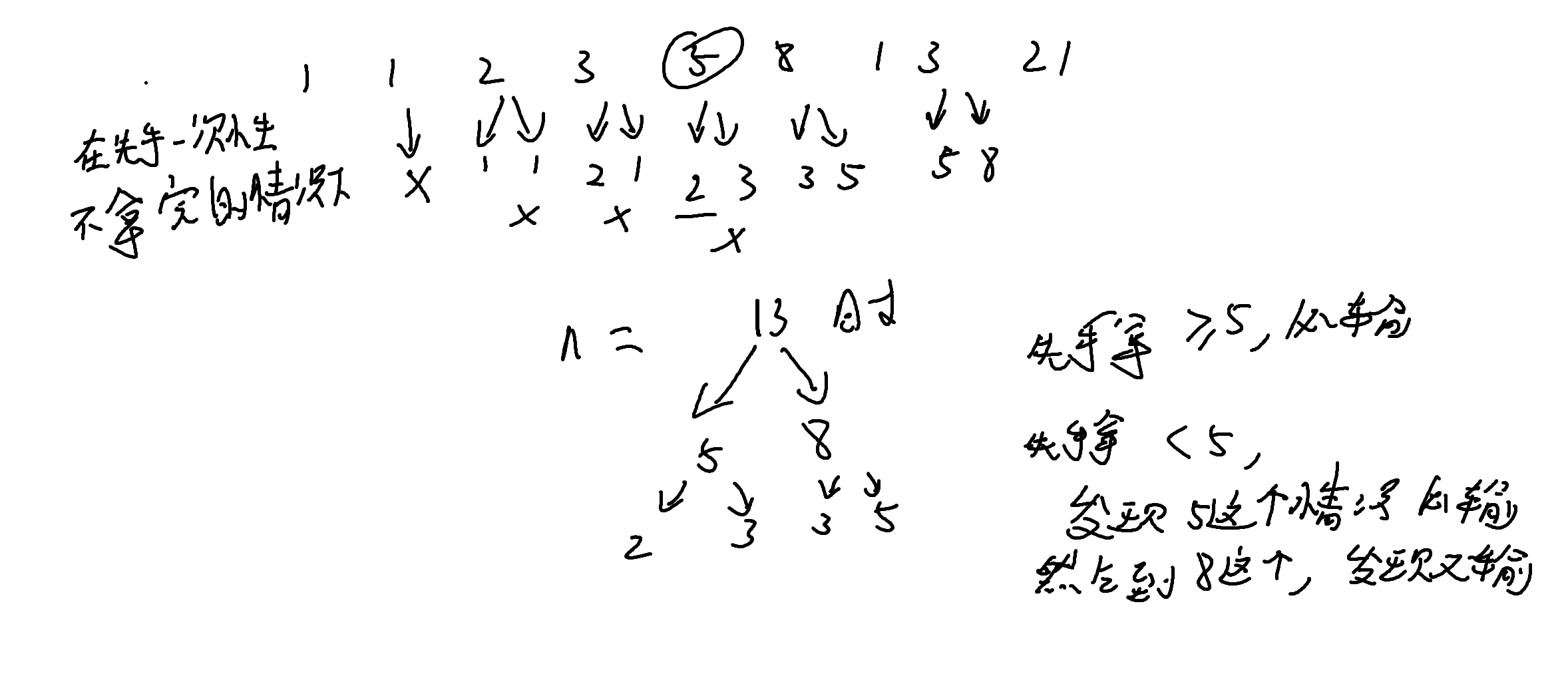
这上面情况是当n是斐波那契数
下面讲不是斐波那契数
我们可以知道不是斐波那契数他可以别拆成若干不相邻的斐波那契数之和,比如4=3+1,6=5+1,7=5+2等等,然后我们可以发现两个不相邻的斐波那契数大的那个一定比离他最近且不大于他的那个数小两倍以上,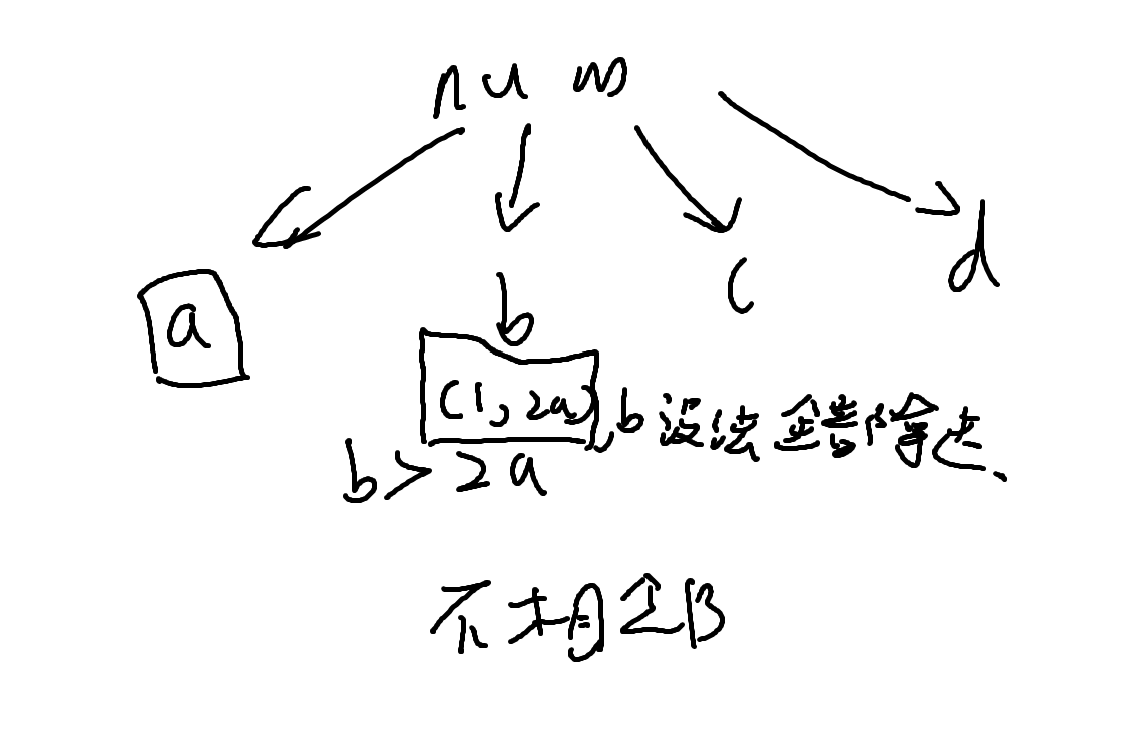
就是a先手拿走完,b这堆就后手无法全部被拿走完,然后这不就是刚刚讲的n是斐波那契数的情况吗,这时的后手就变成了刚刚讲过的斐波那契数里的先手(而先手必输),所以最后就可以得到先手必赢了,然后这个a就是我们最少要拿走的数量对吧,还有就是这个题的数据开大点
看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int maxn=1e16;
int fib[110];
int maxfib(int n){int a=0,b=1,c=1;while(c<=n){a=b;b=c;c=a+b;}return b;//b是小于n的最大fib数
}
signed main(){int n;cin>>n;int ans=-1,find;while(n!=1&&n!=2){find=maxfib(n);if(n==find){ans=find;break;} else{n-=find;}}if(ans!=-1){cout<<ans;} else{cout<<n;}
}威佐夫博弈
威佐夫博弈(Wythoff Game)
有两堆石子,数量任意,可以不同,游戏开始由两个人轮流取石子游戏规定,每次有两种不同的取法1)在任意的一堆中取走任意多的石子2)可以在两堆中同时取走相同数量的石子最后把石子全部取完者为胜者现在给出初始的两堆石子的数目,返回先手能不能获胜
直接说结论
较小的一堆!=(大-小)*黄金分割比例,先手赢
较小的一堆==(大-小)*黄金分割比例,后手赢
都已经出现了黄金分割比例了,想都不用想这很难证明,直接记结论 博闻强识
P2252 [SHOI2002] 取石子游戏 |【模板】威佐夫博弈
P2252 [SHOI2002] 取石子游戏 |【模板】威佐夫博弈 - 洛谷
题目描述
有两堆石子,数量任意,可以不同。游戏开始由两个人轮流取石子。游戏规定,每次有两种不同的取法:一是可以在任意的一堆中取走任意多的石子;二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。现在给出初始的两堆石子的数目,你先取,假设双方都采取最好的策略,问最后你是胜者还是败者。
输入格式
输入共一行。
第一行共两个数 a,b,表示石子的初始情况。
输出格式
输出共一行。
第一行为一个数字 1,0 或 −1,如果最后你是胜利者则为 1;若失败则为 0;若结果无法确定则为 −1。
输入输出样例
输入 #1复制
8 4输出 #1复制
1说明/提示
数据范围
50% 的数据满足 a,b≤1000;
100% 的数据满足 a,b≤109。
思路
就按照上面写就行了
怎么说呢,那个黄金比例必须·用long double ,开根也必须是sqrtl要不然精度不够,服了我改半天
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a,b;
signed main(){long double split=(sqrtl(5.0)+1.0)/2.0;cin>>a>>b;int minx=min(a,b);int maxx=max(a,b);if(minx!=(int)((maxx-minx)*split)) cout<<1;else{cout<<0;}}