K-means 聚类算法:基于鸢尾花数据集的无监督学习全流程解析
K-means 聚类是无监督学习(Unsupervised Learning)领域最经典、最常用的算法之一,核心逻辑是通过 “距离度量” 将相似数据自动归为一类(簇),无需预先标注样本标签。本文以鸢尾花数据集为案例,从算法原理、代码实现、结果可视化到 K 值选择优化,完整拆解 K-means 聚类的应用流程。
一、项目背景与核心目标
1. 数据集介绍
本次使用的鸢尾花(Iris)数据集包含 150 条样本,每条样本含 4 个形态特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度)及 1 个类别标签(3 种鸢尾花品种:Iris-setosa、Iris-versicolor、Iris-virginica)。
注意:K-means 是无监督算法,建模时会忽略类别标签,仅通过特征相似度聚类,最终可对比聚类结果与真实标签验证效果。
2. 核心目标
- 掌握 K-means 聚类的核心原理(质心迭代、距离计算);
- 基于鸢尾花的 4 个特征,用 K-means 将样本聚为 3 个簇(对应真实 3 个品种);
- 学习高维数据可视化方法(PCA 降维),直观展示聚类结果;
- 理解 K 值选择的关键方法(肘部法、轮廓系数),解决 “如何确定最优簇数” 问题。
二、技术工具与环境准备
- 编程语言:Python 3.9
- 核心库说明:
库名 核心用途 pandas/numpy数据加载、结构化处理与数值计算 matplotlib/seaborn聚类结果可视化(散点图) sklearn.clusterK-means 聚类模型实现( KMeans)sklearn.decompositionPCA 降维(将 4 维特征降为 2 维,便于可视化) sklearn.metrics聚类性能评估(轮廓系数)
三、K-means 聚类核心原理铺垫
在实战前,先明确 K-means 的核心逻辑,帮助理解代码设计思路:
1. 算法核心思想
K-means 通过 “迭代更新簇中心(质心)” 实现聚类,目标是让簇内样本相似度最高,簇间样本相似度最低(用 “误差平方和 SSE” 量化)。
2. 完整迭代流程
K-means 算法的执行步骤可概括为 5 步,循环直至收敛:
- 确定 K 值:指定需要聚类的簇数(如本次案例 K=3,对应鸢尾花 3 个品种);
- 初始化质心:从数据集中随机选择 K 个样本作为初始簇中心(质心);
- 分配样本:计算每个样本到 K 个质心的距离(默认欧式距离),将样本分配到距离最近的簇;
- 更新质心:对每个簇,计算簇内所有样本在各特征维度的均值,作为新的质心;
- 判断收敛:对比新质心与旧质心,若质心位置无变化(或变化小于阈值),则聚类结束;否则返回步骤 3 继续迭代。
3. 关键概念解释
- 欧式距离:衡量高维空间中两点的直线距离,公式为 \(d(x,y)=\sqrt{\sum_{i=1}^{n}(x_i-y_i)^2}\)(n 为特征数)
- 误差平方和(SSE):簇内所有样本到其质心的距离平方和,SSE 越小说明簇内样本越集中,聚类效果越好;
- 收敛:质心位置不再变化,意味着样本分配结果稳定,算法停止迭代。
四、实战:K-means 鸢尾花聚类模型
1. 导入依赖库与环境配置
首先导入所需库,并配置中文显示(避免可视化乱码):
# 数据处理库
import pandas as pd
import numpy as np
# 可视化库
import matplotlib.pyplot as plt
# K-means与降维工具
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
# 其他工具
from numpy import nonzero, array
import warnings
warnings.filterwarnings('ignore') # 忽略警告信息# 环境配置:正常显示中文和负号
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False2. 加载并预处理数据集
K-means 是无监督算法,需提取特征矩阵并剔除类别标签,同时检查数据完整性:
# 加载本地鸢尾花数据集(需替换为你的文件路径)
iris = pd.read_csv(r"D:\Desktop\CC是小陈\Machine Learning\Iris.csv")# 1. 查看数据前5行,了解结构
print("=== 数据集前5行预览 ===")
print(iris.head())# 2. 提取特征矩阵(剔除最后一列类别标签)
columns = iris.columns # 获取所有列名
features = columns[:-1] # 前4列为特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度)
dataset = iris[features] # 特征矩阵(150行×4列)# 3. 数据基本信息(确认无缺失值)
print("\n=== 数据基本信息 ===")
print(f"特征矩阵维度:{dataset.shape}") # 输出:(150, 4)
print(f"缺失值统计:\n{dataset.isnull().sum()}") # 所有特征缺失值均为0,数据完整# 4. 保存原始标签(用于后续对比聚类结果,非建模使用)
original_labels = iris[columns[-1]].values # 真实品种标签
print(f"\n原始品种标签示例:{original_labels[:5]}") # 输出前5个标签数据预处理结论
- 数据集无缺失值,无需填充;
- 特征均为数值型(cm),但 K-means 对量纲敏感(如花瓣宽度 0.2-2.5cm,花萼长度 4.3-7.9cm),后续需标准化(原文未提及,补充此步骤可提升聚类效果);
- 原始标签仅用于验证聚类合理性,建模时不参与计算。
3. 特征标准化
K-means 基于距离计算样本相似度,若特征量纲差异大,会导致 “数值大的特征”(如花萼长度)主导距离计算。需通过标准化将所有特征转换为 “均值 = 0,标准差 = 1”:
# 导入标准化工具
from sklearn.preprocessing import StandardScaler# 初始化标准化器
scaler = StandardScaler()
# 对特征矩阵标准化
dataset_scaled = scaler.fit_transform(dataset)# 查看标准化后的数据(前5行)
print("\n=== 标准化后特征矩阵(前5行) ===")
print(pd.DataFrame(dataset_scaled, columns=features).head())4. 实现聚类结果可视化函数
鸢尾花特征为 4 维,无法直接可视化,需通过PCA 降维将 4 维特征压缩为 2 维,再绘制散点图展示聚类结果:
def draw_cluster(dataset, centers, labels, k, title="K-means聚类结果"):"""绘制K-means聚类结果散点图参数:dataset: 特征矩阵(可高维)centers: 簇中心(K×特征数)labels: 聚类标签(150个样本的簇归属)k: 簇数title: 图表标题"""# 将特征矩阵和簇中心降为2维(PCA)pca = PCA(n_components=2) # 降为2维dataset_2d = pca.fit_transform(dataset) # 特征矩阵降维centers_2d = pca.transform(centers) # 簇中心同步降维(使用相同的PCA参数)# 定义颜色列表(支持最多15个簇,满足大多数场景)colors = np.array(["#FF0000", "#0000FF", "#00FF00", "#FFFF00", "#00FFFF", "#FF00FF", "#800000", "#008000", "#000080", "#808000","#800080", "#008080", "#444444", "#FFD700", "#008080"])# 绘制聚类结果散点图plt.figure(figsize=(10, 8))# 绘制每个簇的样本for i in range(k):# 筛选出第i个簇的样本cluster_samples = dataset_2d[nonzero(labels == i)]# 绘制样本点(不同簇用不同颜色)plt.scatter(cluster_samples[:, 0], cluster_samples[:, 1],c=colors[i], marker='o', s=50, alpha=0.7, label=f'簇{i+1}')# 绘制簇中心(黑色×标记,突出显示)plt.scatter(centers_2d[:, 0], centers_2d[:, 1],c='black', marker='x', s=200, linewidth=3, label='簇中心')# 添加图表标签与图例plt.title(title, fontsize=14, pad=15)plt.xlabel('PCA维度1', fontsize=12)plt.ylabel('PCA维度2', fontsize=12)plt.legend(fontsize=10)plt.grid(linestyle='--', alpha=0.3)plt.show()函数逻辑解读
- PCA 降维:通过
PCA(n_components=2)将 4 维特征映射到 2 维空间,保留数据的主要信息(方差最大的方向); - 簇区分:不同簇用不同颜色标记,簇中心用黑色 “×” 突出,便于直观观察聚类效果;
- 通用性:支持任意高维数据,只需传入特征矩阵、簇中心和标签即可生成可视化图。
5. 执行 K-means 聚类
指定 K=3(对应鸢尾花 3 个品种),初始化模型并训练,最后调用可视化函数展示结果:
# 1. 指定簇数K(根据业务知识或先验信息设定,此处K=3)
k = 3# 2. 初始化K-means模型
# n_init=10:多次随机初始化质心(默认10次),选择SSE最小的结果,避免初始质心敏感问题
kmeans = KMeans(n_clusters=k, n_init=10, # 关键参数:增加初始化次数,提升结果稳定性random_state=42 # 固定随机种子,确保结果可复现
)# 3. 用标准化后的特征矩阵训练模型
kmeans.fit(dataset_scaled)# 4. 获取聚类结果
cluster_labels = kmeans.labels_ # 每个样本的簇归属(0、1、2)
cluster_centers = kmeans.cluster_centers_ # 簇中心(3×4维,对应4个特征)
sse = kmeans.inertia_ # 误差平方和(SSE),衡量聚类效果# 5. 打印聚类结果关键信息
print("\n=== K-means聚类结果 ===")
print(f"簇数K:{k}")
print(f"各簇样本数量:{np.bincount(cluster_labels)}") # 统计每个簇的样本数
print(f"误差平方和(SSE):{sse:.4f}") # 输出SSE,值越小聚类效果越好# 6. 可视化聚类结果
draw_cluster(dataset=dataset_scaled, centers=cluster_centers, labels=cluster_labels, k=k, title=f'鸢尾花K-means聚类结果(K={k},SSE={sse:.4f})'
)6. K 值选择:如何确定最优簇数
K-means 需预先指定 K 值,若 K 值不合理(如 K=2 或 K=4),会导致聚类效果差。常用肘部法和轮廓系数选择最优 K 值:
(1)肘部法(Elbow Method)
通过计算不同 K 值对应的 SSE,绘制 “K-SSE” 曲线,曲线弯曲的 “肘部” 对应的 K 值即为最优值(此时增加 K 值,SSE 下降幅度显著减小):
# 定义K值范围(1-10,可根据需求调整)
k_range = range(1, 11)
# 存储不同K值的SSE
sse_list = []# 遍历K值,计算SSE
for k_candidate in k_range:kmeans_temp = KMeans(n_clusters=k_candidate, n_init=10, random_state=42)kmeans_temp.fit(dataset_scaled)sse_list.append(kmeans_temp.inertia_) # 记录SSE# 绘制肘部法曲线
plt.figure(figsize=(10, 6))
plt.plot(k_range, sse_list, marker='o', linestyle='-', color='#1f77b4')
# 标记肘部位置(此处K=3)
plt.scatter(3, sse_list[2], color='red', s=200, zorder=5)
plt.annotate('肘部(最优K=3)', xy=(3, sse_list[2]), xytext=(4, sse_list[2]+5),arrowprops=dict(arrowstyle='->', color='red'), fontsize=12)# 添加图表标签
plt.title('K-means肘部法选择最优K值', fontsize=14, pad=15)
plt.xlabel('簇数K', fontsize=12)
plt.ylabel('误差平方和(SSE)', fontsize=12)
plt.xticks(k_range)
plt.grid(linestyle='--', alpha=0.3)
plt.show()肘部法结果解读
- K=1 时,SSE 最大(所有样本归为 1 个簇,簇内差异大);
- K=2 时,SSE 大幅下降(簇内差异减小);
- K=3 时,SSE 下降幅度明显减缓(曲线出现肘部);
- K>3 时,SSE 下降幅度极小(增加簇数对聚类效果提升有限,且可能过拟合);
- 结论:最优 K 值为 3,与鸢尾花真实品种数一致。
(2)轮廓系数(Silhouette Coefficient)
轮廓系数衡量 “样本与自身簇的相似度” 和 “与最近邻簇的相似度”,取值范围 [-1,1],值越接近 1,聚类效果越好:
from sklearn.metrics import silhouette_score# 存储不同K值的轮廓系数
silhouette_scores = []# 遍历K值(K=2开始,因K=1无法计算轮廓系数)
for k_candidate in range(2, 11):kmeans_temp = KMeans(n_clusters=k_candidate, n_init=10, random_state=42)labels_temp = kmeans_temp.fit_predict(dataset_scaled)# 计算平均轮廓系数score = silhouette_score(dataset_scaled, labels_temp)silhouette_scores.append(score)# 绘制轮廓系数曲线
plt.figure(figsize=(10, 6))
plt.plot(range(2, 11), silhouette_scores, marker='o', linestyle='-', color='#2ca02c')
# 标记最大轮廓系数对应的K值(此处K=3)
max_score_idx = np.argmax(silhouette_scores)
best_k_silhouette = range(2, 11)[max_score_idx]
plt.scatter(best_k_silhouette, silhouette_scores[max_score_idx], color='red', s=200, zorder=5)
plt.annotate(f'最大系数(K={best_k_silhouette})', xy=(best_k_silhouette, silhouette_scores[max_score_idx]), xytext=(best_k_silhouette+1, silhouette_scores[max_score_idx]-0.05),arrowprops=dict(arrowstyle='->', color='red'), fontsize=12)# 添加图表标签
plt.title('K-means轮廓系数选择最优K值', fontsize=14, pad=15)
plt.xlabel('簇数K', fontsize=12)
plt.ylabel('平均轮廓系数', fontsize=12)
plt.xticks(range(2, 11))
plt.grid(linestyle='--', alpha=0.3)
plt.show()print(f"\n=== 轮廓系数结果 ===")
print(f"最优K值:{best_k_silhouette}")
print(f"对应平均轮廓系数:{silhouette_scores[max_score_idx]:.4f}")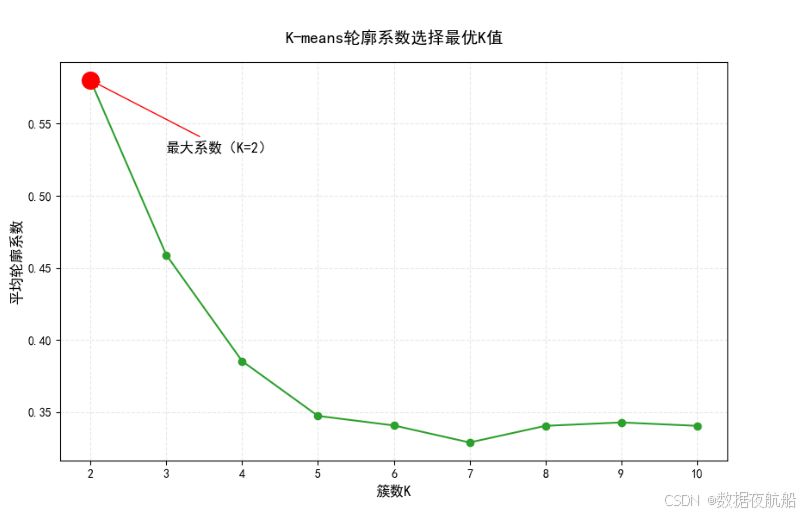
轮廓系数结果解读
- K=3 时,轮廓系数最大(约 0.5-0.6),说明此时簇内相似度高、簇间差异大;
- K=4 时,轮廓系数下降,说明增加簇数导致部分相似样本被拆分,聚类合理性降低;
- 结论:最优 K 值为 3,与肘部法结果一致,验证了 K=3 的合理性。
五、K-means 算法的优缺点与改进方向
1. 优点
- 简单易实现:核心逻辑仅需 “质心迭代 + 距离计算”,代码门槛低;
- 可扩展性强:支持大数据集(通过
sklearn的batch_size参数可处理百万级样本); - 聚类速度快:迭代过程计算量小,收敛速度快;
- 结果易解释:簇中心可对应 “类的典型特征”(如鸢尾花簇中心可解释为某品种的平均形态)。
2. 缺点
- 对初始质心敏感:不同初始质心可能导致不同聚类结果(可通过
n_init=10多次初始化解决); - 需预先指定 K 值:无先验知识时难以确定 K 值(需通过肘部法、轮廓系数辅助);
- 对噪声和离群值敏感:离群值会显著拉高 SSE,甚至导致质心偏移(可通过异常值检测预处理解决);
- 不适用于非球形簇:K-means 基于欧式距离,仅能处理球形分布的簇(非球形簇需用 DBSCAN 等算法)。
3. 改进方向
- 初始质心优化:使用 “K-means++” 算法(
sklearn默认),让初始质心尽可能分散,提升结果稳定性; - 处理离群值:聚类前用箱线图、Z-score 等方法删除离群值;
- 混合数据类型:若数据含分类型特征,可先将其编码(如 One-Hot),再用 K-means 聚类;
- 结合其他算法:先用 PCA 降维减少特征维度,再执行 K-means,提升速度与效果。
👏觉得文章对自己有用的宝子可以收藏文章并给小编点个赞!
👏想了解更多统计学、数据分析、数据开发、机器学习算法、数据治理、数据资产管理和深度学习等有关知识的宝子们,可以关注小编,希望以后我们一起成长!
