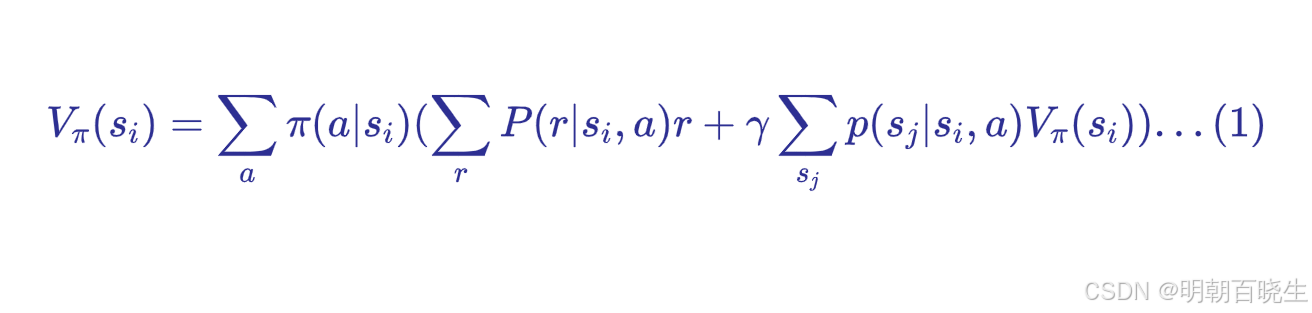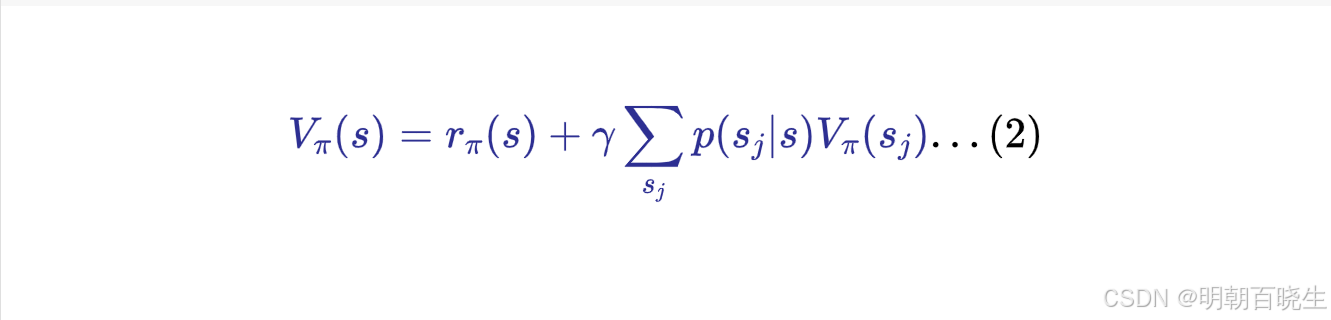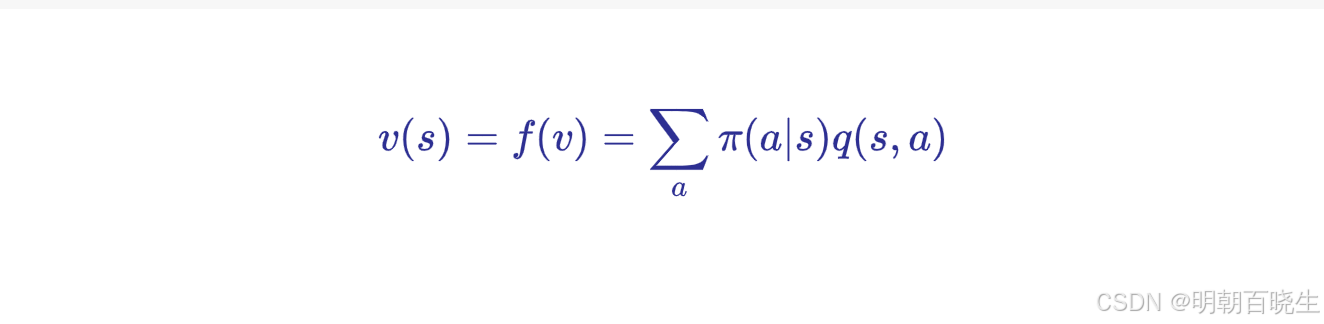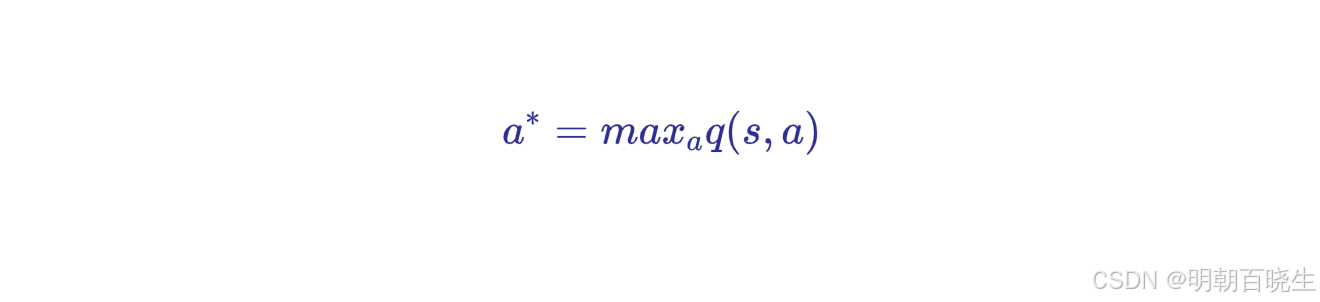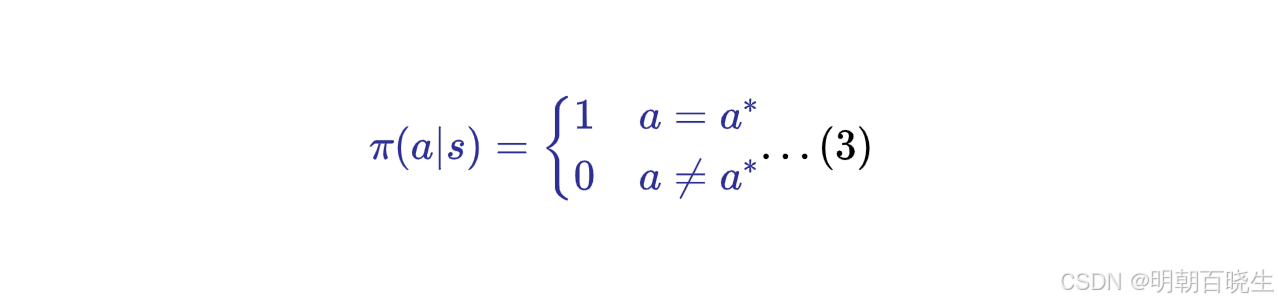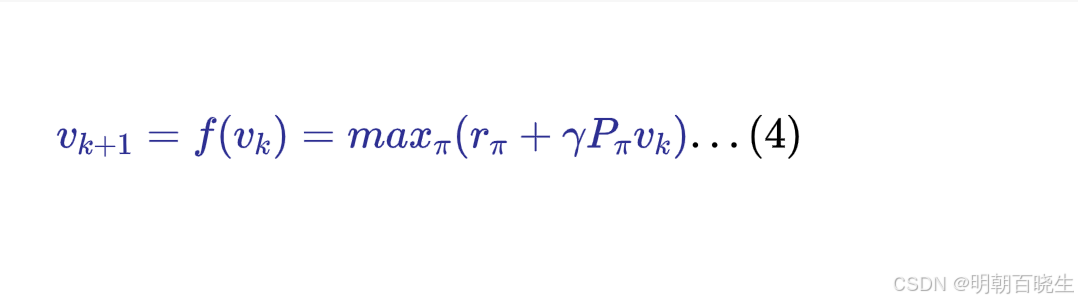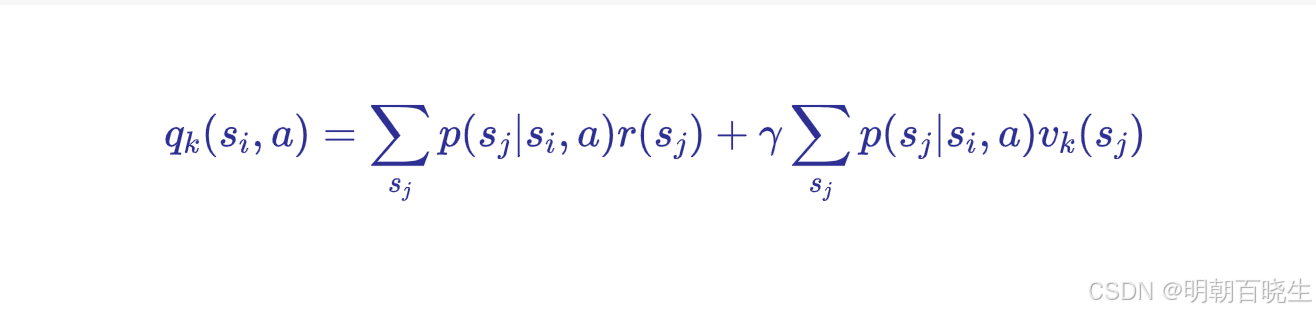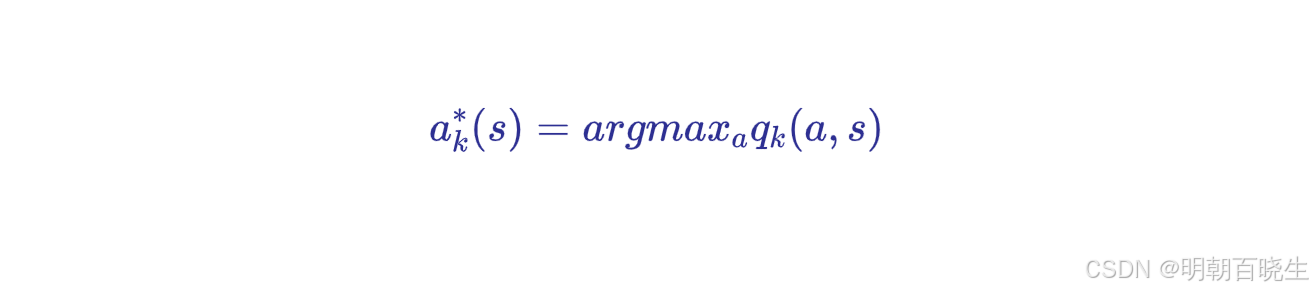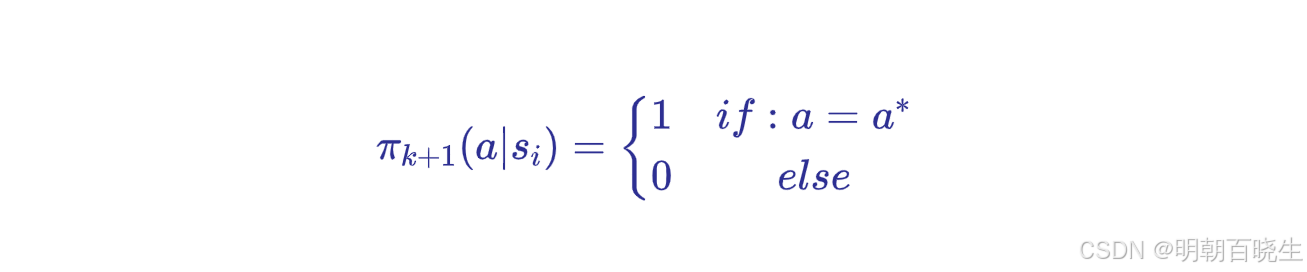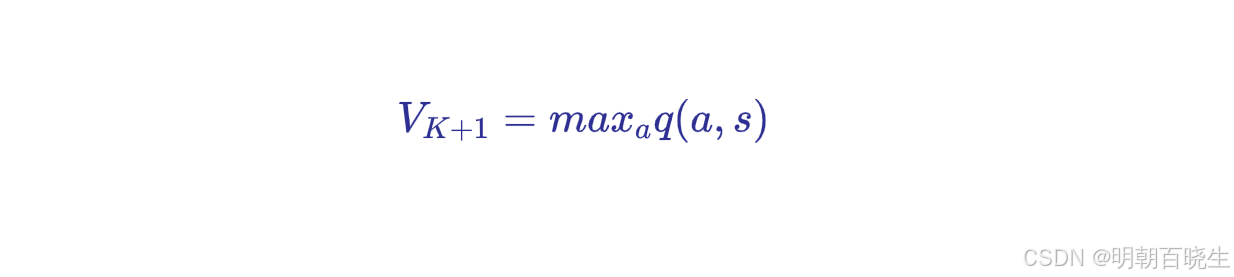当前位置：首页 > news >正文

强化学习【value iterration】【python]

news 2025/9/16 7:40:27

值迭代（Value Iteration）是解决马尔可夫决策过程（MDP）的经典动态规划算法。其核心基于贝尔曼最优性原理，通过迭代方式求解最优价值函数。

Bellman 方程
Bellman 最优方程
值迭代
Python 例子

一 Bellman 方程

1.1 逐元素形式

1.2 矩阵形式

V(s) ：状态 s 的值，表示处于该状态的长期奖励。
r(s,a) ：在状态 s 下采取行动 a所获得的即时奖励。
γ：折扣因子（介于 0 和 1 之间），用于确定未来奖励相对于即时奖励的重要性。
$P(s_j|s)$ 通过采取行动a从状态 s转换到状态 $s_j$ 的概率。
$\pi$ 策略

二 Bellman 最优方程

目的是找到最优策略 $\pi$ 使得状态值V最大

通过contraction mapping 理论,可知道最优状态值可以通过迭代更新求解

Contraction Mapping 理论（压缩映像原理),又称 Banach 不动点定理（Banach Fixed-Point Theorem），是泛函分析和度量空间理论中的核心定理，为研究非线性方程（如代数方程、积分方程、微分方程）的解的存在性与唯一性提供了关键工具。其核心思想是通过构造一个“压缩”的自映射，证明其存在唯一的不动点，并通过迭代法构造性求解。

2.1 最优策略求解

因为
所以

例子：

2.2 最大状态值求解

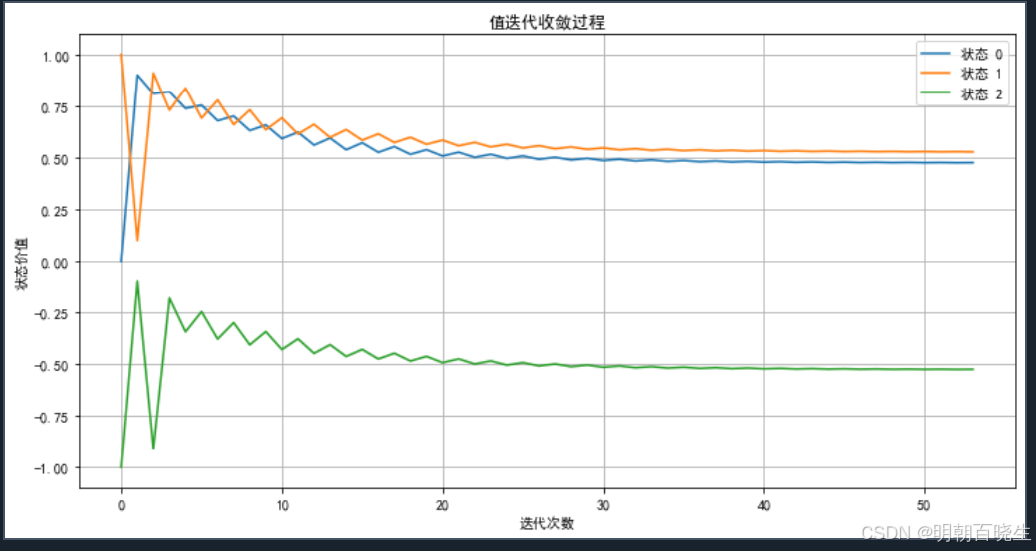
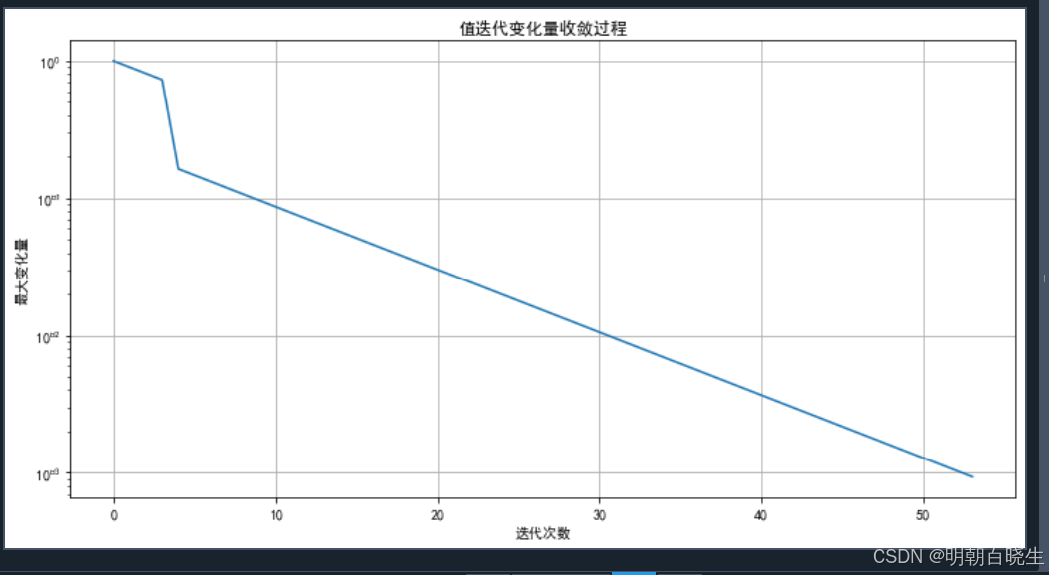
通过迭代更新,最后以指数级收敛（contraction mapping 理论）

三值迭代算法

值迭代算法通过策略更新与值更新两个步骤不断迭代，直至收敛至最优策略。
具体流程如下：

根据当前状态值函数计算各状态-动作对的Q值
采用贪婪策略选择最优动作
依据更新后的策略重新计算状态值函数
重复以上过程直至值函数收敛。

伪代码：值迭代算法

初始化：

已知概率模型 $P(s_j|s_i,a)$ , $r(s_j|s_i,a)$ .初始状态值 $v_0$ .

目标：

寻找最优状态值和一个最优策略,解决贝尔曼最优方程

迭代过程：

当 $v_k$ 在 ∥ $v_k-v_{k-1}$ ∥ 大于一个预定义的小阈值的意义下尚未收敛时，对于第 k 次迭代，执行以下步骤：

对于每一个状态 s∈S

对于每一个动作 a∈A(s)

step1: 执行 Q值计算：

step2 策略更新

step3 值更新
这个算法通过不断迭代更新状态值函数 v 和策略 π，直到值函数收敛，从而找到最优策略

四 Python 例子

# -*- coding: utf-8 -*-
"""
Created on Fri Sep 12 15:36:54 2025@author: chengxf2
""""""
贝尔曼值迭代算法实现
基于马尔可夫决策过程(MDP)的最优价值函数求解
"""import numpy as np
from typing import Dict, List, Tuple
import matplotlib.pyplot as pltSTATE0 = 0
STATE1 = 1
STATE2 = 2  
MOVE_LEFT = 0
MOVE_RIGHT = 1class BellmanValueIteration:"""贝尔曼值迭代算法实现类通过迭代更新状态价值函数，最终收敛到最优价值函数和最优策略基于贝尔曼最优方程: V*(s) = max_a [ R(s,a) + γ * Σ P(s'|s,a) * V*(s') ]"""def __init__(self, states: List[int], actions: List[int], transition_probs: Dict[Tuple[int, int, int], float],rewards: Dict[Tuple[int, int, int], float],gamma: float = 0.95, theta: float = 1e-6):"""初始化值迭代算法Args:states: 状态列表 [0, 1, 2, ..., n-1]actions: 动作列表 [0, 1, 2, ..., m-1]transition_probs: 转移概率字典 {(s, a, s'): probability}rewards: 奖励字典 {(s, a, s'): reward}gamma: 折扣因子，默认0.95theta: 收敛阈值，默认1e-6"""self.states = statesself.actions = actionsself.transition_probs = transition_probsself.rewards = rewardsself.gamma = gamma  # 折扣因子self.theta = theta  # 收敛阈值# 初始化价值函数，所有状态价值为0self.values = {state: 0.0 for state in states}# 存储每次迭代的价值函数变化用于分析self.value_history = []self.delta_history = []def get_transition_info(self, state: int, action: int) -> List[Tuple[int, float, float]]:"""获取给定状态和动作的所有可能转移信息Args:state: 当前状态action: 执行的动作Returns:列表，每个元素为(下一个状态, 转移概率, 即时奖励)"""transitions = []for next_state in self.states:key = (state, action, next_state)if key in self.transition_probs and self.transition_probs[key] > 0:prob = self.transition_probs[key]reward = self.rewards.get(key, 0.0)transitions.append((next_state, prob, reward))return transitionsdef compute_q_value(self, state: int, action: int) -> float:"""计算状态-动作对的Q值Args:state: 当前状态action: 执行的动作Returns:Q(s, a) = Σ P(s'|s,a) * [R(s,a,s') + γ * V(s')]"""q_value = 0.0transitions = self.get_transition_info(state, action)for next_state, prob, reward in transitions:# 贝尔曼方程的核心计算q_value += prob * (reward + self.gamma * self.values[next_state])return q_valuedef value_iteration_step(self) -> float:"""执行一次值迭代更新Returns:本次迭代中价值函数的最大变化量"""max_delta = 0.0  # 记录最大变化量# 创建新的价值函数副本用于批量更新new_values = self.values.copy()for state in self.states:# 保存旧值用于计算变化量old_value = self.values[state]# 计算所有可能动作的Q值q_values = []for action in self.actions:q_value = self.compute_q_value(state, action)q_values.append(q_value)# 贝尔曼最优更新：选择最大Q值作为新的状态价值# 确保有可用的动作if q_values:  new_values[state] = max(q_values)# 更新最大变化量delta = abs(old_value - new_values[state])max_delta = max(max_delta, delta)# 批量更新价值函数self.values = new_valuesreturn max_deltadef solve(self, max_iterations: int = 1000) -> Dict[int, float]:"""执行值迭代算法直到收敛Args:max_iterations: 最大迭代次数，防止无限循环Returns:收敛后的最优价值函数"""print("开始值迭代求解...")iteration = 0while iteration < max_iterations:# 执行一次迭代更新max_delta = self.value_iteration_step()# 记录历史数据用于分析self.value_history.append(self.values.copy())self.delta_history.append(max_delta)# 打印迭代信息if iteration % 10 == 0:print(f"迭代 {iteration}: 最大变化量 = {max_delta:.3f}")# 检查是否收敛if max_delta < self.theta:print(f"在第 {iteration} 次迭代后收敛")breakiteration += 1if iteration == max_iterations:print("达到最大迭代次数，可能尚未完全收敛")return self.valuesdef extract_policy(self) -> Dict[int, int]:"""从最优价值函数中提取最优策略Returns:最优策略：每个状态对应的最优动作"""policy = {}for state in self.states:best_action = Nonebest_value = float('-inf')# 对每个动作计算Q值，选择最大的for action in self.actions:q_value = self.compute_q_value(state, action)if q_value > best_value:best_value = q_valuebest_action = actionpolicy[state] = best_actionreturn policydef plot_convergence(self):"""绘制价值函数收敛过程"""plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号if not self.value_history:print("没有收敛历史数据")returnplt.figure(figsize=(12, 6))# 绘制每个状态的价值收敛过程for state in self.states:state_values = [v[state] for v in self.value_history]plt.plot(state_values, label=f'状态 {state}')plt.xlabel('迭代次数')plt.ylabel('状态价值')plt.title('值迭代收敛过程')plt.legend()plt.grid(True)plt.show()# 绘制最大变化量的收敛过程plt.figure(figsize=(12, 6))plt.plot(self.delta_history)plt.xlabel('迭代次数')plt.ylabel('最大变化量')plt.title('值迭代变化量收敛过程')plt.yscale('log')  # 使用对数坐标更好地显示收敛plt.grid(True)plt.show()# 示例：简单的3状态MDP问题
def create_example_mdp():"""创建一个简单的3状态MDP示例状态: 0, 1, 2动作: 0 (左), 1 (右)状态2是终止状态，奖励为+1"""states =  [STATE0, STATE1, STATE2]actions = [MOVE_LEFT, MOVE_RIGHT]  # 0: 向左, 1: 向右# 初始化转移概率和奖励字典transition_probs = {}rewards = {}#state,action, new_state=1# 状态0：向左移动到状态0，向右移动到状态1transition_probs[(STATE0, MOVE_LEFT, STATE0)] = 1.0  # 向左移动，保持在状态0transition_probs[(STATE0, MOVE_RIGHT, STATE1)] = 1.0  # 向右移动，到状态1rewards[(STATE0, MOVE_LEFT, STATE0)] = 0.0rewards[(STATE0, MOVE_RIGHT, STATE1)] = 0.0# 状态1：向左移动到状态0，向右移动到状态2transition_probs[(STATE1, MOVE_LEFT, STATE0)] = 1.0  # 向左移动，到状态0transition_probs[(STATE1, MOVE_RIGHT, STATE2)] = 1.0  # 向右移动，到状态2rewards[(STATE1, MOVE_LEFT, STATE0)] = 0.0rewards[(STATE1, MOVE_RIGHT, STATE2)] = 1.0  # 到达终止状态获得奖励# 状态2是终止状态，所有动作都保持在状态2transition_probs[(STATE2, MOVE_LEFT, STATE1)] = 1.0transition_probs[(STATE2, MOVE_RIGHT, STATE2)] = 1.0rewards[(STATE2, MOVE_LEFT, STATE1)] = -1.0rewards[(STATE2, MOVE_RIGHT, STATE2)] = -1.0return states, actions, transition_probs, rewardsdef main():"""主函数：演示值迭代算法的使用"""# 创建示例MDPstates, actions, transition_probs, rewards = create_example_mdp()# 初始化值迭代算法vi = BellmanValueIteration(states=states,actions=actions,transition_probs=transition_probs,rewards=rewards,gamma=0.9,      # 折扣因子theta=1e-3      # 收敛阈值)# 执行值迭代求解optimal_values = vi.solve(max_iterations=300)# 输出最优价值函数print("\n最优价值函数:")for state, value in optimal_values.items():print(f"V*(STATE{state}) = {value:.4f}")# 提取并输出最优策略optimal_policy = vi.extract_policy()print("\n最优策略:")for state, action in optimal_policy.items():action_name = "向左" if action == 0 else "向右"print(f"状态 {state} -> {action_name}")# 绘制收敛过程vi.plot_convergence()# 验证贝尔曼最优方程print("\n验证贝尔曼最优方程:")for state in states:# 计算当前状态的贝尔曼最优更新q_values = []for action in actions:q_value = vi.compute_q_value(state, action)q_values.append(q_value)print(f"Q({state}, {action}) = {q_value:.4f}")# 检查是否满足 V*(s) = max_a Q(s,a)max_q = max(q_values) if q_values else 0print(f"V*({state}) = {optimal_values[state]:.4f}, max_a Q(s,a) = {max_q:.4f}")print(f"一致性检查: {'通过' if abs(optimal_values[state] - max_q) < 1e-3 else '失败'}")print("-" * 40)if __name__ == "__main__":# 设置随机种子确保可重复性np.random.seed(42)# 运行主程序main()