当前位置：首页 > news >正文

力扣：1547. 切棍子的最小成本

news 2025/9/16 7:40:25

有一根长度为 n 个单位的木棍，棍上从 0 到 n 标记了若干位置。例如，长度为 6 的棍子可以标记如下：

给你一个整数数组 cuts ，其中 cuts[i] 表示你需要将棍子切开的位置。

你可以按顺序完成切割，也可以根据需要更改切割的顺序。

每次切割的成本都是当前要切割的棍子的长度，切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍（这两根木棍的长度和就是切割前木棍的长度）。请参阅第一个示例以获得更直观的解释。

返回切棍子的 最小总成本 。

示例 1：

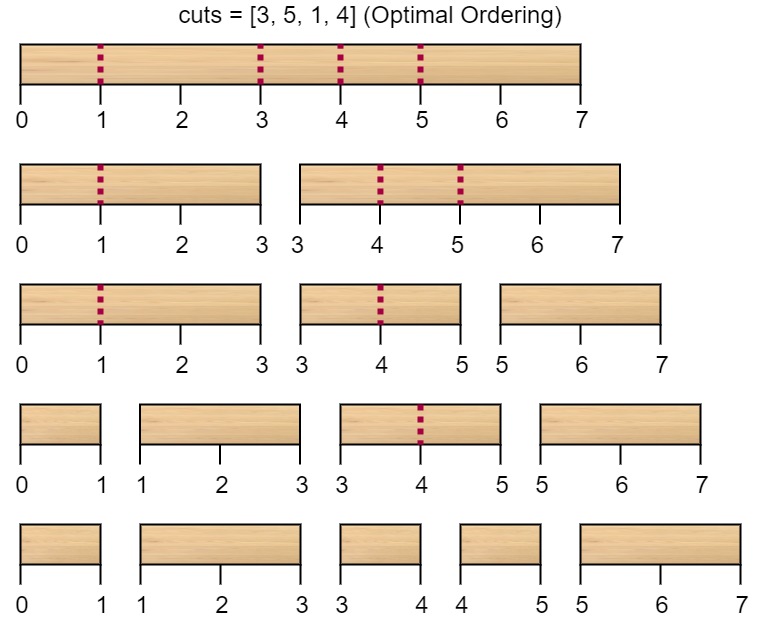
输入：n = 7, cuts = [1,3,4,5]
输出：16
解释：按 [1, 3, 4, 5] 的顺序切割的情况如下所示：

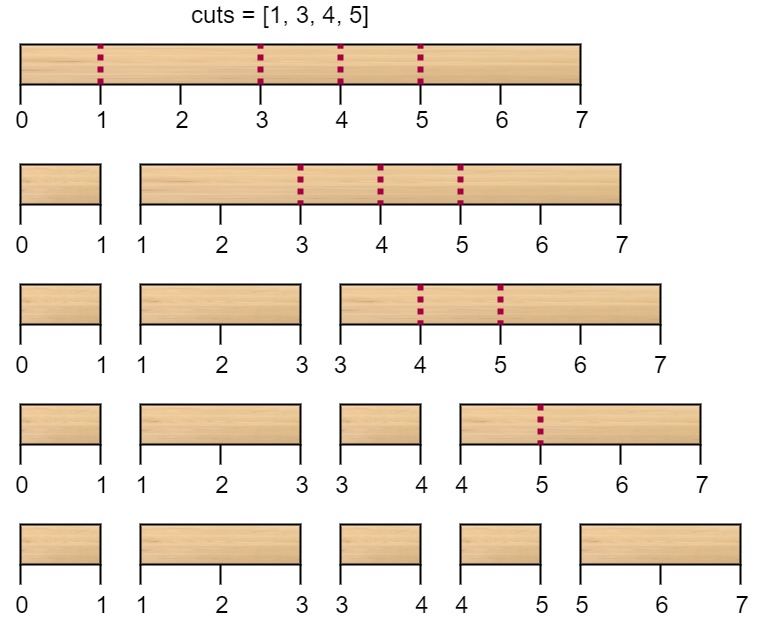
第一次切割长度为 7 的棍子，成本为 7 。第二次切割长度为 6 的棍子（即第一次切割得到的第二根棍子），第三次切割为长度 4 的棍子，最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后，总成本 = 16（如示例图中 7 + 4 + 3 + 2 = 16）。

示例 2：

输入：n = 9, cuts = [5,6,1,4,2]
输出：22
解释：如果按给定的顺序切割，则总成本为 25 。总成本 <= 25 的切割顺序很多，例如，[4, 6, 5, 2, 1] 的总成本 = 22，是所有可能方案中成本最小的。

区间dp，考虑每个端点的切割情况

首先要知道，当前切割成本就是当前切割木棍的长度为左断点的前一个断电位置与右断点后一个断点位置之间的距离

之后开始切割木棍，对于任意一个切割区间 [ l,r ]，（l,r为切割的2个断点在数组中的下标），要选在其中寻找哪个点进行切割，于是就要遍历区间，如果当前的切割点为 i，那么在 i 处切割后，切割区间 [ l,r ]就出现了2个子区间切割区间 [ l,i-1 ]和切割区间 [ i+1,r ]，这时就需要递归访问2个子区间，在子区间上再求最小成本

这里只给出了记忆化搜索的代码，后续可改成dp表将在时间和空间上进一步得到优化

AC代码：

C++版：


class Solution {
public:int fun(int l, int r, vector<int>& a, vector<vector<int>>& dp) {//l,r为切割的2个断点在a数组中的下标if (l > r) {return 0;}if (dp[l][r]) {return  dp[l][r];}int val = a[r + 1] - a[l - 1];//当前切割成本//当前切割木棍的长度为左断点的前一个断电位置与右断点后一个断点位置之间的距离if (l == r) {return val;}else {int ans = 0x3f3f3f3f;for (int i = l;i <= r;i++) {//找切割点ans = min(ans, fun(l, i - 1, a, dp) + fun(i + 1, r, a, dp) + val);}dp[l][r] = ans;return dp[l][r] ;}}int minCost(int n, vector<int>& cuts) {vector<int> a = cuts;a.push_back(0);sort(a.begin(), a.end());a.push_back(n);vector<vector<int>> dp(a.size() + 1, vector<int>(a.size() + 1));return fun(1, a.size() - 2, a,dp);}
};

java版：

import sun.jvm.hotspot.oops.Array;import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;class Solution {public int fun(int l,int r,ArrayList<Integer> a,int[][] dp){if(l>r){return 0;}if(dp[l][r]!=-1) {return dp[l][r];}int val=a.get(r+1)-a.get(l-1);int ans=10000000;for(int i=l;i<=r;i++){ans=Math.min(ans,fun(l,i-1,a,dp)+fun(i+1,r,a,dp)+val);}dp[l][r]=ans;return ans;}public int minCost(int n, int[] cuts) {ArrayList<Integer> a = new ArrayList<>();a.add(0);a.add(n);for (int i : cuts) {a.add(i);}Collections.sort(a);final int len = a.size()+10;int[][] dp=new int[len][len];for (int i = 0; i < len; i++) {Arrays.fill(dp[i], -1);}return fun(1,a.size()-2,a,dp);}
}